Príklad 2.1.4

Grafická závislosť dráhy guličky ako funkcia času je znázornená na obrázku. Určite: a) smer pohybu guličky; b) časovú závislosť polohového vektora guličky; c) rýchlosť guličky  v bodoch A a B; d) priemernú rýchlosť  guličky; e) zrýchlenie guličky.

Riešenie: a) Z grafu je zrejmé, že pohyb prebieha v smere osi x . Polohový vektor guličky   v každom časovom okamihu  t  je určený rovnicou   r = r (t) =  x(t) i . Gulička sa pohybuje po priamke určenej jednotkovým vektorom i.  Trajektóriou pohybu je priamka ležiaca v smere osi x.

 

b) Časovú závislosť polohového vektora určíme z grafu tak, že určíme  smernicu priamky  k závislosti súradnice x =  x(t )= kt , kde

 

    

 

     Polohový vektor guličky je určený rovnicou   r = r (t) =  x(t) i = kt i = 0,5 t i.

 

c) Rozmer [ m.s^-1] smernice priamky  x =  x(t) naznačuje jej fyzikálny význam. Smernica priamky, resp. tg a  určuje okamžitú rýchlosť guličky v danom bode grafu.  Táto je rovnaká pre všetky body grafu a je určená  rovnicou

 

v = v (t) =  v_x(t) i  = 0,5 i

 

Veľkosť rýchlosti guličky v bodoch A i B je rovnaká a rovná sa  0,5  m.s^-1

 

d) Nakoľko ide o pohyb rovnomerný priemerná rýchlosť  guličky sa rovná jej okamžitej rýchlosti  v_p   = v_x = 0,5  m.s^-1

 

e) Zrýchlenie guličky     ,  pretože rýchlosť pohybu sa nemení.

 

Príklad 2.1.5

Dievča vykročilo  po priamej ulici v smere juh - sever. Graf jej závislosti vzdialenosti od domu ako funkcia času t je znázornený na  obrázku. Kvalitatívne a kvantitatívne  vyhodnoťte,  akým pohybom  sa dievča pohybuje v jednotlivých časových intervaloch a zistite:

a) priemernú rýchlosť dievčaťa počas prvej polovice celkového  časového intervalu;

            b) priemernú rýchlosť v siedmej  a štrnástej  minúte pohybu;

            c) priemernú rýchlosť dievčaťa  počas celého časového intervalu znázorneného na grafe.

 

 

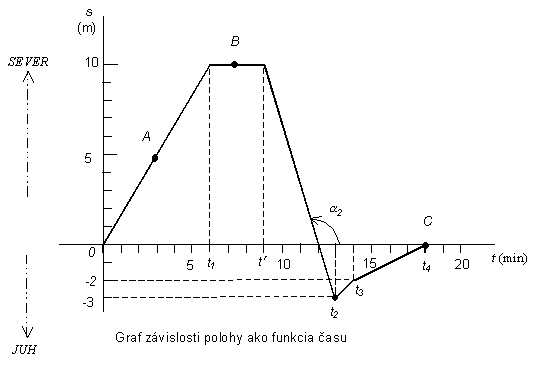
Riešenie: Kvalitatívne hodnotenie možno uskutočniť úvahou:  V každom časovom intervale poloha dievčaťa je lineárnou funkciou času s rôznou smernicou, resp. sklonom priamky.  To znamená, že dievča sa pohybuje rovnomerným pohybom s rôznymi rýchlosťami. Najrýchlejšie pôjde v tom časovom intervale, v ktorom smernica priamky, resp. tg a  je najväčší (<t₂, t¢>). Ak je priamka rovnobežná s časovou osou,  zmena polohového vektora dievčaťa  sa rovná nule, t.j. dievča oddychuje v kľude. Záporná hodnota smernice určuje zmenu smeru pohybu.  Presvedčíme sa o tom  kvantitatívne. V intervale Dt₁ = t₁ – t₀  je   v₁  = Ds / Dt₁ = (10/360)  m.s^-1 = 0,027  m.s^-1  . V intervale  Dt₂  = t´  – t₁  je   v ₂ = 0  m.s^-1. V intervale Dt₃ = t₂  – t´  je v₃ = tg a ₂  = (- 10 /180)  m.s^-1 = - 0,055  m.s^-1 (dievča sa obrátilo a kráča rýchlejšie ako doteraz smerom na juh). V intervale Dt₄ = t₃  – t₂   v₄  = - 0,016  m.s^-1 . V intervale Dt₅ = t₄  – t₃    v₅ = (2/240) m.s^-1 = 0,008 m.s^-1 smerom z juhu na sever. V časovom okamihu t₄  =18 min = 1080 s sa   dievča opäť nachádza na mieste, z ktorého  vyšlo.

a) Označme D t´ dĺžku   časového intervalu < 0, t¢ >, kde  t´= 9 min, t.j.  polovica z celkového doby pohybu t₄ = 18 min, určeného  z grafu. Nech < 0, t¢ >  je súčtom  dvoch  intervalov < 0, t₁ > a  < t₁, t₂> ,

ktorých dĺžka je D t ´=D t₁ + D t_{2 .}  Z grafu  určíme číselné hodnoty   D t ´=   9 min = 540  s, D t₁ = 6 min = 360 s a D t₂ = 3 min = 180 s. Priemernú rýchlosť určíme zo vzťahu

 

 

kde s₁ je dĺžka dráhy, ktoré dievča prešlo za časový interval   < 0, t₁ >   a  s₂  je dĺžka dráhy, ktoré dievča prešlo za časový  interval < t₁, t₂> _.  Z grafu vidíme, že s₂  = 0 (dievča oddychovalo). Veľkosť priemernej  rýchlosti  v prvej polovici časového intervalu vypočítame po dosadení

 

 

b)     Z grafu  je zrejmé, že počas siedmej minúty rýchlosť dievčaťa bola nulová , t.j.  v_p7 = 0 m.s^-1. Tento výsledok možno určiť i zo skutočnosti, že  zmena polohového vektora  počas siedmej minúty je nulová. Rýchlosť počas štrnástej minúty určíme z grafu

 

 

 

c)     Priemernú rýchlosť dievčaťa  za celkový čas pohybu t je nula, pretože vektor posunutia v časovom intervale t₄ – t ₀    sa rovná nule.

 

Príklad 2.1.6

Určite okamžité rýchlosti  objektu v bodoch  A ,V a M, ak časová závislosť  pohybu v smere osi x je určená grafom na obrázku.

 

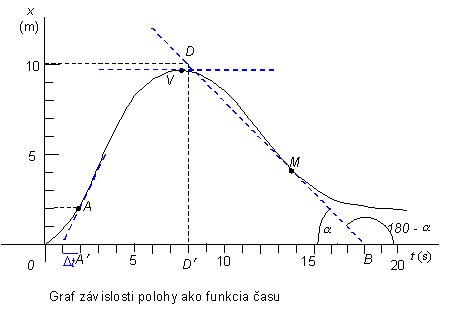
Riešenie:

 Keďže nemáme zadanú exaktnú rovnicu závislosti  x ako funkciu času t, nemôžeme dať precíznu odpoveď, pretože  nepoznáme  (dx / dt )_A resp. v bodoch V a M.  Odpovedať na otázku  nám pomôže nákres dotyčnice  ku grafu funkcie v danom bode. Smernica dotyčnice v tomto bode  určuje okamžitú rýchlosť  objektu v skúmanom bode grafu.

 

 

Po číselnom dosadení hodnôt odčítaných z grafu dostaneme  v _A = 2 ms^-1.

Bod  V je maximom funkcie x = x(t).  Dotyčnica v tomto bode je rovnobežná s  časovou osou,  t.j. smernica resp. derivácia funkcie v bode V sa rovná nule . Objekt sa v bode V zastaví.

 

 

Obdobne určíme okamžitú rýchlosť v bode M z trojuholníka B D D¢.

 

. 

 

 

Záporné znamienko hovorí, že objekt sa pohybuje v zápornom smere osi x .

 

 

 

Príklad 2.1.7

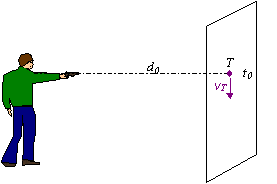
Na strelnici v lunaparku chce strelec zasiahnuť nábojom  vystreleným z pušky  pohyblivý terč T. Predpokladajme, že náboj  sa pohybuje rovnomerným priamočiarym pohybom  s  rýchlosťou v_n = 50 m.s^-1. Terč v okamihu výstrelu sa nachádza vo vertikálnej rovine v bode T vo  vzdialenosti  d₀ = 3 m od strelca a pohybuje sa kolmo na túto spojnicu rovnomerným priamočiarym  pohybom rýchlosťou v_T = 20 m.s^-1.  Zistite, či strelec zasiahol terč, ak mieril pod uhlom 30 ⁰ od  horizontálnej roviny ( viď obrázok).

 

 

 

 

 

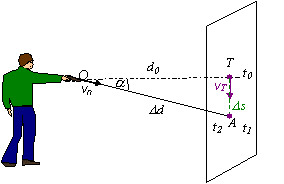
Riešenie:

Aby strelec trafil terč, musí sa  terč i strela  v určitom časovom okamihu t   nachádzať na rovnakom mieste, ktoré označíme A.  Nech sa terč   z bodu T do bodu A dostane za časový interval  D t₁ = t₁ – t₀

(t₀ = 0 ) a za tento  interval prebehne dĺžku dráhy  Ds, určenej rovnicou

 

                                                                                                (a)                                 

 

Z obrázku pre miesto zásahu  platí

 

                                                                                (b)

 

Dobu letu terču určíme, ak dosadíme rovnicu (b)   do (a)

 

 

Označme t₂ dobu letu  náboja z bodu O do bodu  A.  Za túto dobu náboj  preletí  dĺžku dráhy Dd, pre ktorú platí

 

 .

 

Na základe  Pytagorovej  vety  a po dosadení za Dd,  určíme časový interval t₂ potrebný  na doletenie náboja do bodu A.

 

 

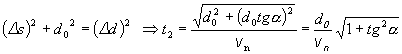
Ak náboj i terč doletia do bodu A za rovnaký časový interval,  strelec trafí terč. Po dosadení číselných hodnôt dostávame pre

 

 

 

 

 

Získané  číselné hodnoty sú rôzne, takže strelec nezasiahol pohyblivý terč.

 

Príklad 2.1.8

Raketa sa z pokoja začala pohybovať v kladnom smere osi x  tak, že jej zrýchlenie pri priamočiarom pohybe rovnomerne   rastie s  časom.  Za  prvých  5  sekúnd pohybu   jej   zrýchlenie   vzrástlo z nulovej hodnoty na  hodnotu a₁ = 5 m.s^-2. Za predpokladu, že vplyv prostredia na pohyb rakety zanedbáte, určite:

a) funkčnú závislosť zrýchlenia rakety od času a smer, v ktorom  pohyb prebieha;

b) funkčnú závislosť jej rýchlosti od času;

c)  funkčnú závislosť prebehnutej dráhy od času;

d) rýchlosť, ktorú dosiahla raketa  za pol minúty svojho pohybu;

e) dráhu, ktorú za tento čas raketa preletela. 

 

Riešenie:

            Zo zadania príkladu si vypíšeme veličiny a ich hodnoty, ktoré príklad udáva a tiež veličiny, ktoré máme určiť:

v₀ = v(0)  =  0 m.s^-1

t₁ = 5 s

a₁ = 5 m.s^-2

t₂ = 0,5 min = 30 s

v = v(t) = ?

s = s(t) = ?

v = v(t₂) = ?

s = s(t₂) = ?

 

a) Určíme funkčnú závislosť zrýchlenia rakety od času pri tomto priamočiarom pohybe.

 Prvá veta príkladu  nám hovorí, že strela sa dáva do pohybu takým spôsobom, že jej zrýchlenie pri priamočiarom pohybe  rovnomerne rastie s časom. Graficky túto skutočnosť môžeme znázorniť priamkou a matematicky formulovať rovnicou priamky, ktorá je v súradnicovom systéme xy vyjadrená rovnicou y = kx + q.  V nami vyšetrovanom prípade nezávisle premennou je čas t a závisle premennou zrýchlenie a . Preto pri transformácii súradníc  x® t  a  y ® a ,  zvážení, že na počiatku deja t₀ = 0 s raketu umiestnime do počiatku súradnicového systému, t. j. q = 0, časová závislosť zrýchlenia  bude daná vzťahom

 

a  = a (t)  = a (t) i

 

kde i  je jednotkový vektor v smere pohybu rakety po priamke. Pre časovú závislosť veľkosti zrýchlenia nám platí

 

a = a (t) = kt

 

Konštantu priamej úmernosti k, resp. smernicu tejto priamky ( tg  a = k),  určíme zo zadaných hodnôt t₁  a zrýchlenia  a(t₁) :

 

 

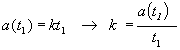
Po dosadení číselných hodnôt dostávame

 

 

 

b) Určime funkčnú závislosť rýchlosti od času pri tomto pohybe:

Keďže sa jedná o  pohyb po priamke,  počas celého pohybu bude ležať i vektor rýchlosti v i polohový vektor  strely r v smere vektora zrýchlenia a, t.j. v smere určeným jednotkovým vektorom i_,  čo zapíšeme

 

 v  = v i,   r  = x i

 

Nakoľko smer vektorov a, v a r    sme si už určili, vektorové veličiny nemusíme v ďalšom uvažovať vo vektorovom tvare a môžeme ich písať len v skalárnom tvare. To znamená, že sa vlastne budeme zaujímať už len o veľkosť daných vektorových veličín. Potom

 

                  

                   

 

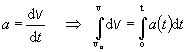
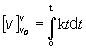
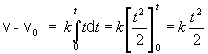
Počiatočná rýchlosť v₀  strely je nulová, takže pre hľadanú funkčnú závislosť veľkosti rýchlosti od času dostávame vzťah

                       (a)

Pre vektor rýchlosti, na základe vyššie určeného smeru pohybu, možno písať

 

 

c) Určime funkčnú závislosť prebehnutej dráhy od času pri tomto priamočiarom pohybe:

 

Funkčnú závislosť dráhy od času určíme z definície rýchlosti

 

 

 

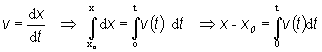
Nakoľko sme strelu  umiestnili na počiatku deja do počiatku súradnicového systému  x₀ = 0.

Pre veľkosť prebehnutej dráhy dostávame

 

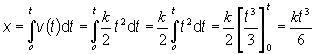                     (b)

 

Hľadanú funkčnú závislosť polohového  vektora r možno zapísať

 

 

d) Určime akú rýchlosť dosiahla strela  za pol minúty svojho pohybu:

Z vypočítanej závislosti rýchlosti od času určenej rovnicou (a)

po dosadení uvedených číselných hodnôt dostaneme

 

 

e) Určime,  akú dráhu za tento čas strela prešla:  Z vypočítanej závislosti dráhy od času (rovnica (b)),

po dosadení uvedených číselných hodnôt, dostaneme