2.1 Kinematika hmotného bodu

 

2.1.1 Základné kinematické pojmy a veličiny

            Pri skúmaní pohybu je nevyhnutné si zvoliť vzťažnú sústavu. V praxi často sa stretávame so  vzťažnou sústavou, ktorú tvorí určitá súradnicová sústava. Veľmi často využívame tzv. karteziánsku pravouhlú súradnicovú sústavu, určenú začiatkom O (vzťažným bodom), do ktorého sú umiestnené tri navzájom kolmé jednotkové vektory i, j, k v smere súradnicových osí x, y, z, respektíve. Vzhľadom na takúto súradnicovú sústavu polohu skúmaného bodu A (obr. 2.1.1)  máme určenú  vtedy, ak poznáme všetky tri jeho súradnice:  x, y, a z  (x je kolmá vzdialenosť bodu A od roviny preloženej osami y a z , ...).

Na určenie polohy  hmotného bodu v priestore vzhľadom na vzťažný bod možno použiť polohový vektor  r.  Polohový vektor bodu A je vektor, ktorého začiatok je vo vzťažnom bode O a koncový bod je v bode A .V karteziánskej súradnicovej sústave polohový vektor r  možno určiť  vzťahom

 

r =  xi + yj + zk                                                                                                        (2.1.1)

 

kde x, y, a z sú súradnice bodu A  a r_x = xi, r_y = yj a r_z  = zk sú zložky vektora r  v smere súradnicových osí.. Veľkosť polohového vektora | r |   je určená rovnicou

 

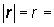
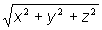                                                                                            (2.1.2)

 

 

 

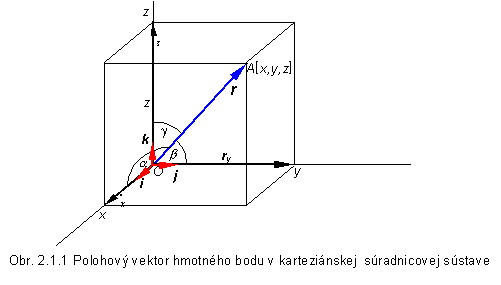
Polohový vektor r  bodu A zviera so súradnicovými osami x, y a z uhly a, b  a g , ktoré nazývame smerové uhly.  Pre smerové kosínusy týchto uhlov platí

 

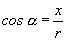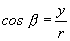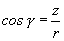;         ;     ;                                                              (2.1.3)

 

 cos² a  + cos² b + cos² g = 1                                                                                   (2.1.4)

 

Kosínusy týchto smerových uhlov,  možno pri znalosti veľkosti polohového vektora r použiť  tiež na určenie súradníc bodu A = [x,y,z].

            Polohu bodu v priestore taktiež často určujeme pomocou  veľkosti polohového vektora  r a dvoch uhlov  j  a 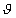 v sférickej (guľovej) súradnicovej sústave  (obr. 2.1.2). Súradnica j  je uhol, ktorý zviera priemet polohového vektora r¢  (sprievodiča) do  roviny  xy s osou x.

 

 

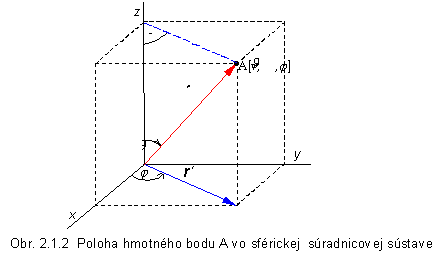
Uhol j  môže nadobúdať hodnoty od 0 ⁰ do 360 ⁰ resp. 0 - 2p. Súradnica J  je uhol, ktorý zviera sprievodič r s osou z (polárnou osou). Môže nadobúdať hodnoty od  0 do p. Súvis medzi karteziánskymi súradnicami x, y, a z  a  sférickými (guľovými) súradnicami r, j   a J, ako vidieť z obrázka 2.1.2,   je určený rovnicami

 

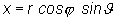
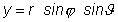                                                                                                    (2.1.5)

 

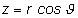
            Ak sa bod vzhľadom na zvolený vzťažný bod nepohybuje, ostáva jeho polohový vektor r vzhľadom na vzťažný bod konštantný.  Znamená to, že sa nemení ani jeho absolútna hodnota, ani jeho smer.

__________________________________

Príklad 2.1.1

V uhlopriečke kvádra leží polohový vektor  r  so začiatkom v bode O a koncovým bodom v bode A.  Určite súradnicepolohového vektora r  vzhľadom na bod  O  v karteziánskej súradnicovej sústave ak poloha bodu A  je určená v sférickej súradnicovej sústave súradnicami

 

A = [r,q,j] = [ 2, 30⁰, 45⁰ ]

 

Riešenie: Karteziánske súradnice bodu A = [x, y, z ] určíme na základe  ich súvisu s sférickými súradnicami z rovníc 2.1.5. Po dosadení číselných hodnôt dostaneme

 

 

 

 

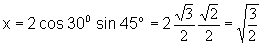
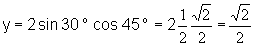
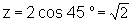
Bod  A má v karteziánskej súradnicovej sústave  súradnice

 

_{_____________________________________________________________}

 

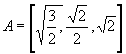
            Pohyb je prebiehajúca zmena vzájomnej polohy vždy aspom dvoch telies. Pri pohybe bodu sa jeho polohový vektor s časom mení  r =r (t) a jeho koncový bod vytvára trajektóriu  (čiaru pohybu), ktorá vo všeobecnosti je priestorová. Pri pohybe hmotného bodu sa mení jeho poloha vzhľadom na vzťažný bod a vo všeobecnosti sa mení veľkosť i smer polohového vektora. Môže nastať špeciálny  prípad, keď  sa:

·       mení len smer polohového vektora pohybujúceho sa bodu, bod ostáva na povrchu gule s polomerom, ktorý sa rovná konštantnej absolútnej hodnote polohového vektora;

·       mení len veľkosť polohového vektora pohybujúceho sa hmotného bodu, bod sa pohybuje po polpriamke;

 

  Pohyb hmotného bodu je úplne určený vtedy, ak v každom časovom okamihu t  sú známe jeho súradnice, čiže ak poznáme funkcie závislosti  súradníc od času

 

x = f₁(t)    ;       y = f₂(t)   ;      z  = f₃(t)                                                                    (2.1.6)

 

Tieto tri skalárne rovnice môžeme zapísať do jednej vektorovej rovnice, takže pohyb   hmotného bodu v priestore je určený i jednou  vektorovou rovnicou

 

 r = f(t)                                                                                                                     (2.1.7)

 

Pri skúmaní pohybu hmotného  bodu v čase a v priestore môžeme rozlišovať pohyb z dvoch hľadísk:

a) z hľadiska  tvaru trajektórie (čiary pohybu , dráhy )

           b) z hľadiska  zmeny rýchlosti pohybujúceho sa hmotného bodu za jednotku času, čiže  podľa zrýchlenia .

(Poznámka: Na strednej škole ste sa stretli s pojmom dráha hmotného bodu. V rôznych učebniciach je možné stretnúť sa s pojmami : trajektória, čiara pohybu, krivka pohybu, ... ako objekt. Tieto pojmy sú synonymá, t.j. slová rovnakého významu. V našom texte budeme používať niektoré z nich.  Musíme si ale uvedomiť, že pre mieru ktorejkoľvek z nich, t.j. mieru trajektórie, resp. čiary pohybu, resp. krivky pohybu, resp. dráhy sa používa pojem  dĺžka dráhy, ktorú  budeme  označovať Ds=s-s₀ (rovnako pre všetky). To znamená, že Ds značí dĺžku dráhy prebehnutej pohybujúcim sa bodom (časticou), meranú od ľubovolného bodu na čiare pohybu. V prípade, ak  na začiatku skúmania hmotný bod (častica) v začiatku súradnicovej sústavy, t.j. s₀ = 0  , možno sa stretnúť s označením pre dĺžku dráhy i  Ds=s .

odľa tvaru trajektórie delíme pohyb na:

1)     priamočiary 

2)     krivočiary

 

Podľa  zmeny veľkosti rýchlosti za jednotku času delíme pohyb  na: 

1)  rovnomerný

2)  nerovnomerný

Aby sme mohli jednotlivé mechanické pohyby kvalitatívne rozlíšiť a kvantitatívne hodnotiť, zavedieme si základné kinematické veličiny rýchlosť a zrýchlenie.

                       

·       Stredná rýchlosť a okamžitá rýchlosť

            Uvažujme pohyb bodu vzhľadom na zvolený vzťažný bod O. V určitom časovom okamihu t₀ sa hmotný bod nachádza v bode A  určenom  polohovým vektorom r₀ a v časovom okamihu  t  v bode B   určenom  polohovým vektorom  r  (obr. 2.1.3). Nech v  časovom intervale Dt = t - t₀  prejde hmotný bod z miesta A do miesta B po trajektórii (krivke pohybu) dráhu, ktorej dĺžka je Ds.

 

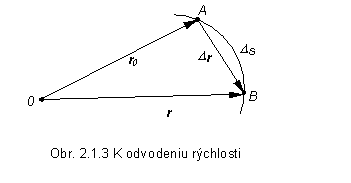
Strednou rýchlosťou v_s pohybujúceho sa hmotného bodu vo zvolenom časovom intervale Dt nazývame podiel

 

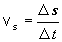                                                                                                                  (2.1.8)

 

Označme rozdiel vektorov  r -r₀  = Dr. Ak budeme zmenšovať časový interval Dt (t.j. bod B budeme voliť stále bližšie a bližšie k bodu A) potom  veľkosť vektora Dr, označuje sa |Dr |,  sa bude stále viac blížiť k dĺžke dráhy Ds prebehnutej skúmaným bodom A. Stredná rýchlosť v_s  pohybujúceho sa bodu sa rovná zmene polohového vektora |Dr | prepočítaného na jednotku času. Je zrejmé, že limitný prípad Dt® 0

 

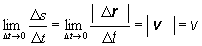                                                                               (2.1.9)

 

určuje veľkosť  okamžitej rýchlosti  v  v čase t. Hraničná hodnota podielu Ds /Dt  pre hodnotu Dt 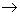 0, resp. derivácia polohového vektora podľa času, volá sa  okamžitá rýchlosť v a  definujeme ju  rovnicou  

 

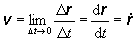                                                                                                (2.1.10)

 

                       

Poznámka: V limitnom prípade t ® 0   | r | =s,  t.j.   | dr | = ds. Veličiny, ds, dt, ...  nazývame infinitezimálnymi alebo elementárnymi, ds - elementárnou dĺžkou  resp. dt - elementárnym časovým úsekom. Vo fyzike je dohoda označovať podiel dr / dt  tiež 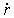, ktorý znamená, že sa jedná o časovú deriváciu polohového vektora. (Toto označenie derivácie zaviedol I. Newton). Teda nezávisle premennou v mnohých prípadoch vo fyzike je práve čas t. Pri výpočtoch zvážte, že v  matematike ste boli zvyknutí za nezávisle premennú považovať premennú x.

 

            Vektor v , určený rovnicou (2.1.10), udáva okamžitú rýchlosť pohybujúceho sa hmotného bodu v mieste A . Okamžitá rýchlosť v   je vektor, ktorý má smer dotyčnice ku dráhe v danom skúmanom okamihu a ktorý je určený jednotkovým vektorom  t  (pozri obr. 2.1.3) a môžeme ho napísať v tvare

 

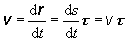                                                                                                  (2.1.11)

 

 t je jednotkový vektor v smere dotyčnice ku trajektórii skúmaného bodu, čiže | t | = 1 a je orientovaný na stranu pohybu. Ak dosadíme polohový vektor v zložkovom tvare, určený rovnicou  (2.1.1), do vzťahu (2.1.11),  pre okamžitú rýchlosť v   v sústave, v ktorej jednotkové vektory i, j, k sú konštantné čo do veľkosti i smeru, môžeme písať

 

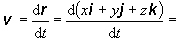
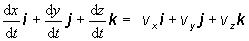                       (2.1.12)

 

Veličiny v_x, v_y a v_z nazývame zložkami rýchlosti spadajúcimi do smeru súradnicových osí.

Poznámka: Pri výpočte  sme použili pravidlá:

·      derivácia súčtu sa rovná súčtu derivácií jednotlivých sčítancov

·      derivácia súčinu konštanty s funkciou sa rovná súčinu konštanty s deriváciou funkcie.

 Za konštantu, ako sme už uviedli,  považujeme v tomto prípade i všetky tri jednotkové vektory i, j,k.  

Pre absolútnu veľkosť (hodnotu) vektora okamžitej rýchlosti platí vzťah

 

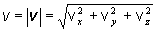.                                                                                          (2.1.13)                                                               

 

Pre uhly, ktoré zvierajú jednotlivé súradnicové osi s rýchlosťou v, (resp. pre  smerové kosínusy) platia vzťahy

 

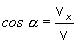
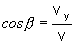
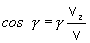                                                                     (2.1.14)

 

V sústave SI jednotkou rýchlosti je 1 m.s^-1.

                                                                                                                                                                                

·       Stredné zrýchlenie a okamžité zrýchlenie

            Nech v určitom časovom okamihu t₀ sa nachádza hmotný bod v mieste  A  určeným  polohovým vektorom  r₀  a má  okamžitú rýchlosť  v₀ . V čase t nech sa hmotný hod (častica) nachádza v bode B určenom  polohovým vektorom  r  a má  okamžitú rýchlosť v  . Za časový interval Dt  = t -t₀  zmenila sa veľkosť rýchlosti hmotného bodu o hodnotu Dv  = v - v_0. Zmena veľkosti  rýchlosti Dv  za jednotku času udáva stredné zrýchlenie a_s

 

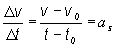                                                                                                                                                                        (2.1.15)           

Ak budeme zmenšovať časový interval Dt  až na nulu  t.j. Dt® 0, výraz

 

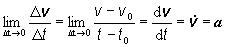                                                                          (2.1.16)

 

definuje okamžité zrýchlenie a. Je zrejmé, že  okamžité zrýchlenie sa rovná derivácii rýchlosti podľa času,  alebo druhej derivácii polohového vektora podľa času, ak za rýchlosť dosadíme vzťah určený rovnicou (2.1.11)

 

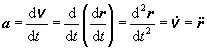                                                                              (2.1.17)

 

Analogicky ako  rýchlosť, tak i zrýchlenie môžeme rozložiť pomocou  pravouhlých zložiek

 

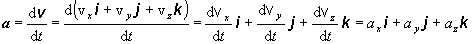                    (2.1.18)

 

(Pozn. Ak použijeme len pojem zrýchlenie,  máme na mysli okamžité zrýchlenie.)

 Pre veľkosť  okamžitého zrýchlenia a pre smerové kosínusy  platí

 

.                                                                                          (2.1.19)

 

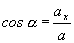
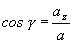                                                                          (2.1.20)

 

            Okamžité zrýchlenie udáva prírastok rýchlosti za jednotku času. Rozmer zrýchlenia v sústave SI je 1 m.s^-2.

            Vieme, že zrýchlenie je vektorová veličina a teda je určená nielen veľkosťou, ale i jej smerom. Smer zrýchlenie  vidíme z definície zrýchlenia, stanoveného rovnicou (2.1.16). Z nej vyplýva, že smer zrýchlenia je totožný so smerom vektora prírastku rýchlosti Dv.

____________________________

Príklad 2.1.2

Polohový vektor  pohybujúceho sa hmotného bodu závisí na čase podľa vzťahu  r(t) =A t³ i +Bt j +Ck, kde A = 1 m.s ^–3, B = 5 m.s^-1,C = -3 m. Určite :

 

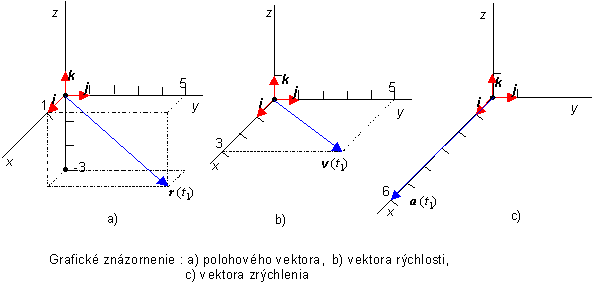
a)     vektory r, v, a v okamihu  t₁= 1 s a graficky  ich znázornite;

b)     veľkosti r, v, a v okamihu  t₁= 1 s ;

c)     smerové uhly r, v, a v okamihu  t₁= 1 s ;

d)     uhol  j, ktorý zvierajú vektor rýchlosti v a vektor zrýchlenia a v okamihu  t₂= 2 s ;

 

Riešenie:

 

a)     r(t) =A t³ i +Bt j +Ck = t³ i +5 t j -3 k,

 

 

      r(t₁) =  i +5 j -3 k, [m]                                                 

    

     

 

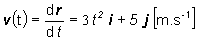
     v(t₁)  = 3 i + 5 j    [m.s^-1]                                                    

                                                  

                                                             

 

    

 

 

 

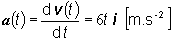
b)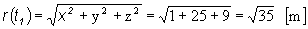    

 

 

     

 

 

     

 

 

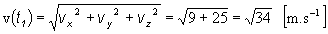
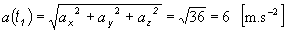
c)     smerové kosínusy a smerové uhly polohového vektora r (t₁):

 

 

 

 

 

 

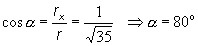
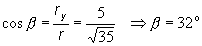
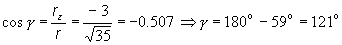
smerové kosínusy a smerové uhly vektora rýchlosti v(t₁):

 

 

 

 

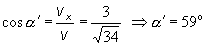
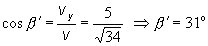
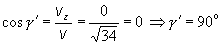
smerové kosínusy a smerové uhly vektora  zrýchlenia  a(t₁):

 

 

 

 

 

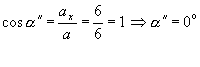
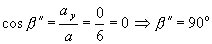
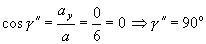
d)uhol vektorov rýchlosti a zrýchlenia v časovom okamihu  t₂ = 2 s

 

Určime vektor rýchlosti v danom okamihu: v(t₂) = 3.4 i + 5 j.  Určime vektor zrýchlenia v danom okamihu:  a(t₂) = 6 i .  Ich uhol možno vypočítať použitím skalárneho súčinu

 

 

 

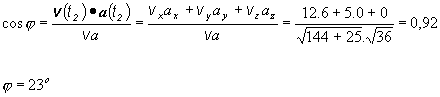
Príklad 2.1.3

Polohový vektor pohybujúcej sa častice je v SI sústave  určený vzťahom r(t)= (At²-Bt-C)i+(Dt+1)j,  kde A =2 m.s^-2, B = 3 m.s^-1, C = 2 m, D = 4 m.s^-1.Určite

a)     veľkosť vektorov r, v a a na začiatku pohybu, t.j. t₀ = 0 s,;

b)     graficky znázornite vektory r, v a a na začiatku pohybu;

c)     časový okamih t ₁, v ktorom vektor rýchlosti je rovnobežný s osou  y.

 

Riešenie: Keďže z-tová súradnica častice je nulová, častica sa pohybuje v rovine xy.

 

a)     r(t₀)= (2.0-3.0-2)i +(4.0+1) j = 2 i +j

 

 

 

 

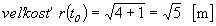
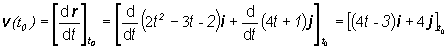
v(t₀)= -3 i +4 j   [m.s^-1]

 

veľkosť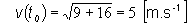

 

 

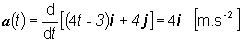
veľkosť      a (t₀) = 4  [m.s^-2]

 

 

 

b)

 

 

 

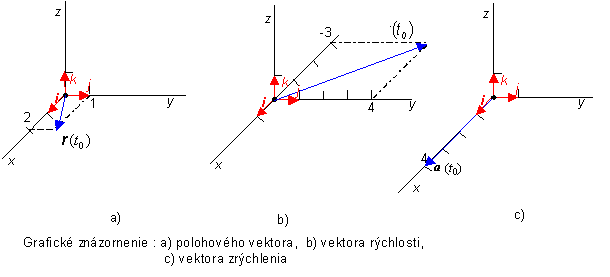
c ) Vektor rýchlosti je určený predpisom v(t)= (4 t –3)i + 4j.  Ak má byť vektor rovnobežný s osou y,  

    jeho x-ová zložka musí byť nulová, t.j. v_x (t₁)= 4 t₁  - 3 = 0  Þ t₁   = 3/4 s