2.1.5  Pohyb hmotného bodu v homogénnom tiažovom poli

V tejto časti nás bude zaujímať pohyb bodu v homogénnom tiažovom poli a to z hľadiska len kinematického. Z hľadiska dynamického sa mu budeme venovať neskôr. Skúmajme, ako sa bude pohybovať hmotný bod v homogénnom tiažovom poli, ktoré je charakterizované tým, že  v každom bode poľa tiažové zrýchlenie má konštantnú veľkosť i smer, t.j.

 

g= konšt.                                                                                                   (2.1.74)

 

Ak zanedbáme pôsobenie odporu prostredia ( napr. pri voľnom páde z malej výšky nad povrchom Zeme), bude sa zrýchlenie a, s ktorým sa pohybuje voľný hmotný bod v homogénnom tiažovom poli rovnať tiažovému zrýchleniu g. Na základe definície zrýchlenia dostaneme pre rýchlosť

 

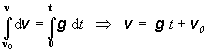                                                                       (2.1.75)

 

kde v₀   je počiatočná rýchlosť hmotného bodu v časovom okamihu t₀ =  0 . Polohový vektor hmotného bodu ako funkciu času dostaneme integráciou

 

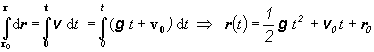                                    (2.1.76)

 

kde r₀  udáva polohový vektor hmotného bodu v časovom okamihu  t₀ =  0 , v ktorom mal rýchlosť v₀. Dráha pohybu leží v rovine určenej vektormi v₀ a g. To znamená, že pri  skúmaní pohybu v homogénnom tiažovom poli stačí pohyb skúmať  len ako rovinný pohyb,  ba dokonca v špeciálnom prípade (zvislý vrh nahor resp nadol ) ako pohyb po priamke. Dané rovnice závisia od voľby súradnicovej sústavy. Zvoľme si takú  súradnicovú sústavu xy, ktorej začiatok umiestnime na povrch Zeme, os y smeruje zvisle nahor a os x umiestnime tak, aby vektor v₀ ležal v rovine xy. Tiažové zrýchlenie vo zvolenej súradnicovej  sústave je

 

g = [0, - g, 0]                     resp.                      g  = - g j .                                      (2.1.77)

 

 

Počiatočná rýchlosť v₀

 

v₀ =  [v_0x, v_0y, 0]     resp.             v₀ = v_0x i + v_0y j .                                                (2.1.78)

 

 

Nech  v časovom okamihu t₀ = 0 , v ktorom začneme pohyb skúmať,  sa hmotný bod nachádzal v polohe určenom vektorom r₀

 

r₀ = [x₀, y₀, 0]       resp.             r₀ = x₀ i + y₀ j.                                                        (2.1.79)

 

Podľa počiatočných podmienok, určených r₀ a v_{0 ,} rozlišujeme nasledovné prípady pohybu hmotného bodu v homogénnom tiažovom poli:

·       Voľný pád - hmotný bod (teleso) je voľne spustené z výšky y₀  nad zemským povrchom.

·       Zvislý vrh nahor – hmotný bod je vrhnutý z povrch Zeme  zvisle nahor s počiatočnou rýchlosťou v_0, resp. z určitej výšky nad povrchom Zeme_.

·       Vodorovný vrh – hmotný bod je vo výške y₀ nad zemským povrchom vrhnuté v smere osi x počiatočnou rýchlosťou v_0.

·       Šikmý vrh - hmotný bod je vrhnutý šikmo z povrchu  Zeme  s počiatočnou rýchlosťou v₀  pod elevačným uhlom a  vzhľadom na os x.

Jednotlivé prípady pohybu hmotného bodu v homogénnom tiažovom poli získame riešením dvoch vektorových rovníc - (2.1.75) pre rýchlosť  a (2.1.76) pre polohu  hmotného s rôznymi počiatočnými podmienkami.

(Poznámka: Nasledovná časť, v ktorej rozoberieme jednotlivé prípady pohybu,  je  určená pre tých čitateľov, ktorí  nemali dobrý základ stredoškolskej fyziky, respektíve si  ho potrebujú zopakovať.)

 

 

Voľný pád

Ak počiatočné podmienky pri voľnom páde (obr. 2.1.14)  r₀ = [0, y₀, 0] ,  v₀ =  [0,0,0], dosadíme do vektorových rovníc (2.1.75) a  (2.1.76) s uvážením g = [0, - g, 0 ] , dostaneme skalárne rovnice pre vektor rýchlosti v = [0, - v_y, 0]  a polohový vektor r = [0, y, 0] v časovom okamihu  t

 

v_y =  g t                                                                                                                     (2.1.80)

 

                                                                                                        (2.1.81)

 

Dĺžka dráhy, ktorú  hmotný  bod  prejde  za  časový interval Dt  a   rýchlosť, ktorú  nadobudne  za  časový interval Dt,  možno vyjadriť vzťahmi

 

                                                                                                           (2.1.82)

                                                                                           

v =  Dt                                                                                                                   (2.1.83)      

                                                                                          

 

 

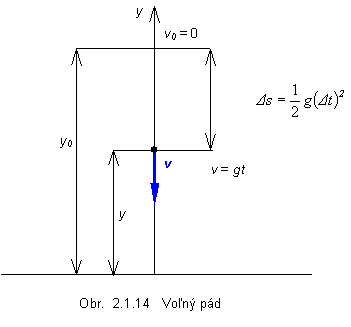
Časový okamih (čas dopadu)  t_D určíme z podmienky, že hmotný bod sa už nachádza na povrchu Zeme, t.j. y = 0 

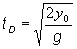                                                                                                                (2.1.84)

 

Rýchlosť telesa pri dopade na povrch Zeme v_D  určime z rovnice

                                                                                 (2.1.85)

_______________________________

 

Príklad 2.1.15

 Teleso padne z výšky 1 250 m voľným pádom. Určite a) za aký časový interval prejde prvý meter svojej dráhy, b) v ktorom čase t_D dopadne, c) dĺžku dráhy, ktorú  prejde počas štvrtej sekundy svojho pohybu, d) za aký časový interval prejde posledný meter svojej dráhy, e) o koľko mu vzrástla rýchlosť počas štvrtej sekundy pohybu.

Riešenie:

·        Vypíšeme zadané veličiny a veličiny, ktoré treba určiť:  y_v = 1250 m  a zrýchlenie telesa   a = g

·        Zvážime aký pohyb teleso koná a napíšeme počiatočné podmienky:  Teleso koná zvislý vrh nadol, ktorý predstavuje rovnomerne zrýchlený pohyb po priamke v smere zvolenej súradnicovej  sústavy. Počiatočné podmienky v₀ = [0, 0, 0], r₀ = [0, y₀, 0], g = [0,-g, 0]

·        Napíšeme základné  vektorové rovnice (2.1.75) a (2.1.76),  z ktorých vypočítame hľadané veličiny:

          

            

 

 

a) Prvý meter svojej dráhy prejde za časový interval Dt₁

 

 

 

b) Čas dopadu t_D určíme z rovnice

 

 

 

c) Dĺžku dráhy Ds, ktorú  prejde hmotný bod  počas štvrtej sekundy svojho pohybu určíme ako rozdiel polôh na konci tretej sekundy y₃  a na konci štvrtej sekundy y₄

 

 

d)  Časový interval Dt, za ktorý hmotný bod prejde  posledný meter svojej dráhy, určíme z rozdielu  Dt = t_D  - t_{1 ,} t.j. rozdielu  okamihu dopadu t_D a časového okamihu t_1,,  kedy hmotný bod  sa nachádza v polohe y₁ = 1 m nad povrchom.

 

 

e) Prírastok rýchlosť vo štvrtej sekunde Dv pohybu určíme ako rozdiel rýchlosti na konci štvrtej sekundy a rýchlosti na konci tretej sekundy.

 

_____________________________________

 

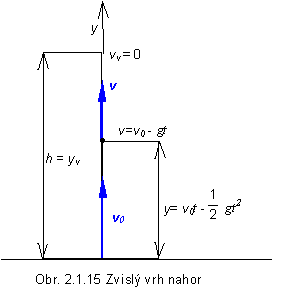
·       ­­­­­­­­­­­­­Zvislý vrh nahor

 

Zvislý vrh nahor možno realizovať ak telesu udelíme počiatočnú rýchlosť v smere osi y.  Skladá sa z pohybu, ktorý je  zložením priamočiareho rovnomerného pohybu s rýchlosťou v₀  vo zvislom smere nahor a voľného pádu (obr. 2.1.15). Počiatočné podmienky pri zvislom vrhu sú:             

 r₀ =  [0, 0, 0],    v₀  =  [0, v_0y, 0].

Po   ich  dosadení do rovníc  (2.1.75)  a  (2.1.76) a rozpísaní, dostaneme skalárne  rovnice  pre  rýchlosť v  = [0, - v_y, 0] a  polohový   vektor   r  =  [0, y, 0]

 

 

v_y = v₀ - t                                                                                                              (2.1.86)

                                                                                                       (2.1.87)

                                                                

Maximálnu výšku výstupu y_v, ktorú hmotný bod dosiahne za časový interval Dt = t_v –t₀ (obvykle  t₀ = 0 s) určíme z podmienky, že v danom časovom okamihu  t_v,           rýchlosť   hmotného   bodu v najvyššej  polohe je nulová a platí 

                   

 0 = v₀ - t_v                                                                                                              (2.1.88)

                                      

odkiaľ po úprave pre čas výstupu t_v dostaneme

                                                                                                                     (2.1.89) 

                            

Maximálnu výšku výstupu y_v určíme ak do rovnice (2.1.87) dosadíme čas výstupu podľa rovnice (2.1.89)    

            

                                                                                          (2.1.90)

 

Časový interval Dt_D = t_D –t_v , za  ktorý sa hmotný bod vráti  späť z maximálnej výšky y_v, na povrch Zeme t.j.  čas  dopadu t_D , určíme, ak si uvedomíme, že celková dĺžka dráhy, ktorú prejde hmotný bod je rovná maximálnej výške výstupu y_v, ktorú hmotný bod dosiahne. Hmotný bod padá voľným pádom, pretože jeho počiatočná rýchlosť je nulová. Z rovnice   (2.1.84 ) pre čas dopadu  t_D dostávame 

 

                                                                                                      (2.1.91)

 

Porovnaním rovníc (2.1.89) a  (2.1.91) vidíme, že čas výstupu t_v do maximálnej výšky je rovnaký ako čas pádu t_D  hmotného bodu z tejto výšky. Pre celkový časový interval D t_c , v ktorom teleso  koná pohyb pri zvislom vrhu nahor dostávame

 

                                                                                     (2.1.92)

 

Rýchlosť dopadu v_D určíme, ak do rovnice (2.1.86) dosadíme  celkový čas pohybu Dt_c

 

                                                                      (2.1.93)

 

Z rovnice  (2.1.93)  vidíme, že rýchlosť dopadu je čo do veľkosti rovnako veľká ako počiatočná rýchlosť v_D  , avšak má opačný smer, t.j.

 

v_D = - v₀                                                                                                                    (2.1.94)

 

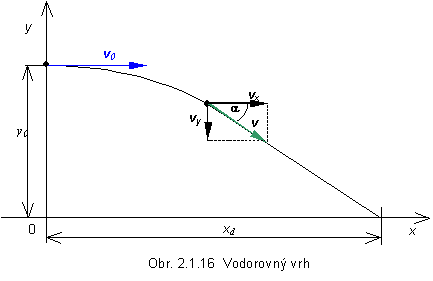
·       Vodorovný vrh

Vodorovný vrh možno realizovať, ak telesu nachádzajúcemu sa v určitej výške y₀ udelíme počiatočnú rýchlosť  v₀  v smere osi x (obr. 2.1.16).  Skladá sa z pohybu, ktorý je  zložením priamočiareho rovnomerného pohybu s rýchlosťou v₀ vo vodorovnom smere (os x) a z priamočiareho pohybu vo zvislom smere nadol ( voľný pád).

 

Počiatočné podmienky pri zvislom  vrhu  sú:  r₀ =  [0, y₀, 0], v₀ =  [v_0x, 0, 0]. Po  ich  dosadení  do  rovnice  (2.1.75)  a  rozpísaní, dostaneme pre  rýchlosť

 v = [v_x, v_y, 0] skalárne rovnice

 

v_x(t) = v₀                            v_y (t) = -g t    

 

resp. vo vektorovom tvare

 

v = v₀  i -g t j                                                                                                            (2.1.95)

 

Pre veľkosť rýchlosti  v platí rovnica

 

                                                                                                       (2.1.96)

 

Vektor rýchlosti hmotného bodu v ľubovolnom časovom okamihu má smer dotyčnice ku dráhe a možno ho určiť pomocou uhlu b, ktorý zviera s vodorovným smerom. Pre tento uhol platí

 

                                                                                                         (2.1.97)

Dosaďme počiatočné podmienky do rovnice (2.1.76) pre polohový vektor r(t)  a po jej  rozpísaní do zložiek, dostaneme rovnice pre súradnice  polohového vektora

r = [x, y, 0]

 

x = v₀ t                                                                                                                      (2.1.98)

  

                                                                                                          (2.1.99)

 

Časový okamih dopadu, t.j. čas dopadu t_D určíme z podmienky, že hmotný bod sa už nachádza na povrchu Zeme, t.j.

 

y = 0 

 

 

odkiaľ dostávame pre čas dopadu t_D  rovnaký vzťah ako pre čas dopadu pri voľnom páde

 

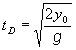                                                                                                               (2.1.100)

 

 

Rýchlosť dopadu v_D, t.j. rýchlosť, s ktorou teleso dopadne na povrch Zeme určíme, keď  do rovnice (2.1.96) dosadíme čas dopadu t_D

 

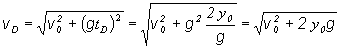                                             (2.1.101)

 

Miesto dopadu x_D určíme, ak do rovnice (2.3.60)  pre x-ovú súradnicu polohového vektora  dosadíme čas dopadu t_D

  

                                                                                              (2.1.102)

 

Rovnicu dráhy, po ktorej sa pohybuje hmotný bod pri vodorovnom vrhu získame, ak z parametrických rovníc dráhy (2.1.98) a (2.1.99) vylúčime parameter, ktorým je čas t :

 

                                                                                        (2.1.103)

  

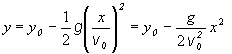                                                                        (2.1.104)

 

Rovnica (2.1.104) je rovnicou posunutej paraboly s vrcholom na osi y v bode V = [0, y₀]  a s osou spadajúcou do osi y.

 

 

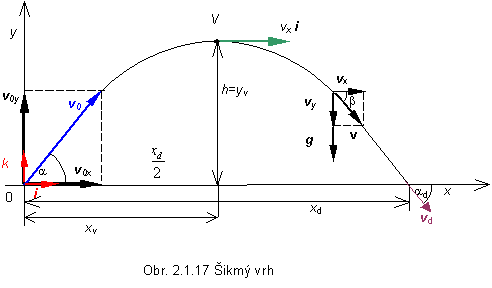
·       Šikmý vrh

 

Šikmý vrh koná teleso, ktorému bola na povrchu Zeme, resp. v určitej výške nad povrchom Zeme, udelená počiatočná rýchlosť v₀, ktorá zviera vzhľadom na vodorovnú rovinu (os x) elevačný uhol a (obr. 2.1.17). Počiatočné podmienky pri šikmom vrhu sú: r₀ =  [0, 0, 0],  v₀ =  [v_0x, v_0y, 0] = [v₀ cos a, v₀ sin a,0]. Po  ich  dosadení   do  rovnice (2.1.75)  a  rozpísaní, dostaneme  skalárne   rovnice  pre  rýchlosť

v = [v_x, v_y, 0]  

                                                                                    

v_x = v₀ cos a                                                                                                             (2.1.105)

 

v_y = v₀ sin a -g t                                                                                                       (2.1.106)

                                                                             

resp. vo vektorovom tvare   (v₀ cos a)i +( v₀ sin a -g t) j                                        (2.1.107)

                                                                 

Pre veľkosť rýchlosti  v platí rovnica

          

                                                                            (2.1.108)

 

Vektor rýchlosti hmotného bodu v ľubovolnom časovom okamihu má smer dotyčnice ku dráhe a možno ho určiť pomocou uhlu b, ktorý zviera s vodorovným smerom. Pre tento uhol platí opäť rovnaký vzťah (2.1.97) ako v prípade vodorovného vrhu, t.j.

 

                                                                                                      (2.1.97)

 

Dosaďme počiatočné podmienky pre rýchlosť

 

v_0x  = v₀  cos a                                                                                                            (2.1.109)

 

v_0y  = v₀  sin a                                                                                                            (2.1.110)

 

do vektorovej  rovnice  (2.1.76)  a po jej  rozpísaní, dostaneme rovnice pre súradnice  polohového vektora r = [x, y, 0]

 

x = v₀  t cos a                                                                                                            (2.1.111)

 

                                                                                              (2.1.112)

 

Vylúčením času t z parametrických rovníc dráhy (2.1.111) a (2.1.112) získame analytické vyjadrenie rovnice dráhy

 

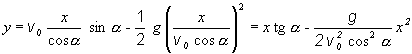                            (2.1.113)

 

Rovnica (2.1.113) predstavuje časť paraboly, s vertikálnou  osou (rovnobežnou  s osou y), ktorej začiatok je v bode V = [x_v, y_v] , kde x_v je miesto, v ktorom dosiahne hmotný bod maximálnu výšku y_v výstupu. Ak si uvedomíme, že šikmý vrh je pohyb zložený z rovnomerného priamočiareho pohybu v smere osi x s počiatočnou rýchlosťou v_{0x =} v₀ cosa, určenou rovnicou   (2.1.109) a zo zvislého vrhu s počiatočnou rýchlosťou v_y = v₀ sin a , postup výpočtu času výstupu t_{v, ,} času  pádu t_D, ako i ostatných charakteristických veličín pre tento pohyb je rovnaký.

 Čas výstupu t_v určíme z podmienky, že v najvyššej polohe rýchlosť má smer dotyčnice ku dráhe, t.j. vektor rýchlosti je rovnobežný s osou x a teda zložka rýchlosti  v_y = 0 

 

                                                                                                            (2.1.114)

 

 

Výšku výstupu y_v  určíme, ak do rovnice dráhy pre zvislý vrh (2.3.74) dosadíme čas výstupu t_v. Úpravou získame nasledovnú  rovnicu

 

                                                                                                          (2.1.115)

 

X-ovú súradnicu vrcholu paraboly x_v určíme, ak do rovnice pre dráhu v smere osi x dosadíme  čas výstupu t_v.

 

                                                                             (2.1.116)

 

Okamih dopadu (čas dopadu)  t_c určíme z podmienky, že hmotný bod sa už nachádza na povrchu Zeme, t.j. y = 0 

 

 

odkiaľ pre okamih dopadu  t_c dostávame

 

                                                                                                  (2.1.117)

 

Vidíme, že čas výstupu a čas zostupu  pri šikmom vrhu je rovnaký.

 

Miesto dopadu x_d určíme ak do rovnice pre x-ovú súradnicu polohy hmotného bodu (2.1.111)  dosadíme čas dopadu t_c

 

                                                           (2.1.118)

   

Rýchlosť dopadu v_D, s ktorou teleso dopadne na povrch Zeme určíme, ak do rovnice (2.1.108) dosadíme čas dopadu  t_c

                                         

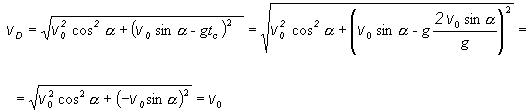(2.1.119)

 

 

Rýchlosť dopadu má rovnakú veľkosť ako počiatočná rýchlosť šikmého vrhu. Vektor rýchlosti dopadu určuje rovnica

 

                                                                          (2.1.120)

 

z ktorej určíme uhol dopadu a_D

 

 

Vidíme, že hmotný bod, ktorý sa pohybuje šikmým vrhom, dopadá na povrch  pod tým istým uhlom ako bol z povrchu vrhnutý.

 

Kontrolné otázky k časti 2.1.5

 

1.     Definujte homogénne tiažové pole.

2.     Kedy môžeme hovoriť o homogénnom poli Zeme?

3.     Z akých pohybov sa skladá šikmý vrh?

4.     Z akých pohybov sa skladá zvislý  vrh nahor?

5.     Napíšte matematické vyjadrenie veľkosti rýchlosti a dráhy voľne padajúceho telesa.

6.     O akom pohybe hovoríme, ak hmotný bod je vrhnutý z povrch Zeme  zvisle  nahor s počiatočnou rýchlosťou v_0.  Napíšte základné rovnice pre tento pohyb.

7.     Uveďte príklad vodorovného vrhu. Napíšte základné rovnice pre tento pohyb.

8.     Po akej trajektórii sa pohybuje častica, ktorej v určitej výške na povrchom Zeme bola udelená rýchlosť v smere rovnobežnom s povrchom Zeme?

9.     Je niektorá zložka vektora rýchlosti konštantná pri šikmom vrhu v homogénnom gravitačnom poli?

10.  Aká je rýchlosť telesa vrhnutého zvisle nahor v najvyššom bode jeho dráhy?

11.  Aký uhol zviera  vektor rýchlosti častice konajúcej šikmý vrh  v najvyššom bode jej dráhy  s osou nezávisle premennej, ktorou je čas t?

12.   Z akej podmienky vypočítame čas  výstupu častice pri zvislom vrhu nahor?

13.  Z akej podmienky vypočítame výšku  výstupu častice pri zvislom vrhu nahor?

14.  Z akej podmienky vypočítame miesto dopadu častice pri šikmom vrhu nahor?

15.  Pri akom elevačnom uhle dopadne častica pri šikmom vrhu do najvzdialenejšej polohy?

16.  S akou rýchlosťou dopadne na Zem častica, ktorá bola vrhnutá zvisle nahor? (Odpor vzduchu neuvažujeme.)

17.  Možno pre zvislý vrh nahor použiť rovnice pre šikmý vrh?  Ak áno, za akej podmienky?

18.  Možno pre vodorovný vrh  použiť rovnice pre šikmý vrh?  Ak áno, za akej podmienky?

19.  Možno použiť rovnice paraboly v parametrickom tvare pre opis šikmého vrhu?

20.  Napíšte parametrické rovnice pre rýchlosť i dráhu, opisujúce šikmý vrh.