B) Nerovnomerný priamočiary pohyb

            Ak sa pohybuje hmotný bod (teleso) s rýchlosťou, ktorá nie je konštantná, ale sa istým spôsobom s časom mení, hovoríme, že hmotný bod  koná nerovnomerný pohyb. Špeciálnym prípadom nerovnomerného pohybu je pohyb rovnomerne zrýchlený.

 

·     Rovnomerne zrýchlený priamočiary pohyb

 

            Rovnomerne zrýchlený pohyb je taký pohyb, pri ktorom fyzikálna veličina zrýchlenie  je konštantná t.j. 

 

 a  = konšt.                                                                                                                       (2.1.44)

 

Pre rovnomerne zrýchlený pohyb platí, že  zmena vektora rýchlosti Dv za  ľubovolné,  avšak rovnako veľké časové intervaly Dt, je konštantná. Ak  vektor zrýchlenia  je konštantný, čo do veľkosti i smeru, jedná sa o rovnomerne zrýchlený priamočiary pohyb.  Rovnice pre rýchlosť  získame riešením vektorovej rovnice (2.1.17)

 

 

ktorú prepíšeme do troch skalárnych rovníc pre jednotlivé súradnice vektora zrýchlenia  a = [a_x, a_y, a_z] a vektora rýchlosti v = [v_x , v_y , v_z] . Rovnice pohybu získame riešením troch  skalárnych rovníc  nasledovným postupom: 

 

 

 

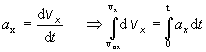
Po integrovaní a dosadení počiatočných podmienok v ₀ =[v_ox, v_oy , v_oz] ,  t_o =  0 , dostaneme pre x-ovú zložku rýchlosti 

 

v_x -v_ox =  a_x t    resp. v_x(t)  = v_ox + a_x t                                                                        (2.1.45)

 

Rovnakým spôsobom získame i časovú závislosť pre  y-ovú a z-ovú zložku rýchlosti rovnice

 

v_y -v_oy =  a_y t    resp.    v_y(t)  = v_oy + a_y t                                                                        (2.1.46)

 

v_z -v_oz =  a_z t     resp. v_z(t)  = v_oz+ a_z t                                                                            (2.1.47)

 

 

            Ak skúmame pohyb v rovine x,y  pravouhlej  súradnicovej sústavy,  pohybové rovnice  sú určené rovnicami (2.1.45) a (2.1.46).

            V prípade, ak sa hmotný bod pohybuje v kladom smere osi x  t.j. v  =  [v_x, 0, 0] a na počiatku mal rýchlosť v₀ =  [v_0x, 0, 0], matematický  vzťah,  určený  rovnicou  (2.1.45)  vyjadruje  časovú  závislosť rýchlosti   pohybu hmotného bodu pri rovnomerne zrýchlenom  priamočiarom pohybe. Ak by sme zvolili za počiatok skúmania pohybu okamih t_o ,  rovnica  (2.1.45)  prejde do tvaru

 

v_x-v_ox = a_x (t- t_o )              resp.                Dv_x = a_x Dt                                                       (2.1.48)

 

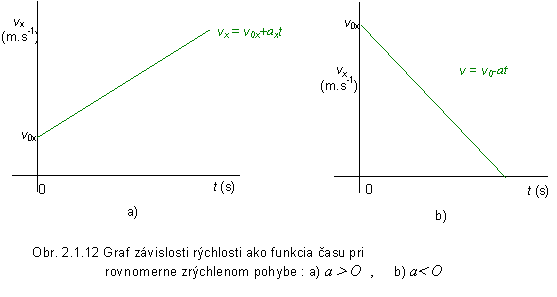
            Ak počiatočná rýchlosť v_ox je menšia ako konečná rýchlosť v_x,  t.j. v_x > v_o , zrýchlenie je kladná veličina ( a_x > O ), hovoríme o rovnomerne zrýchlenom pohybe. V prípade   v_x< v_o hovoríme o rovnomerne  spomalenom pohybe ( a_x< O ). Závislosť veľkosti rýchlosti  rovnomerne zrýchleného pohybu ako funkcia  času je priamka znázornená na obr. 2.1.12

 

 

Rovnice pre dráhu  hmotného bodu získame riešením vektorovej rovnice (2.1.10)

  

 

ktorú rozpíšeme do troch skalárnych rovníc

 

                                                                     

 

po dosadení časovej   závislosti jednotlivých  zložiek rýchlosti, danej rovnicami (2.1.45)  až (2.1.47). (Poloha hmotného bodu na začiatku skúmania pohybu je určená polohovým vektorom r₀ = [x_o, y_o , z_o] a  súradnice polohového vektora hmotného bodu v ľubovolnom časovom okamihu t sú r = [x, y, z]).

            Riešenie si  ukážeme na prípade, ak smer  pohybu  je  kladný  smer osi  x . Vtedy  r₀  = [x_o, 0, 0]  a  r  = [x, 0, 0], a v  = [v_x, 0, 0], v ₀  = [v_0x, 0, 0], a =[a_x, 0, 0]. Vektorová rovnica (2.1.10) v tomto prípade prejde na tvar .

 

 

Celková dráha, ktorú ubehne skúmaný hmotný bod za  časový interval t = t-t₀ bude

 

 

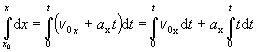
kde sme položili  t₀ = 0 s. Po integrovaní dostávame

 

 

 resp.

 

                                                                                                 (2.1.49)

 

Ak na začiatku pohybu sa hmotný bod nachádza v pokoji, t.j. v ₀ = 0  a v začiatku zvolenej súradnicovej sústavy, je závislosť dráhy od času ( v kladnom smere osi x ) pri rovnomerne zrýchlenom pohybe daná rovnicou

 

                                                                                                                

 

Grafické znázornenie  závislosti dĺžky dráhy od času pri rovnomerne zrýchlenom pohybe hmotného bodu je na  obrázku 2.1.13 a. Dĺžka dráhy, ktorú hmotný bod  prejde za časový interval < 0, t₁ > sa číselne rovná obsahu vyšrafovaného štvoruholníka na obr. 2.1.13 b . Z obrázkov vidieť, že rýchlosť pri priamočiarom rovnomernom pohybe je lineárnou funkciou času a dráha je kvadratickou funkciou času a  zrýchlenie je konštantné obr. 2.1.13 c.

 

·       Nerovnomerne zrýchlený priamočiary pohyb

 

            Vo všeobecnosti zrýchlenie sa môže s časom meniť podľa ľubovolnej funkcie t.j.

 

  a = a (t)                                                                                                                          (2.1.52)

 

V tomto prípade si musíme opäť uvedomiť, že pre daný pohyb platia len dve základné rovnice definujúce  zrýchlenie (2.1.17) a  rýchlosť (2.1.10):

 

                                   

 

Postup záleží od toho, ktorú veličinu máme zadanú a  ktorú chceme určiť. V prípade priamočiareho pohybu, ak začiatok súradnicovej sústavy leží na priamke, po ktorej sa hmotný bod pohybuje, možno prepísať každú z vektorových rovníc do jednej skalárnej rovnice. (Smer pohybu je určený  smerovým vektorom priamky. Najčastejšie orientujeme pohyb do kladnej osi x, kedy platí:  v = [v,0,0]   a = [a,0,0] r = [x,0,0]   )

·     Ak chceme určiť závislosť rýchlosti od času, získame  ju nasledovným spôsobom:

1)  Dosadíme do  rovnice pre zrýchlenie  (2.1.17) za zrýchlenie konkrétnu funkciu určenú vzťahom  a = a_(t) .

2)  Následne vykonáme matematické úkony.

 

 

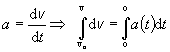
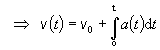                                                      (2.1.50)  

 

Týmto  získame  pre zadaný konkrétny  prípad časovej závislosti zrýchlenia  a = a(t),  konkrétnu funkčnú závislosť   v = v(t).

·     Ak chceme určiť závislosť dráhy  od času pre nerovnomerný priamočiary  pohyb, získame ju nasledovným spôsobom:

1)  Dosadíme do  rovnice pre rýchlosť (2.1.10) vzťah  (2.1.50).

2)  Vykonáme naznačené úkony

 

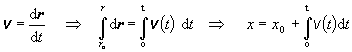                                                                              (2.1.51)

 

Konečnú hodnotu rýchlosti a ubehnutú dráhu za určitý časový interval získame po dosadení numerických hodnôt do vzťahov určených rovnicami  (2.1.50) a  (2.1.51). Naznačený postup si ozrejmíme na príkladoch 2.1.4 – 2.1.8.

 

Kontrolné otázky k časti 2.1.2

 

1.     Z hľadiska akých dvoch fyzikálnych veličín možno klasifikovať  pohyb? Definujte tieto veličiny a urobte klasifikáciu pohybov.

2.     Teleso sa pohybuje s normálovým zrýchlením rovným nule. Aká môže byť jeho  dráha v tomto prípade?

3.     Vyjadrite časovú závislosť dráhy pre pohyb priamočiary  rovnomerne zrýchlený so zrýchlením a,  ktorého začiatočná rýchlosť bola nenulová. Zvážte možné prípady.

4.     Nakreslite grafickú závislosť rýchlosti hmotného bodu ako funkciu času, ak sa hmotný bod  pohybuje priamočiaro v smere osi x : a) rovnomerne , b) rovnomerne zrýchlene.

5.     Nakreslite grafickú závislosť  zrýchlenia hmotného bodu ako funkciu času, ak sa hmotný bod  pohybuje priamočiaro v smere osi y : a) rovnomerne , b) rovnomerne zrýchlene.

6.     Nakreslite grafickú závislosť polohy hmotného bodu ako funkciu času, ak sa hmotný bod  pohybuje priamočiaro v smere osi x : a) rovnomerne , b) rovnomerne zrýchlene.

7.     Aký pohyb koná hmotný bod , ak celkové zrýchlenie sa rovná tangenciálnemu zrýchleniu? Zložka  tangenciálneho zrýchlenia klesá s druhou mocninou času.

8.     Teleso sa pohybuje s konštantným celkovým zrýchlením. V tomto prípade jeho dráha musí mať tvar priamky?

9.     Napíšte rovnicu trajektórie častice, ktorú spustíme v gravitačnom poli Zeme a) s nulovou počiatočnou rýchlosťou, b) s nenulovou počiatočnou rýchlosťou z výšky y₀ nad Zemou.

10.  Čo je grafom závislosti dráhy od času pri rovnomernom priamočiarom pohybe?

11.  Aký pohyb koná teleso vrhnuté zvisle nahor   s nenulovou počiatočnou rýchlosťou?

12.  Aký pohyb koná častica, ktorá v ľubovolných, ale rovnakých časových intervaloch, prejde rovnaké dráhy?

13.  Grafom závislosti veľkosti rýchlosti od času pri rovnomerne zrýchlenom pohybe je priamka rovnobežná s osou, na ktorú nanášame nezávisle premennú veličinu, ktorou je čas. Aký pohyb zodpovedá danému grafu?