2.1.4 Pohyb po kružnici

 

            Každý krivočiary pohyb možno v infinitezimálne malom časovom intervale Dt  považovať  za pohyb po kružnici. Z tohto dôvodu   venujeme pohybu po kružnici špeciálnu  pozornosť napriek tomu, že sme si všeobecne platný  základ už postupne  ozrejmili v predchádzajúcich častiach.

            Pohyb po kružnici je najjednoduchším krivočiarym pohybom, pre ktorý platí:

·     trajektória pohybu je rovinnou krivkou;

·     rovina, v ktorej sa uskutočňuje pohyb je súčasne oskulačnou rovinou;

·     polomer krivosti je vo všetkých  bodoch dráhy rovnaký a rovná sa polomeru kružnice R;

·     stred krivosti trajektórie hmotného bodu má konštantnú polohu v strede kružnice S;

·     pohyb je charakterizovaný uhlovou dráhou  j =j (t);

·     vzťah medzi dráhou s  a uhlovou dráhou j   je:  s = j R;

·     rýchlosť hmotného bodu je určená obvodovou rýchlosťou v;

·     rýchlosť otáčania spojnice stredu kružnice s hmotným bodom  popisuje uhlová rýchlosť w ,  definovaná ako časová derivácia uhlovej dráhy,  t.j. w  = dj/dt

·     súvislosť medzi obvodovou a uhlovou rýchlosťou udáva vzťah v  =  w  x R ;

·     veličina, ktorá súvisí so zmenou veľkosti obvodovej rýchlosti v hmotného bodu po kružnici je  uhlové  zrýchlenie  a,  definované  ako  časová  derivácia uhlovej  rýchlosti,  t.j. a = dw /dt

·     celkové zrýchlenie hmotného bodu, možno rozložiť na tangenciálnu a normálovú zložku, pre ktoré platí 

     a = a_t + a_n =( a ´ r )+ (w ´ v) , kde a  je uhlové zrýchlenie, w  je uhlová rýchlosť, r je polohový vektor hmotného bodu   a v  obvodová rýchlosť, s ktorou sa hmotný bod pohybuje;

·     tangenciálna zložka zrýchlenia určuje nerovnomernosť pohybu a je určená  a_t =  a  Rt

·     normálová zložka zrýchlenia spôsobuje  zmenu smeru a je určená vzťahom:

            ,

 

    ktoré tiež nazývame dostredivé zrýchlenie. (r je jednotkový vektor so začiatkom v strede   kružnice S. )

·     veľkosť celkového  zrýchlenia hmotného bodu je určená vzťahom

 

         

 

________________________________

Príklad 2.1.12

Odvoďte vzťah udávajúci súvislosť medzi vektorovými veličinami obvodovou  rýchlosťou v, uhlovou rýchlosťou w a polohovým vektorom hmotného bodu pohybujúceho sa po kružnici o polomere R.

Riešenie: Súvislosť medzi vektorovými veličinami obvodovou  rýchlosťou v, uhlovou rýchlosťou w a polohovým vektorom hmotného bodu pohybujúcim  sa po kružnici o polomere R udáva vektorová rovnica  v = w x R, , ktorú odvodíme nasledovným postupom: Štúdiom obr. 2.1.6 v časti 2.1.1 sme dospeli k vzťahu pre uhol  dj,  ktorý opíše sprievodič za infinitezimálne malý časový interval dt pri pohybe  po kružnici s polomerom R, pri ktorom hmotný bod  opíše oblúk dĺžky ds

 

  

 

Derivovaním tejto rovnice  podľa času dostaneme

 

      

 

vzťah medzi veľkosťou obvodovej  a  veľkosťou uhlovej rýchlosti

 

v = R w                                                                                                                                  (a)

 

Rovnicu (a)  možno zapísať do vektorového tvaru, ak si uvedomíme smery jednotlivých vektorov vo všeobecnom prípade. Polohový vektor hmotného bodu pohybujúceho sa rovnomerným pohybom po kružnici  o polomere R, je určený vektorom R = Rr,   kde r  je jednotkový vektor v smere polohového vektora. Obvodová rýchlosť v = vt, kde t je jednotkový vektor v smere okamžitej rýchlosti (smer dotyčnice ku dráhe). Uhlová rýchlosť otáčania polohového vektora je w = w n . Pohyb po kružnici sa uskutočňuje v rovine, takže jednotkové vektory r, t, n sú navzájom kolmé. Z vlastností vektorového súčinu vyplýva, že ich možno zapísať   

 

                                                                                                                             (b)

 

Ak  rovnicu (a) a  (b)  dosadíme do vzťahu pre okamžitú rýchlosť, (vzťah 2.1.11)  dostaneme hľadaný vzťah

 

 

 

·     Rovnomerný pohyb po kružnici

            Pri rovnomernom pohybe po kružnici je  uhlové zrýchlenie  a  nulové,  veľkosť obvodovej rýchlosti sa nemení  ( v = konšt.)  a  uhlová rýchlosť ostáva tiež konštantná, teda

 

 w = konšt.   0

 

Závislosť uhlovej dráhy od času získame integráciou uhlovej rýchlosti:

 

                                                                                  (2.1.54)

 

kde integračná konštanta  j₀ je uhol, ktorý zviera polohový vektor pohybujúceho sa  bodu vzhľadom na stred kružnice v čase t = 0 s určitým, za základ zvoleným smerom polohového vektora. Obvykle volíme j₀ = 0 , v tomto prípade pre uhlovú dráhu pri rovnomernom pohybe po kružnici dostaneme

 

j = w t                                                                                                                      (2.1.55)

 

Rovnomerný pohyb po kružnici je pohyb periodický s  periódou T .Časový interval, za ktorý hmotný bod obehne raz po kružnici, t.j. dráhu 2p R  resp. uhlovú dráhu

a = 2p ,  sa nemení a nazývame ho  perióda T.

 

                                                                                                                                                                (2.1.56)

 

Prevrátená hodnota periódy sa nazýva frekvencia  f. Frekvenciou f označujeme počet obehov za jednotku času. Jednotkou frekvencie je s^-1 a nazýva sa Hertz (Hz).

 

                                                                                                                        (2.1.57)

 

Pre uhlovú rýchlosť w  potom píšeme

 

w = 2p f                                                                                                                    (2.1.58)

 

Ak hmotný bod za určitý časový interval  Dt vykoná n otáčok,  potom platí

 

                                                                                                                      (2.1.59)

 

Dráhu, ktorú opíše hmotný bod pohybujúci sa rovnomerným pohybom po kružnici s polomerom R a s frekvenciou f, ak vykonal n otáčok za časový interval  Dt, určíme:

 

Ds = vDt = w R Dt = 2 p f RDt                                                                                  (2.1.60)

 

Pre veľkosť obvodovej rýchlosti  dostaneme

 

                                                                                                 (2.1.61)

 

Vektor celkového zrýchlenia a pri rovnomernom  pohybe po kružnici je nenulový vektor, s veľkosťou v²/R a so  smerom do stredu kružnice (binormály, t.j. normály  na dotyčnicu k dráhe). Hovoríme tiež o dostredivom zrýchlení.

 

                                                                                                        (2.1.62)

 

Odvodenie  vzťahu (2.1.62) pre celkové zrýchlenie pri rovnomernom pohybe po kružnici si ukážeme v nasledujúcom príklade.

____________________________________

Príklad 2.1.13

 Graficky znázornite všetky veličiny, charakterizujúce rovnomerný pohyb po kružnici a určite s akým zrýchlením sa pohybuje hmotný bod pri tomto pohybe. Svoj grafický náčrt potvrďte  matematicky.

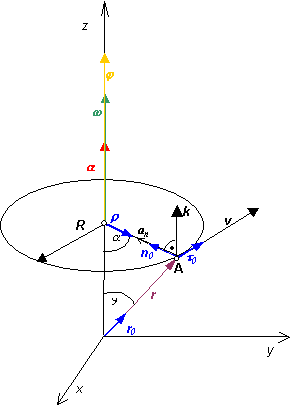
Riešenie: Zvoľme si pohyb po kružnici polomeru R do súradnicovej sústavy tak, že os otáčania splýva s osou z a stred kružnice S sa nachádza na osi z. Trajektória pohybu je teda  umiestnená do roviny x y. Hmotný bod sa pohybuje v smere proti pohybu hodinových ručičiek. Polohový vektor r hmotného bodu A má konštantnú veľkosť a zviera s osou z konštantný uhol J. V každom časovom okamihu pohybu platí R = r sinJ. V okamihu, v ktorom ideme rozhodnúť o smeroch jednotlivých vektorov, poloha hmotného bodu A  je  určená polohovým vektorom r = r r₀

 

 

 

Z definície vektora  uhlovej rýchlosti w  vieme, že vektor uhlovej rýchlosti je  vektor kolmý na rovinu, v ktorej sa pohyb odohráva a smeruje do tej polroviny, z ktorej vidím otáčanie polohového vektora r proti smeru hodinových ručičiek. V nami zvolenom prípade možno teda vektor uhlovej rýchlosti w  vyjadriť

 

w = w k

 

Určime smer vektora obvodovej rýchlosti v okamihu,  keď hmotný bod je v polohe rovnobežnej s osou y (t.j. jednotkové vektory j  a r sú súhlasne rovnobežné ). V tomto okamihu platí

 

 v =w   r = w k x r r₀  = w  r ( k  r₀) =w r ( k  r₀)  = w r sinJ (-i) =w R sinJ (-i)  = - vi

 

Ukázali sme, že rýchlosť v , v nami zvolenom okamihu má smer zápornej osi x osi, t.j. smer dotyčnice ku dráhe. Musíme si uvedomiť, že smer vektora obvodovej rýchlosti sa s časom neustále mení. V ľubovolnom časovom okamihu smer vektora obvodovej rýchlosti je určený vždy smerom dotyčnice ku dráhe pohybu, t.j. jednotkovým vektorom t₀, ktorý je kolmý  na vektor w , tak i na vektor R. Všeobecne potom z vlastností vektorového súčinu môžeme písať

 

v  =  w ´ r

 

Pre zrýchlenie potom dostaneme

 

                                                               

 

Člen v prvej zátvorke  je kolmý na a a r, má smer dotyčnice ku trajektórii pohybu., určuje tangenciálne zložku zrýchlenia. Člen v druhej zátvorke je kolmý na w  i v súčasne, má smer hlavnej normály, určuje normálovú zložku. Zrýchlenie bodu pohybujúceho sa po kružnici je určené vzťahom (2.1.21)   

 

 

kde tangenciálna zložka je

 

a_t =a x r  Þ  a_t = a r sin J. = a R

 

Pre normálovú zložku zrýchlenia, t.j. pre dostredivé zrýchlenie dostaneme vo vektorovom tvare

 

a_n =w  x v       Þ    a_n = w  v sin 90⁰  = w  v =  w ² R           

 

Tangenciálne zrýchlenie  je nulové, pretože derivácia konštanty (veľkosti obvodovej rýchlosti) je rovná nule, resp. a = 0. Celkové zrýchlenie hmotného bodu pohybujúceho sa čo do veľkosti  konštantnou rýchlosťou v po kružnici, je určené len normálovou zložkou zrýchlenia. Normálová zložka zrýchlenia a_n smeruje do stredu krivosti a je rôzna od nuly. 

 

 

 .

 

Týmto spôsobom sme opäť dospeli  k zhodnému vzťahu  pre normálovú zložku zrýchlenia danú vzťahom (2.1.23).

 

 

·     Rovnomerne zrýchlený  pohyb po kružnici

           

            Špeciálnym prípadom nerovnomerného pohybu po kružnici je rovnomerne zrýchlený pohyb. Je charakterizovaný tým, že uhlové zrýchlenie  w  je konštantné. Uhlovú  rýchlosť, ktorú hmotný bod má v čase  t určíme zo vzťahu (2.1.31)

 

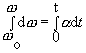                                                                                                            (2.1.63)

 

Po zintegrovaní  pre veľkosť uhlovej rýchlosti dostaneme

 

                                                                                                      (2.1.64)

 

a pre smer vektora uhlovej rýchlosti

w  =w  k                                                                                                                   (2.1.65)

 

Celkovú uhlovú dráhu určíme  zo vzťahu (2.1.30), do ktorého dosadíme rovnicu  (2.1.64) , určujúcu časovú závislosť uhlovej rýchlosti

 

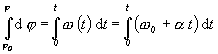                                                                           (2.1.66)

  

Po integrácii  rovnice  (2.1.66) pre uhlovú dráhu dostávame

 

                                                                                              (2.1.67)

 

j₀ je uhol, ktorý zviera polohový vektor pohybujúceho sa  bodu vzhľadom na stred kružnice v čase t = 0 s určitým, za základ zvoleným smerom polohového vektora. Obvykle volíme j₀ = 0,  w ₀ je  uhlová rýchlosť v čase t = 0 a a  konštantné zrýchlenie. Keďže v každom okamihu v = w  R    a   s =R j    môžeme písať

 

                                                                                                        (2.1.68)

 

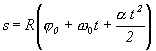                                                                                           (2.1.69)

V prípade, že a >  0 hovoríme o pohybe rovnomerne zrýchlenom,  orientácia vektorov w a a je súhlasná . Ak a < 0 hovoríme o pohybe rovnomerne spomalenom, orientácia vektorov w  a a je nesúhlasná. V tomto prípade však  uhlová rýchlosť w ₀ v čase t =0  musí byť rôzna od nuly  a postupne sa  s časom zmenšuje až na nulovú hodnotu.  Pre tangenciálnu zložku zrýchlenia pri rovnomerne zrýchlenom pohybe platí

 

                                                                                (2.1.70)

 

resp. vo vektorovom tvare

 

                                                                                                               (2.1.71)

 

Pre  normálovú zložku zrýchlenia pri rovnomerne zrýchlenom pohybe platí

 

                                                                                 (2.1.72)

 

resp. vo vektorovom tvare

 

                                                                                                                (2.1.73)

 

______________________________________

Príklad 2.1.14

Hmotný bod sa začal pohybovať po kružnici polomeru r  s konštantným uhlovým zrýchlením a . V ktorom časovom okamihu bude vektor zrýchlenia zvierať uhol b = 60 ⁰ s vektorom rýchlosti v?

 

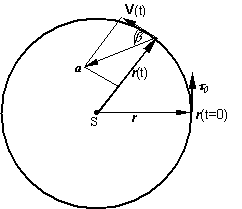
Riešenie: Kým začneme riešiť je vhodné si uvedomiť skutočnosti:

·      Jedná sa o rovnomerne zrýchlený pohyb po kružnici so začiatočnými podmienkami j₀ = 0 a w ₀ = 0.

·      Vektor rýchlosti v má smer dotyčnice ku trajektórii pohybu.

·      Vektor zrýchlenia rozložíme na tangenciálnu a normálovú zložku.

·      Vektor rýchlosti  je kolineárny (rovnobežný) s tangenciálnou zložkou zrýchlenia.

·      Uhol b, ktorý zviera vektor zrýchlenia s vektorom rýchlosti je aj uhol, ktorý zviera vektor zrýchlenia s vektorom tangenciálnej zložky zrýchlenie, pre ktorý platí:

 

 

 

 

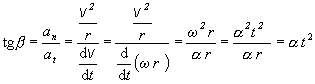
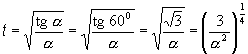
 Kontrolné otázky k časti 2.1.4

 

1.     Charakterizujte otáčavý pohyb.

2.     Definujte a) rovnomerný, b) nerovnomerný pohyb po kružnici.

3.     Vysvetlite   fyzikálny význam   uhlovej rýchlosti w.

4.     Ak sa častica pohybuje rovnomerným pohybom po kružnici, je nenulové jej zrýchlenie?

5.     Napíšte a definujte, ktoré veličiny charakterizujú pohyb po kružnici.

6.     Napíšte jednotku uhlovej rýchlosti a uhlového zrýchlenia.

7.     Pod vplyvom pôsobenia akej fyzikálnej veličiny sa mení priamočiary pohyb na pohyb po kružnici?

8.     Napíšte vzťah pre obvodovú rýchlosť častice pohybujúcej sa rovnomerným pohybom po kružnici s polomerom r a s uhlovou rýchlosťou w.

9.     Napíšte súvis periódy  T s frekvenciou  f  pri rovnomernom pohybe po kružnici.

10. Napíšte súvis medzi periódou   T a uhlovou rýchlosťou pri rovnomernom pohybe po

      kružnici.

11.  S akou uhlovou rýchlosťou sa pohybuje a) sekundová, b) minútová, c) hodinová ručička

      na hodinách?

12.  Je vektor rýchlosti konštantný pri rovnomernom pohybe po kružnici?

13.  Je vektor zrýchlenia konštantný pri rovnomernom pohybe po kružnici?

14.  Definujte vektor uhlového zrýchlenia a napíšte jeho jednotku.

15.  Napíšte jednotku uhlovej rýchlosti v sústave SI.

16.  Akú  vzájomnú orientáciu majú vektory uhlovej rýchlosti, polohového vektora častice a  jeho obvodovej rýchlosti pri pohybe častice po kružnici?

17.  Napíšte matematické vyjadrenie pre dostredivé zrýchlenie pri pohybe po kružnici.

18.  Určite smer dostredivé zrýchlenie pri pohybe po kružnici.

19.  Napíšte matematické vyjadrenie pre tangenciálne  zrýchlenie pri pohybe po kružnici.

20.  Napíšte vzťah pre celkové zrýchlenie pri pohybe po kružnici.

21.  Určite ako sa zmení obvodová rýchlosť častice pohybujúcej sa konštantnou uhlovou rýchlosťou po kružnici, ak jej vzdialenosť od osi rotácie zmenšíme na polovicu?