2

2.1.2 Priamočiary pohyb

Pohyb bodu sa nazýva priamočiary, ak sa pri ňom nemení smer rýchlosti, a rovnomerný, ak sa pri ňom nemení absolútna hodnota rýchlosti. Ak sa nemení zrýchlenie, pohyb nazývame priamočiary rovnomerne zrýchlený.

Priamočiary pohyb je charakterizovaný tým, že :

· trajektória, ktorú opisuje hmotný bod je priamka;

· smer pohybu sa nemení a je určený smerovým vektorom priamky , napr. t, pre ktorý platí |t| = 1;

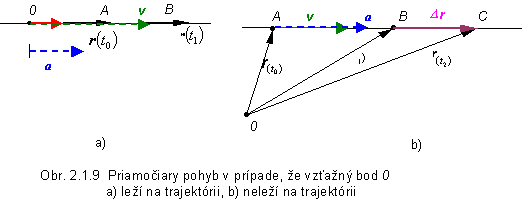
· vektor rýchlosti v a vektor zrýchlenia a sú súhlasne kolineárne, t.j. majú totožný smer, určený smerovým vektorom priamky t, po ktorej sa pohybuje bod v prípade, ak platí v (t₂) > v (t₁) (obr. 2.1.9 a), alebo nesúhlasne kolineárne v prípade v (t₂) < v (t₁) ;

· smer vektora rýchlosti v a vektora zrýchlenia a sa s časom t nemení;

· v prípade, že sme zvolili začiatok vzťažného systému O na priamke, ktorú opisuje hmotný bod, leží i polohový vektor r bodu A na tejto priamke a je kolineárny s vektorom rýchlosti i vektorom zrýchlenia (obr. 2.1.9 a).

A) Rovnomerný priamočiary pohyb

Hmotný bod koná rovnomerný priamočiary pohyb, ak za ľubovolné, avšak rovnako veľké časové intervaly Dt, prejde po priamke rovnakú dĺžku dráhy Ds. Z tejto definície vyplýva, že rýchlosť skúmaného objektu musí byť pri rovnomernom pohybe po priamke konštantná, čo do veľkosti i smeru. Smer pohybu nech je určený jednotkovým vektorom t. Potom platí

v = v t = konšt. (2.1.34)

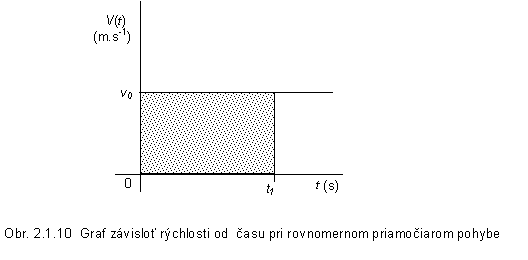
Grafickým znázornením závislosti veľkosti rýchlosti v = v(t) od času pri rovnomernom pohybe pri vyššie uvedených počiatočných podmienkach je vždy priamka, rovnobežná s časovou osou t ( obr. 2.1.10). Smernica tejto priamky, resp. tg a, sa rovná nule, nakoľko a = 0 resp. 180 ⁰ (a je uhol, ktorý priamka zviera s osou nezávisle premennej) .

Poznámka: Keďže smer vektora rýchlosti v pri priamočiarom pohybe sa nemení a je v každom časovom okamihu pohybu určený smerovým vektorom priamky t, vektorovú rovnicu (2.1.34) pri priamočiarom pohybe často nepíšeme, pretože sa zaujímame hlavne o veľkosť rýchlosti., resp. o dĺžku prebehnutej dráhy. Pri priamočiarom pohybe v týchto prípadoch stačí uvažovať skalárnu rovnicu t.j. v = konšt.

Rovnica v = konšt. (2.1.34) je ekvivalentná s rovnicou pre zrýchlenie

a = 0 (2.1.35)

pretože zmena rýchlosti, ani čo do veľkosti ani smeru, pri priamočiarom rovnomernom pohybe nenastáva. Zrýchlenie pri priamočiarom rovnomernom pohybe je nulové. Túto skutočnosť možno ukázať nasledovne: Pretože rýchlosť je konštantná t.j. v = v₀= konšt., smer pohybu sa nemení, pre zrýchlenie, definované vektorovou rovnicou (2.1.17) platí

nakoľko derivácia rýchlosti, t.j. derivácia konštanty je nula a pre zrýchlenie rovnomerného priamočiareho pohybu platí rovnica (2.1.35) t.j. a = 0, resp. a = 0.

Odvoďme matematické vyjadrenie časovej závislosti veľkosti dráhy pri rovnomernom priamočiarom pohybe. Túto rovnicu možno získať z definície rýchlosti (2.1.9) nasledovným spôsobom:

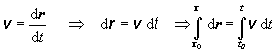
Hranice integrálu určujú, že hmotný bod na začiatku pohybu t.j. v okamihu t₀ sa nachádzal v mieste s polohovým vektorom r₀ a v okamihu t v mieste s polohovým vektorom r . Zložitosť výpočtu vektorovej rovnice závisí od voľby súradnicovej sústavy a bodu, vzhľadom na ktorý pohyb vzťahujeme. Ukážeme si to na dvoch rôznych prípadoch:

Prípad I.

Zvoľme nasledovný jednorozmerný súradnicový systém [O, t ], v ktorom:

· bod O znamená vzťažný bod, vzhľadom na ktorý pohyb skúmame ;

· bod O leží na trajektórii pohybu (obr. 2.1.9) ;

· smer pohybu je určený jednotkovým vektorom t, ktorý sa počas pohybu nemení.

Za týchto podmienok :

· vektor t je súčasne i smerovým vektorom priamky, po ktorej sa častica pohybuje;

· označme polohový vektory častice v okamihu t_o na začiatku skúmania pohybu r₀ a vyjadrime ho pomocou smerového vektora priamky, po ktorej sa hmotný bod pohybuje v tvare r₀ = s₀ t ;

· polohový vektory častice v ľubovolnom okamihu tskúmania pohybu označme r a vyjadrime ho pomocou smerového vektora priamky, po ktorej sa hmotný bod

pohybuje v tvare r = st;

· v okamihu t_o, keď začíname skúmať pohyb častice, nech sa častica nachádza vo vzdialenosti s₀od zvoleného začiatku súradnicovej sústavy O ;

· v ľubovolne zvolenom okamihu t sa častica nachádza vo vzdialenosti sod zvoleného začiatku súradnicovej sústavy O.

Keďže skúmame priamočiary rovnomerný pohyb v smere určenom jednotkovým vektorom t, ktorý sa nemení, bude nás zaujímať dĺžka prebehnutej dráhy Ds za časový interval Dt . Pri hore zvolených počiatočných podmienkach možno dĺžku dráhy Ds , ktorú častica za časový interval Dt = t – t_o prebehne, určiť po prepise vektorovej rovnice

dr = v dt na skalárny tvar

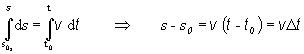
s = s_o + v (t-t_o) (2.1.36)

resp. na tvar

Ds = vDt (2.1.37)

Táto rovnica hovorí, že dĺžka dráhy, ktorú prejde hmotný bod, pohybujúci sa priamočiaro konštantnou rýchlosťou s veľkosťou v za časový interval Dt je číselne rovná ploche vyšrafovaného obdĺžnika na obr. 2.1.10.

V prípade, keď časticu v okamihu na začiatku skúmania pohybu, t.j. t_o= 0 , umiestnime do začiatku súradnicového systému [O, t], polohový vektor r₀=[0,0] a teda i jeho vzdialenosť s₀ od začiatku O sa rovná nule. Rovnica (2.1.37) v tomto prípade prejde na tvar

Ds= s = v t (2.1.38)

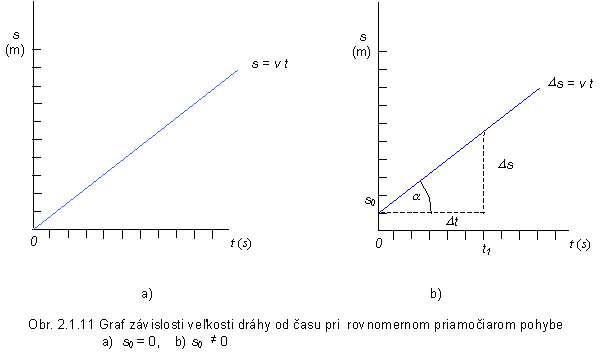
Rovnica (2.1.38) určuje závislosť dĺžky dráhy hmotného bodu ako funkciu času pri

rovnomernom priamočiarom pohybe. Grafickým znázornením závislosti dĺžky dráhy Ds= s = f( t) od času pri rovnomernom pohybe je vždy priamka, ( obr. 2.1.11). Smernica tejto priamky

-----------------------------------------

(Pozn.: V integráli ds znamená infinitezimálnu (elementárnu) dĺžku a pri integrovaní sme využili poznatok, že rýchlosť pri priamočiarom rovnomernom pohybe je konštantná a mohli sme ju vyňať pred integrál.)

resp. tg a udáva veľkosť rýchlosti. V prípade, že veľkosť jednotky dráhy a času je rovnaká, a je uhol, ktorý zviera priamka, po ktorej sa hmotný bod pohybuje, s osou nezávisle premennej, ktorou je čas t.

Prípad II.

Uvažujme pohyb hmotného bodu A po priamke, ak vzťažný bod O, vzhľadom na ktorý pohyb skúmame, neleží na trajektórii pohybu (obr. 2.1.9 b). V trojrozmernom priestore zvoľme karteziánsku súradnicovú sústavu, do začiatku ktorej umiestnime vzťažný bod O. Pohyb hmotného bodu A bude známy, ak budeme poznať v každom časovom okamihu jeho polohu, t.j. budeme poznať závislosť polohového vektora ako funkciu času

r = r(t) (2.1.39)

Polohový vektor r vo zvolenej sústave je určený tromi súradnicami r = [x,y,z] . Nech na začiatku pohybu (v čase t = 0) je poloha bodu A určená polohovým vektorom r₀ so súradnicami r₀= [x₀,,y₀,,z₀]. Pohyb bodu A je známy, ak poznáme ako sa menia jednotlivé súradnice s časom v každom časovom okamihu, t.j. ak poznáme tri skalárne rovnice

x = x(t), y =y(t) , z = z(t) (2.1.40)

Pohybové rovnice bodu pri rovnomernom priamočiarom pohybe v priestore majú tvar:

x = x ₀+ v_x t y = y ₀+ v_y t z = z ₀+ v_z t (2.1.41)

kde pre veľkosť vektora rýchlosti, určeného súradnicami v_x, v_y , v_z platí

(2.1.42)

Rozdiel x –x₀ = v_xt udáva priemet trajektórie rovnomerného priamočiareho pohybu do osi x , resp. rozdiel y - y ₀= v_yt do osi y a rozdiel z - z ₀= v_z t do osi z. Dĺžka trajektórie Ds, ktorú hmotný bod pri rovnomernom priamočiarom pohybe za čas t opíše, je určená rovnicou

(2.1.43)

V prípade, že skúmame pohyb v rovine, jedna zo súradníc bodu A je nulová. (Ak sa jedná o rovinu xy, z-ová súradnica sa rovná nule, z = 0.) K stanoveniu rovnomerného pohybu potrebujeme poznať v každom časovom okamihu dve skalárne rovnice.

Najjednoduchší prípad nastane ak až dve súradnice sú nulové (napr. y = 0 a z = 0) t.j. hmotný bod sa pohybuje v smere tretej súradnicovej osi (v nami zvolenom prípade to bude os x). Tento prípad je však ekvivalentný s pohybom v nami už uvedenom prípade pohybu po priamke, určenej jednotkovým vektorom t.

_____________________________________