2.5.5 Zákon zachovania mechanickej energie v gravitačnom poli

            Keď hmotný bod m v gravitačnom poli bodu M uvoľníme, dá sa vplyvom pôsobenia gravitačných síl do zrýchleného pohybu smerom k zdroju poľa. Predpokladajme, že pri tomto pohybe má v bode 1 svojej dráhy potenciálnu energiu E_p1, v bode 2 potenciálnu energiu E_p2. V bode 1 má rýchlosť v₁ a teda kinetickú energiu E_k1, v bode 2 je jeho rýchlosť v₂ a kinetická energia E_k2 (obr.2.5.5.1 )

 

 

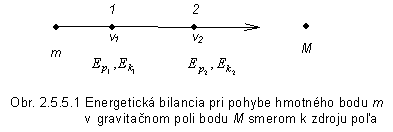
V predchádzajúcej časti sme ukázali, že  práca potrebná na prenos hmotného bodu z miesta 1 do miesta 2 je rovná rozdielu potenciálnych energií v týchto miestach, t.j.

 

                                                                                                   (2.5.5.1)

 

Z dynamiky zároveň vieme, že ak sa za účinku sily mení rýchlosť hmotného bodu, sila vykoná prácu rovnú rozdielu kinetických energií v týchto miestach, t.j.

 

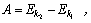                                                                                                    (2.5.5.2)

takže

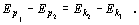                                                                                                     (2.5.5.3)

 

Posledný vzťah môžeme prepísať aj do tvaru

 

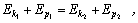                                                                                                      (2.5.5.4)

alebo

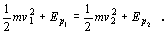                                                                                  (2.5.5.5)                       

 

Tento zápis matematicky vyjadruje zákon o zachovaní mechanickej energie: pri pohybe  voľného hmotného bodu (resp. telesa) v gravitačnom  poli sa jeho celková mechanická energia, daná súčtom kinetickej a potenciálnej energie, nemení.

            Príkladom je aj voľný pád telesa (resp. jeho zvislý vrh nadol alebo nahor) v gravitačnom poli Zeme.

 

Kontrolné otázky k časti 2.5.5

 

1.     Vyjadrite slovne aj matematicky zákon zachovania mechanickej energie pre pohyb hmotného bodu v gravitačnom poli.

2.     Uveďte príklady zachovania mechanickej energie pri pohybe telesa v gravitačnom poli Zeme.