2.5.2 Gravitačné sily. Newtonov gravitačný zákon

Ako prvý sa skúmaním gravitačných síl vážnejšie zaoberal ešte v 17. stor. anglický fyzik Isaac Newton. Je známa jeho príhoda s padajúcim jablkom, ktorá ho priviedla na myšlienku, že sila nútiaca padať telesá zvislo k Zemi je totožná so silou, ktorá núti obiehať planéty po obežných dráhach okolo Slnka, aj Mesiac okolo Zeme. V tom čase už boli známe zákonitosti pohybu planét, ktoré objavil nemecký astronóm Johannes Kepler. Newton v snahe vysvetliť tieto zákonitosti matematicky formuloval  gravitačný zákon,  podľa ktorého dve telesá s hmotnosťami m₁ a m₂ sa navzájom priťahujú silou F, ktorá je úmerná súčinu ich hmotností a nepriamo úmerná druhej mocnine ich vzájomnej vzdialenosti r. Matematicky možno tento zákon zapísať ako

   

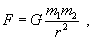                                                                                         (2.5.2.1)

 

kde G =  6,670 . 10^-11  N.m².kg^-2 je univerzálna gravitačná konštanta.

            Rovnica 2.5.2.1 platí presne len pre  hmotné body a pre homogénne gule, u ktorých za r dosadzujeme vzdialenosť ich stredov. S veľkou presnosťou ho môžeme použiť aj pre objemové telesá, ktorých rozmery sú zanedbateľné voči ich vzájomnej vzdialenosti; za r vtedy dosadzujeme vzdialenosť ich ťažísk. Pokiaľ teda v ďalšom texte na niektorých miestach  použijeme miesto pojmu „hmotné body“ pojem „telesá“ budú sa tu rozumieť práve takéto prípady (napr. pri popise gravitačného poľa Zeme).

Vzťah (2.5.2.1) môžeme prepísať do vektorového tvaru nasledovne:

            Nech poloha telesa s hmotnosťou m₂ voči telesu s hmotnosťou m₁ je daná polohovým vektorom r_1,2 (obr.2.5.2.1) a  r je absolútna hodnota tohto vektora. Silu F_1,2, ktorou pôsobí hmotný bod s hmotnosťou m₁ na hmotný bod s hmotnosťou m₂ dostaneme, ak jej absolútnu hodnotu násobíme jednotkovým vektorom v jej smere. Tento jednotkový vektor (vzhľadom na to, že gravitačná sila je príťažlivá a má opačný smer  ako vektor r_1,2) môžeme vyjadriť výrazom  

 

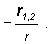
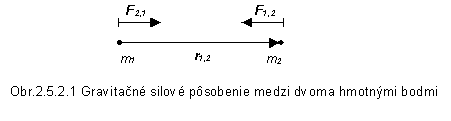
Pre silu F_1,2  takto dostávame            

                                                                                                      (2.5.2.2)

Obdobne  platí, že druhé teleso pôsobí na prvé rovnako veľkou, ale opačne orientovanou silou

 

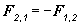                .                                                                                                   (2.5.2.3)

 

Východiskom pre Newtonove odvodenie boli Keplerove zákony , opisujúce pohyby planét v Slnečnej sústave.

           

Princíp Newtonovho postupu bol taký, že zo známych rovníc dráh planét určil silu, ktorá ich pohyb spôsobuje. Východiskom pri jeho pokusoch bol predovšetkým 3. Keplerov zákon. Takáto konštrukcia odvodenia je aj bežne uvádzaná vo väčšine  učebníc fyziky.

Uvedený časový postup je však daný historickými  súvislosťami a v skutočnosti by mal byť opačný. Keďže Newtonov gravitačný zákon má univerzálnejší charakter, mal by byť tento považovaný za východiskový a Keplerove zákony by  mali vyplývať z neho.

            V tomto module si preto ukážeme opačný spôsob, t.j. odvodenie Keplerových zákonov z Newtonovho gravitačného zákona.

 

Meranie gravitačnej konštanty G  uskutočnil ako prvý r. 1797 Henry Cavendish pomocou torzného kyvadla. 

 

 

Kontrolné otázky k časti 2.5.2

 

1.       Ktorý prípad planetárneho pohybu – okrem obiehania planét okolo Slnka  a družíc  okolo planét – ešte poznáte? Na základe akých  síl prebieha a prečo sa tu nemôžu uplatniť gravitačné sily?

2.       Vysvetlite, prečo sa predmety okolo nás – napr. nábytok v miestnosti – k sebe nepohybujú, aj keď sa navzájom priťahujú gravitačnými silami.

3.       Do  akej miery je správny predpoklad, že  pri popise gravitačných síl medzi telesami   si môžeme všetku hmotu telies predstaviť  sústredenú v ich ťažiskách, a na ne vzťahovať výpočty?

4.       Zdôvodnite, prečo Cavendish nazval svoj experiment „ váženie Zeme a Slnka.“ Vysvetlite, ako možno  určiť  hmotnosti Zeme a Slnka, keď poznáme vzdialenosti a obežné doby ich prirodzených družíc (t.j. Mesiaca a Zeme) a gravitačnú konštantu G.