Príklady:

 

Niektoré gravitačné konštanty a veličiny, ktoré budeme pri riešení príkladov potrebovať:

 

      Univerzálna gravitačná konštanta G = 6,67.10^-11 N.m².kg^-2

          Tiažové zrýchlenie na povrchu Zeme g = 9,81 m.s^-2

      Polomer Zeme (stredný) R_z = 6 378 km

      Hmotnosť Zeme M_Z = 5, 98.10²⁴ kg 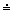 6.10²⁴ kg

      Polomer Mesiaca R_M= 1738 km 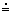 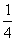 polomeru Zeme

      Vzdialenosť (stredná) Mesiaca od Zeme d_M = 384 400 km

      Polomer slnka R_S = 696 000 km

      Hmotnosť slnka M_S = 1,98.10³⁰ kg 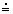2.10³⁰ kg

      Vzdialenosť (stredná) Slnka od Zeme d_S = 149 600 000 km 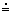 150.10⁶ km

 

1.  Aký je pomer tiaže telesa v najvyššom bode zemského povrchu (Mount Everest – nadmorská výška 8847 m) k tiaži telesa na úrovni hladiny mora? [0,997]

2.  Aká je hodnota tiažového zrýchlenia vo výške 10 000 km nad povrchom Zeme?      [1,49 m.s^-2]

3.  V akej výške nad povrchom Zeme je hodnota tiažového zrýchlenia polovičná vzhľadom na  zrýchlenie na povrchu Zeme ? [2 655 km]

4.  Raketa s hmotnosťou  1 000 kg vystúpila do výšky 3 000 km nad povrch Zeme. Akú prácu  vykonali raketové motory, keď predpokladáme, že gravitačné pole Zeme je a) homogénne s intenzitou 9,81 N.m^-1

       b) nehomogénne, t.j. intenzita sa mení so vzdialenosťou od povrchu Zeme ( v zmysle Newtonovho gravitačného zákona).[a)4,9.10⁹J ;b) 4,56.10⁹J]

5.    Určte hodnoty intenzity a potenciálu  gravitačného poľa Zeme

       a) na jej povrchu

       b) vo výške 1 000 km nad povrchom.

       [a) 9,81 N.m^-1; -6,27 . 10⁷ J.kg^-1; b) 7,35 N.m^-1; - 5,42 .10⁷ J.kg^-1 ]

6.  Akou rýchlosťou treba vrhnúť zo zemského povrchu v smere zvislo nahor teleso, aby  dosiahlo výšku rovnajúcu sa zemskému polomeru?

      (Odpor vzduchu zanedbajte). [7,9 km.s^-1]

7.  Do akej  vzdialenosti od povrchu  Zeme sa  vzdiali  teleso  vrhnuté zvislo  nahor  rýchlosťou 5 000 m.s^-1 ? Akú rýchlosť bude mať vo výške 1 000 km?

      [1592 km; 2828 m.s-¹]

1.      Akou rýchlosťou dopadne na Zem teleso, keď ho vo výške 2 000 km nad povrchom

a) voľne pustíme

b)  vrhneme zvislo nadol počiatočnou rýchlosťou 100 m.s^-1?  (Odpor vzduchu zanedbajte).

       [a) 5 473 m.s^-1; b) 5 495 m.s^-1]

9.   Aká je vzdialenosť Marsu od Slnka, keď vieme, že doba jedného obehu Marsu je 687 dní?  [387 mil. km]

10.  Určte obežnú rýchlosť

      a) Mesiaca pri obiehaní okolo Zeme

      b) Zeme pri obiehaní okolo Slnka

      c) stacionárnej družice Zeme.

      [a) 1,02 km.s^-1; b) 29,8 km.s^-1; c)3,33 km.s^-1]

11. Aká je rýchlosť  a doba jedného obehu umelej družice Zeme, obiehajúcej po kruhovej  dráhe vo výške 3 000 km nad povrchom Zeme? [6,53 km.s^-1; 2,5 hod.]

12. V akej výške a s  akou  obvodovou a uhlovou rýchlosťou obieha okolo Zeme družica  s dobou obehu 2 hod. [1692 km; 7 km.s^-1; 0,87 mrad. s^-1]

13. Koľko obehov vykoná za 1 deň umelá družica Zeme, obiehajúca po kruhovej dráhe  vo výške 1000 km nad povrchom Zeme? [13,7]

14. Aký je  pomer tiaže telesa na povrchu Mesiaca k jeho  tiaži na povrchu Zeme? [1:6]

15.    V ktorom mieste na priamej spojnici medzi Zemou a Mesiacom nastane situácia,

      a)  že intenzita  spoločného gravitačného poľa je rovná nule

      b) potenciál poľa Zeme sa   rovná  potenciálu poľa Mesiaca

      [a) 345 600 km; b) 379 317 km od stredu Zeme]

16. Keby mal byť Mesiac udržiavaný na obežnej dráhe okolo Zeme oceľovým lanom miesto  gravitácie, aký by musel byť priemer lana, keď ťažné napätie lana nesmie prekročiť hodnotu s  = 2.10³  N.mm^-2? [357 km]

17.  Vypočítajte hodnoty I. a II. kozmickej rýchlosti pre Mesiac. [1,7 km.s^-1; 2,4 km.s^-1]

18.  Vypočítajte výšku obiehania stacionárnej družice Mesiaca nad jeho povrchom. [88 403 km]

19.  Akou minimálnou rýchlosťou treba vystreliť raketu zo Zeme, aby dopadla na Mesiac?

       Akou  rýchlosťou pritom  dopadne  na  Mesiac?  ( Pri výpočte použite odvodenia   z príkladu 15).