2.5.7 Gravitačné pole Zeme
Naša
planéta Zem tiež vytvára vo svojom okolí gravitačné pole. Môžeme predpokladať,
že Zem má tvar homogénnej gule s hmotnosťou Mz 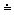 6.1024
kg, s polomerom Rz = 6 378 km. Spomínali sme
už, že gravitačné pole v okolí homogénnej gule je rovnaké ako v okolí
hmotného bodu s rovnakou hmotnosťou, nachádzajúceho sa v strede gule.
6.1024
kg, s polomerom Rz = 6 378 km. Spomínali sme
už, že gravitačné pole v okolí homogénnej gule je rovnaké ako v okolí
hmotného bodu s rovnakou hmotnosťou, nachádzajúceho sa v strede gule.
Pod
pojmom tiaž telesa rozumieme silu, ktorou je teleso o hmotnosti m priťahované k Zemi. Označujeme ju
symbolom Fg a môžeme
ju vyjadriť pomocou Newtonovho zákona sily a (ak neuvažujeme nepatrný vplyv
rotácie Zeme) aj pomocou Newtonovho
gravitačného zákona. V skalárnom tvare to je

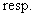
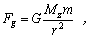 (2.5.7.1)
(2.5.7.1)
kde r predstavuje
vzdialenosť telesa od stredu Zeme a g
je zrýchlenie telesa, ktoré mu udeľuje gravitačná sila – tzv. tiažové zrýchlenie (pri zanedbaní vplyvu
rotácie Zeme je totožné
s gravitačným zrýchlením, zavedeným v časti 2.5.3). Ako vyplýva z uvedených vzťahov, toto
zrýchlenie môžeme vyjadriť ako
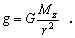 (2.5.7.2)
(2.5.7.2)
Pre povrch Zeme, kde r = Rz, je tiažové zrýchlenie rovné
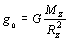 (2.5.7.3)
(2.5.7.3)
a má hodnotu približne 9,81 m.s-2 (presná
hodnota závisí od zemepisnej šírky).
Potenciálna energia telesa vo
vzdialenosti r od silového centra, t.j. od stredu Zeme je daná vzťahom
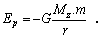 (2.5.7.4)
(2.5.7.4)
V praxi je však mnohokrát vhodnejšie vzťahovať
ju vzhľadom na zemský povrch. Jednoduchým výpočtom môžeme ukázať, že pre
relatívne malé výšky h nad povrchom
Zeme, kde môžeme hodnotu tiažového zrýchlenia
považovať za konštantnú (a teda pole za homogénne) sa uvedený vzťah
zjednoduší na tvar Ep = mgh, známy
z dynamiky.
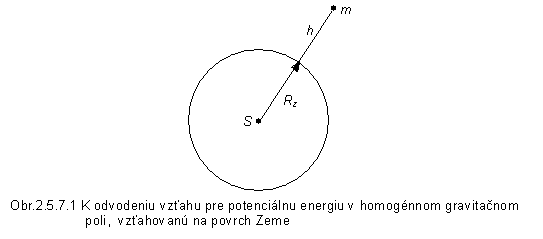
Ako je
zrejmé z obr. 2.5.7.1, potenciálnu energiu v určitom bode vo
výške h vzťahovanú na povrch Zeme
môžeme vyjadriť ako rozdiel energií v danom bode a na zemskom povrchu
(obe voči nekonečnu)
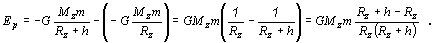 (2.5.7.5)
(2.5.7.5)
Ak uvážime, že h
<<Rz, dostaneme
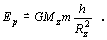 (2.5.7.6)
(2.5.7.6)
Po aplikovaní vzťahu (2.5.7.2), podľa ktorého
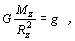
dospejeme k výsledku
Ep
= m g h . (2.5.7.7)

Príklad 2.5.7.1
Aká je hodnota tiažového
zrýchlenia g vo výške h = 100 km nad povrchom Zeme?
Riešenie:
Tiažové zrýchlenie g v danom mieste poľa je rovné intenzite poľa
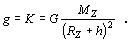 (2.5.7.8)
(2.5.7.8)
Číselne pre danú výšku dostaneme
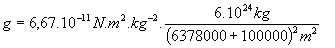 (2.5.7.9)
(2.5.7.9)
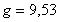 m.s-2
m.s-2
Vypočítaná hodnota sa líši od hodnoty zrýchlenia na povrchu Zeme menej
ako o 3 %. Gravitačné pole po úroveň takýchto relatívne „malých“ výšok
môžeme pokladať za homogénne, s konštantnou hodnotou intenzity (resp.
zrýchlenia) 9,81 m.s-2.

Dôležitými veličinami pre každé väčšie
nebeské teleso (Slnko, planéty, mesiace) sú I. a II. kozmická rýchlosť. Určíme
teraz ich hodnoty pre planétu Zem:
I.
kozmická rýchlosť 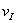 je rovná rýchlosti,
ktorú musíme udeliť telesu v horizontálnom smere tesne nad povrchom Zeme,
aby obiehala okolo nej po kruhovej dráhe ako umelá družica Zeme.
je rovná rýchlosti,
ktorú musíme udeliť telesu v horizontálnom smere tesne nad povrchom Zeme,
aby obiehala okolo nej po kruhovej dráhe ako umelá družica Zeme.
II.
kozmická rýchlosť vII
predstavuje tzv. únikovú rýchlosť z povrchu Zeme. Je to minimálna
rýchlosť, ktorou musíme vrhnúť teleso
zo zemského povrchu zvislo nahor, aby
natrvalo opustilo gravitačné pole Zeme a viac sa nevrátilo, t.j. vzdialilo sa
do nekonečna.

Príklad 2.5.7.2:
Určte výšku h
nad povrchom Zeme, v akej obiehajú stacionárne družice.
Riešenie:
Stacionárne družice Zeme sú
také umelé družice, ktoré obiehajú nad zemským rovníkom v smere od západu na
východ, pričom doba ich obehu je zhodná
s dobou jedného otočenia Zeme okolo svojej osi, t.j. T = 24 hod.= 86400 s. Takáto družica sa potom zdá akoby „zavesená“
nad jedným miestom zemského povrchu. Stacionárne družice sú preto veľmi vhodné
na telekomunikačné účely, t.j. na prenos rozhlasových a televíznych programov,
medzikontinentálnych telefonických hovorov a pod.
Pri výpočte výšky h
vychádzame z rovnosti fiktívnej odstredivej sily a dostredivej, t.j.
gravitačnej sily
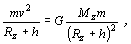
kde rýchlosť obiehania v
určíme ako podiel dráhy a času pri jednom obehu
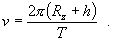
Po dosadení do predchádzajúceho vzťahu a vykrátení hmotnosti m na oboch stranách rovnice dostaneme
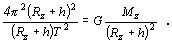
Po úprave
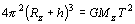
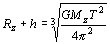

a číselne
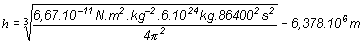
h = 35 900 km
Poznámka: Odstredivú silu môžeme vyjadriť aj pomocou uhlovej rýchlosti w. Výhodou tohto vyjadrenia je, že uhlová rýchlosť družice je rovnaká
ako u bodov na zemskom povrchu. Tento spôsob riešenia prenechávame na čitateľa.

Kontrolné otázky k časti 2.5.7
1. Ktoré
planéty – okrem Zeme – tvoria planetárny systém Slnečnej sústavy?
2. Čo je to
tiaž telesa? S ktorou silovou interakciou súvisí?
3. Je tiažové
zrýchlenie na povrchu Zeme totožné s gravitačným zrýchlením? (Pri zdôvodnení vezmite do úvahy rotáciu Zeme okolo svojej osi).
4. Definujte
I. a II. kozmickú rýchlosť.
5. Aký tvar
bude mať dráha telesa , ktorému tesne nad povrchom Zeme udelíme v horizontálnom smere rýchlosť (odpor
vzduchu zanedbávame)
a) menšiu ako
I. kozmická rýchlosť
b) rovnú I.
kozmickej rýchlosti
c) väčšiu ako
I. kozmická rýchlosť, ale menšiu ako II. kozmická rýchlosť (t.j. rýchlosť
v intervale 7,9 až 11,2 km.s-1)
d) rovnú alebo
väčšiu ako II. kozmická rýchlosť
6. Čo je to
stacionárna družica?
7. Pomocou
gravitačnej teórie vysvetlite javy morského prílivu a odlivu.