4.2.3 Termodynamické procesy

 

            Na opis rovnovážneho stavu sústavy častíc sa používajú stavové veličiny, ktorých vzájomný súvis vyjadruje stavová rovnica.

V sústave prebiehajúce procesy môžeme rozdeliť z hľadiska ich vratnosti na:

·     reverzibilné ( vratné ) procesy - po prebehnutí takéhoto procesu sa sústava môže sama, bez vonkajšieho vplyvu, dostať späť do východiskového stavu. Takým procesom je napríklad veľmi pomalá expanzia plynu uzavretého v nádobe s pohyblivou stenou. A potom opačný proces, veľmi pomalá kompresia tohoto plynu do pôvodného stavu. Proces musí byť tak pomalý, že plyn sa dostáva z počiatočného do konečného stavu a opačne sledom rovnovážnych stavov, ktoré plyn dosahoval po nekonečne malých zmenách týchto rovnovážnych stavov.

·      ireverzibilné ( nevratné ) procesy - sústava sa nemôže sama, bez vonkajšieho vplyvu, dostať späť do východzieho stavu. Príkladom takéhoto procesu môže byť prudké stlačenie alebo expanzia plynu v nádobe.

Tieto procesy môžu v prírode prebiehať za rôznych špecifických podmienok.

a)  Opíšeme proces prebiehajúci v sústave uzavretej v nádobe s konštantným objemom - izochorický dej. Všeobecne platí, že ak dodáme sústave teplo dQ, toto teplo sa rozdelí na časť dU, ktorá spôsobí zvýšenie vnútornej energie a časť 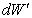, ktorou vykoná plyn prácu. Teda platí

 

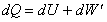                                                                                        (4.2.3.1 )

 

Elementárnu zmenu vnútornej energie v tomto vzťahu, množstva n mólov plynu pri zmene teploty o dT, môžeme zapísať 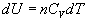a plynom vykonanú prácu pri zmene objemu o dV vzťahom dW¢ = pdV. Potom prejde vzťah 4.2.3.1 do tvaru

 

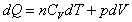.                                                                                    ( 4.2.3.2 )

 

Za danej podmienky, že objem je konštantný (V = konšt.) je zmena objemu nulová (dV = 0 ), teda aj práca vykonaná plynom je nulová (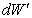= 0 ). Potom sa teplo dodané sústave prejaví len zmenou vnútornej energie. Ak ešte za látkové množstvo dosadíme

,

 

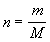vzťah 4.2.3.1  nadobudne tvary

 

 

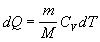
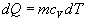
                                  ( 4.2.3.3 )

 

.

 

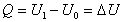Poslednú rovnicu môžeme slovne vyjadriť takto: Teplo dodané sústave pri izochorickom deji spôsobí len zmenu jej vnútornej energie.

 

b)  Proces prebiehajúci v sústave pri konštantnej teplote - izotermický proces.

Pri sledovaní tohoto procesu budeme vychádzať zo vzťahu 4.2.3.2  .

Za danej podmienky, že teplota je konštantná (T = konšt.) je zmena teploty nulová (dT = 0 ), teda aj zmena vnútornej energie je nulová (dU = 0 ). Potom teplo dodané sústave, sa prejaví ako práca plynu, ktorú vykoná pri svojej expanzii. Rovnica 4.2.3.2 prejde do tvaru

 

 

 

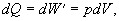
alebo

.

 

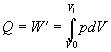Ak za tlak plynu dosadíme upravenú rovnicu Boylovho - Mariottovho zákona v tvare

 

,

 

platí

  .

 

Rovnica opisuje výpočet práce pri známych zmenách hodnôt tlaku a objemu plynu.Túto prácu je možné vypočítať využitím posledného vzťahu aj pri zadaní iných stavových veličín, využitím vhodného tvaru stavovej rovnice. Napríklad

 

·   ,

 

·   ,

 

·   ,

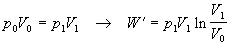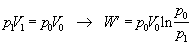a podobne.

 

c)  Proces pri konštantnom tlaku - izobarický proces.

Za danej podmienky, že tlak je konštantný (p = konšt.) je aj jeho zmena nulová (dp = 0 ). Potom, teplo dodané sústave sa prejaví zvýšením vnútornej energie a prácou, ktorú plyn vykoná pri svojej expanzii. Rovnicu 4.2.3.2 môžeme napísať v tvare

,

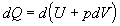alebo

.

 

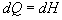V poslednom vzťahu sme označili H = U + pV, kde H sme označili novozavedenú fyzikálnu veličinu nazvanú entalpia sústavy. Jeho integráciou dostaneme

 

  .

 

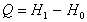Slovne: Teplo prijaté sústavou za konštantného tlaku sa rovná prírastku entalpie sústavy.

 

d) Proces prebiehajúci bez výmeny tepla medzi sústavou a okolím - adiabatický proces. V prírode sa vyskytujúce procesy, ktoré prebiehajú dostatočne rýchlo môžeme považovať za adiabatické.

Za danej podmienky, že teplo dodané sústave je nulové (dQ = 0 ), rovnica 4.2.3.1 nadobúda tvar

 

,

alebo

.                                                                                       ( 4.2.3.4 )

 

Nájdime teraz diferenciály oboch strán stavovej rovnice pV = nRT  za podmienky, že n,R sú konštanty a vyjadrime z nej diferenciál teploty

 

 

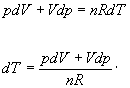
Dosadením do rovnice 4.2.3.4  za dT upravíme vzniknutý vzťah jednoduchými matematickými úpravami

 

 

 

 

 

.

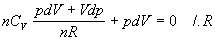
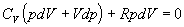
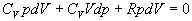
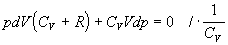
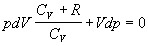
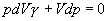Poslednú úpravu sme vykonali využitím platnosti rovnice

 

,

 

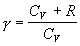 paragraf 4.1.5. Ďalej vykonáme separáciu premenných a  rovnicu zintegrujeme ako neurčitý integrál

 

 

,

 

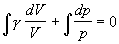
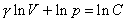kde ln C je zvolená integračná konštanta. Využijeme poznaty z matematiky o odlogaritmovaní a dostávame

 

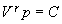.                                                                                                      ( 4.2.3.5 )

 

Vzťah 4.2.3.5  nazývame Poissonova rovnica. Udáva vzájomnú závislosť tlaku a objemu plynu pri adiabatických zmenách.

Vzťah môžeme napísať aj v nasledujúcom tvare

 

 

 

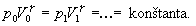
Grafickú závislosť tlaku a objemu pri adiabatickom deji a na porovnanie aj pri izotermickom deji znázorňuje obr. 4.2.3.4.

 

 


Príklad 4.2.3.1

Akú hmotnosť má hélium ( molárna hmotnosť M = 4.10-3 kg.mol-1 ), ktoré sme zohriali dodaním tepla 209 J z teploty 60 0C na 80 0C pri konštantnom objeme ?

 

Riešenie :

V súlade so zadaním označíme Q = 209 J, t1 =  60 0C a t2 =  80 0C. Pre výpočet použijeme vzťah 4.2.3.3 v tvare

 

.

 

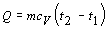Úpravou Mayerovho vzťahu 4.2.2.3 získame vzťah pre výpočet cV :

 

 

 

 

 

.

 

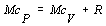
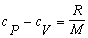
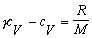
Pri úprave sme využili vzťah pre výpočet Poissonovej konštanty 4.1.14 . Po dosadení do východzieho vzťahu dostávame :

 

 .

 

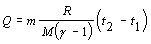Vzťah matematicky upravíme a dosadíme číselné hodnoty. Hodnotu Poissonovej konštanty vypočítame využitím empirického vzťahu 4.1.14, pričom zo zadania príkladu vieme, že počet stupňov voľnosti i = 3. Prevod teploty z Celziovej na Kelvinovu sme urobili ako v príklade 4.2.1.2 .

 

 .

 

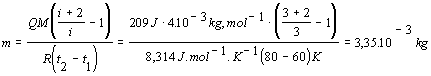Za daných podmienok sme zohriali 3,35.10-3 kg hélia.