4.2.2 Tepelné kapacity látok, skupenské teplá

Majme telesá z rôznych druhov látok napr. kvapalné teleso - destilovaná voda v nádobe, plynné teleso - kyslík v balóne, tuhé teleso - medená kocka, ... , všetky rovnakej hmotnosti. Pokusom by sme zistili, že hoci majú telesá hmotnosť rovnakú, na zvýšenie ich teploty o rovnakú hodnotu za rovnakých vonkajších podmienok je potrebné rôzne množstvo tepla. Vlastnosť, ktorou sa tieto telesá od seba navzájom odlišujú a ktorú sme pokusom prezentovali nazývame tepelná kapacita telies.

V paragrafe 4.1.5 sme sa zaoberali tepelnou kapacitou ideálneho plynu, pričom sme zistili, že tepelnú kapacitu je potrebné sledovať aj v závislosti od podmienok, za akých dodávame plynu teplo. Podľa toho rozlišujeme tepelnú kapacitu pri konštantnom tlaku a pri konštantnom objeme.

Tieto kapacity sme vztiahli na jeden kilogram látky, čím sme zaviedli hmotnostnú tepelnú kapacitu  c_p, c_V, alebo na jeden mól látky, čím sme zaviedli molárne tepelné kapacity C_p  C_V . Podobne zavádzame aj tepelné kapacity pre kvapaliny a tuhé látky.

            Teraz zistíme, aký je vzťah medzi kapacitami C_p a  C_V.

   

Využijeme prvú vetu termodynamickú (vzťah 4.2.1.3), ktorú dosadíme do definičného vzťahu pre molárnu tepelnú kapacitu a dodávku tepla sústave uskutočníme v dvoch krokoch. Najskôr vykonáme zmenu izochorickú - nedovolíme plynu meniť objem a dej opíšeme rovnicou

 

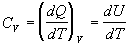 ,                                                                                               ( 4.2.2.1 )

kde sme využili

 

,

 

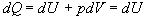lebo (dV = 0) a zápis

 

 

 

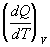
nám hovorí, že teplo bolo sústave dodané za konštantného objemu.

V ďalšom kroku piest uvoľníme, plyn expanduje, ochladí sa a my mu dodáme teplo, aby sa jeho teplota zvýšila na pôvodnú hodnotu. Pri veľmi pomalom pohybe piesta je v rovnováhe tlak vnútri nádoby s tlakom mimo nádoby - prebieha izobarický dej, ktorý opíšeme rovnicou

 

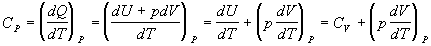.                     ( 4.2.2.2 )

 

Pri úpravách sme využili vzťahy 4.2.1.3 a 4.2.2.1 .

Ďalej vykonajme deriváciu stavovej rovnice ideálneho plynu pri konštantnom tlaku

 

             .

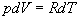Jej úpravou získame vzťah

 

             ,

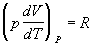ktorý dosadíme do rovnice 4.2.2.2. Tak dostávame

 

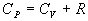             .                                                                                                          ( 4.2.2.3 )

 

Túto rovnicu nazývame Mayerov vzťah, ktorý vyjadruje súvislosť medzi molárnymi tepelnými kapacitami pri stálom tlaku a stálom objeme prostredníctvom univerzálnej plynovej konštanty R. Zároveň z nej vidno význam molárnej plynovej konštanty R. Tá sa číselne rovná práci, ktorú vykoná jeden mól plynu pri jeho zohriatí o 1 K (1 °C) pri konštantnom tlaku. Zohriatím jedného mólu plynu pri konštantnom objeme sa všetko privedené teplo využije na zvýšenie jeho vnútornej energie. Pri zohrievaní za konštantného tlaku sa objem plynu musí zväčšiť, teda plyn koná prácu, na ktorú sa mu musí dodať ďalšie teplo, ktorého množstvo sa číselne rovná práve molárnej plynovej konštante R .

            V predošlom texte sme sa zaoberali látkami plynnými. Ak by sme hovorili o látkach  tuhých a kvapalných, pod pojmom hmotnostná tepelná kapacita sa obyčajne rozumie hmotnostná tepelná kapacita pri konštantnom tlaku. Táto sa od hodnoty pri konštantnom objeme líši len o veľmi malú hodnotu. Preto pri riešení praktických úloh vo väčšine prípadov nie je potrebné tento rozdiel brať do úvahy.

            Zo skúsenosti vieme, že niektoré látky (napr. H₂O), sa bežne vyskytujú vo viacerých skupenstvách. Tuhé skupenstvo - ľad, kvapalné skupenstvo - voda, plynné skupenstvo - vodná para. Dodávaním tepla chemicky čistej látke v skupenstve tuhom sa zvyšuje jej teplota až na hodnotu nazývanú teplota topenia. Pri tejto teplote začína látka meniť svoje skupenstvo z tuhého na kvapalné. Teplo dodávané sústave pri tejto teplote sa spotrebováva na zmenu skupenstva, pričom teplota sústavy je stále konštantná, dokedy sa nezmení všetka tuhá látka na kvapalnú. Toto teplo nazývame skupenské teplo topenia a vypočítame ho

 

,

 

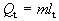kde : m  je hmotnosť látky,  l_t  je hmotnostné skupenské teplo topenia danej látky.

Hmotnostné skupenské teplo topenia látky je množstvo tepla, ktoré je potrebné dodať tuhej látke s jednotkovou hmotnosťou, zohriatej na teplotu topenia, aby zmenila svoje skupenstvo na kvapalné s tou istou teplotou. Podobne je definované skupenské teplo a hmotnostné skupenské teplo tuhnutia látky, pričom sa jedná o zmenu skupenstva kvapalného na tuhé.

            Ďalším dodávaním tepla kvapalnej látke rastie jej teplota až na hodnotu, pri ktorej sa začne látka vyparovať v celom svojom objeme. Túto teplotu nazývame teplota varu. Látka mení svoje skupenstvo z kvapalného na plynné, pričom teplota sústavy sa nemení. Všetko teplo dodané látke pri tejto teplote sa spotrebuje na jej vyparenie a nazýva sa skupenské teplo vyparovania látky. Vypočítame ho

 

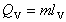,                                                                                                     ( 4.2.2.4 )

 

kde : m  je hmotnosť látky,  l_v  je hmotnostné skupenské teplo vyparovania danej látky.

Hmotnostné skupenské teplo vyparovania látky je množstvo tepla, ktoré je potrebné dodať kvapalnej látke s jednotkovou hmotnosťou, zohriatej na teplotu varu, aby zmenila svoje skupenstvo na plynné s tou istou teplotou. Podobne je definované skupenské teplo a hmotnostné skupenské teplo kondenzácie látky. Proces prebieha pri uvoľňovaní tepla zo sústavy a látka mení svoje skupenstvo z plynného na kvapalné.

            V prírode sa vyskytujú aj procesy zmeny látky zo skupenstva tuhého na plynné. Proces nazývame sublimácia látky a je možné opísať ho podobným spôsobom ako topenie a vyparovanie. Sublimáciu charakterizujeme skupenským teplom sublimácie a hmotnostným skupenským teplom sublimácie. Opačný proces, proces prechodu látky zo skupenstva plynného do skupenstva tuhého nazývame desublimácia.

            Jednotkou hmotnostného skupenského tepla topenia (tuhnutia) a jeho ekvivalentov pri vyparovaní a sublimácii je joule na kilogram [J.kg ^-1].

            Všetky premeny skupenstiev ktoré sme opísali, súvisia s tlakom. Čiže aj hodnoty skupenských a hmotnostných skupenských tepiel závisia od tlaku. Nami opísané procesy sme sledovali pri konštantnom barometrickom tlaku.

 

Príklad 4.2.2.1

Vypočítajte hodnotu Poissonovej konštanty γ zmesi plynov. Zmes tvorí m₁ = 3.10^-3 kg argónu a m₂ = 8.10^-3 kg kyslíka. Ďalej je známa molárna hmotnosť argónu M_A @ 40.10^-3 kg.mol^-1, kyslíka M_O1 = 32.10^-3 kg.mol^-1 a hmotnostná tepelná kapacita argónu 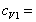319 J.kg^-1.K^-1 a kyslíka  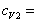648 J.kg^-1.K^-1.

 

Riešenie :

Pri riešení budeme vychádzať zo vzťahu 4.1.14 pre výpočet Poissonovej konštanty

 

 

 

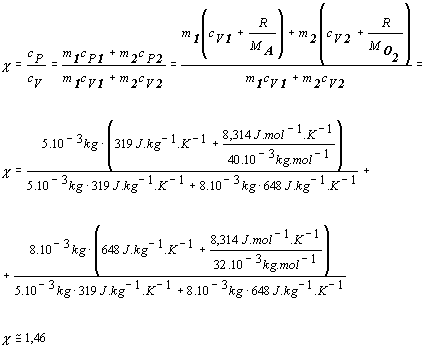
Pri výpočte sme nahradili c_P  Mayerovým vzťahom 4.2.2.3 upraveným nasledujúco:

 

 

 

.

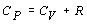
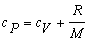Číselnú hodnotu konštanty R sme odčítali z tabuliek.

Hodnota Poissonovej konštanty pre danú zmes plynov je c @ 1,46.

 

Príklad 4.2.2.2

Kondenzátor chladiča prijíma paru s teplotou 100 ⁰C a mení ju na vodu s teplotou 40 ⁰C. Chladiacim médiom v kondenzátore je voda. V procese chladenia sa jej teplota zvýši z 10 ⁰C na 40 ⁰C. Koľko chladiacej vody je treba na každý kilogram pary?

 

Riešenie :

Celkové teplo, ktoré má chladiaca voda odobrať v procese chladenia môžeme rozdeliť na dve časti. Prvá bude tvoriť teplo Q₁ odobraté pare počas procesu jej kondenzácie. Toto teplo vypočítame podľa vzťahu 4.2.2.4

 

 ,

 

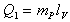kde m_P  = 1kg je hmotnosť pary.

Ďalším ochladzovaním odoberieme vode (kondenzovanej pare) teplej t₁ = 100 ⁰C teplo Q₂ , pričom sa ochladí na teplotu t₂ = 40 ⁰C. Toto teplo vypočítame ako teplo uvoľnené pri zmene vnútornej energie (zmena objemu je zanedbateľná) pri zmene teploty z t₁ na t₂ .

 

.

 

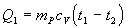Celkové uvoľnené teplo je

 

.

 

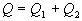Týmto teplom sa zohreje chladiaca voda z t₃ = 10 ⁰C na t₄ = 40 ⁰C, pričom jej hmotnosť musí byť m, teda

.

 

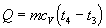Dosadíme za Q ,Q₁ a Q₂ a upravíme

 

 

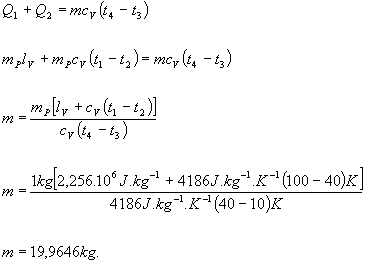
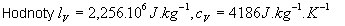
sme odčítali z tabuliek.

 

Na každý kilogram pary je treba 19,9646 kg chladiacej vody.