4.2 Termodynamika
Pojem termodynamika
bol zavedený už v dávnej minulosti na označenie časti fyziky
skúmajúcej premenu tepla na mechanickú prácu a javy prebiehajúce v plyne
s touto premenou spojené.
Termodynamika
pri opise javov priamo nevyužíva molekulovú štruktúru látok. Sleduje len
makroskopické zmeny, hoci tieto sú dôsledkom zmien mikroskopických. Ani po
vzniku vedných disciplín, ako je molekulová a štatistická
fyzika, sa význam termodynamiky nezmenšil. Tieto len upresnili formulácie
alebo hranice niektorých zákonov už dovtedy definovaných termodynamikou.
Preto, že termodynamika nepotrebuje údaje o molekulovej štruktúre,
môže často oveľa jednoduchšie opísať skúmané javy ako napríklad molekulová
alebo štatistická fyzika. Uplatnenie nachádza nie len v strojárskych
odboroch, ale aj v chémii, biológii a podobne.
4.2.1 Vnútorná energia plynov a prvá veta
termodynamická
Majme
častice podliehajúce vzájomnému pôsobeniu i pôsobeniu vonkajších síl. Takými
časticami sú častice tvoriace tuhé, kvapalné alebo plynné teleso. Označme Epij
- vzájomnú potenciálnu energiu medzi časticami i, j .
Celková vnútorná potenciálna
energia sústavy potom je
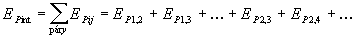 .
.
Celková vnútorná energia
sústavy
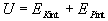 ,
,
kde : E Kint- je celková
vnútorná kinetická energia sústavy.
Podľa zákona zachovania
energie sa táto nemení, ak je sústava izolovaná.
Označme teraz
U0 - počiatočnú vnútornú energiu sústavy,
U1 - vnútornú energiu sústavy po skončení
pôsobenia vonkajších síl,
Wext - celkovú prácu vykonanú
vonkajšími silami.
Vonkajšia práca dodaná
sústave spôsobí zmenu jej vnútornej energie, čo môžeme napísať vzťahom
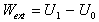 . (
4.2.1.1 )
. (
4.2.1.1 )
S ohľadom na prácu
vykonanú vonkajšími silami môžu nastať nasledujúce situácie:
·
Wext = 0 , potom U1 = U0 Þ vnútorná energia sústavy sa nemení,
·
Wext > 0 , potom U1 > U0 Þ vnútorná energia sústavy rastie,
·
Wext < 0 , potom U1 < U0 Þ vnútorná energia sústavy klesá.
Využijúc tretí Newtonov
zákon môžeme vzťah medzi prácou vonkajších síl a prácou vykonanou sústavou
označiť
Wext = - Wsús alebo aj W
= -W¢.
Vnútornú energiu sústavy možno
zmeniť dodaním:
a) mechanickej
práce
b) tepla.
Sledujme
teraz plyn uzavretý vo valci s pohyblivým piestom ako ukazuje obrázok
4.2.1.1, kde
S - je plošný obsah piesta,
F - je
veľkosť zložky výslednice síl nárazov častíc na piest spadajúcich do smeru
pohybu piesta,
F1 , F2 ,F3 , F4
, -
sú veľkosti síl vytvorené nárazom častíc plynu na steny nádoby,
dl - je
veľkosť elementu dĺžky posunutia piesta,
dV - je elementárna zmena objemu plynu pri jeho posunutí o dl.
K bodu a)
Zapíšme tlakovú silu plynu
vzťahom
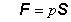 , (
4.2.1.2)
, (
4.2.1.2)
kde S je vektor
priradený ploche S a má smer kolmý na túto plochu. Plynom vykonaná práca
pri posunutí piesta o dl je
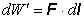 ,
,
kde dl je vektor elementu posunutia
piesta silou F. Po dosadení za F zo vzťahu 4.2.1.2 prácu vypočítame
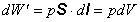 .
.
Ak zmeníme objem
z hodnoty V0 na V1 , celková práca vykonaná
plynom je
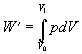 ,
,
a vonkajšia práca, práca
plynu dodaná je
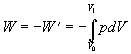 .
.
K bodu b)
Plynu
môžeme energiu dodať aj iným spôsobom.
Častice tvoriace látku
(atómy, molekuly, ióny, ...) konajú chaotický pohyb, ktorého prejavy ako prvý
pozoroval anglický botanik Brown, keď pod mikroskopom sledoval trhavý pohyb
peľového zrnka vo vode. Pohyb zrnka bol neskoršie vysvetlený ako dôsledok
nepravidelnosti nárazov častíc vody na zrnko. Takýto pohyb častíc látky (nielen
kvapalnej) pomenovali tepelný pohyb a
veličinu, ktorou ho môžeme navonok registrovať - teplota. Energiu plynu teda môžeme dodať aj prostredníctvom
interakcií jednotlivých častíc nepohyblivých stien nádoby, s časticami
plynu (konaním mikropráce), pričom dochádza k výmene energie medzi
časticami. Energia plynu bude dodaná len vtedy, ak energia častíc stien bude
vyššia, ako energia častíc plynu. Takto dodanú energiu nemôžeme vyjadriť
súčinom vonkajšej sily a dráhy a nazveme ju teplo.
Teplo dodané sústave zvonka
považujeme za kladné +Q, teplo
uvolnené sústavou považujeme za záporné -Q.
Celková energia dodaná sústave môže obsahovať obe zložky, teda
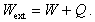
Ak sústava energiu okoliu
odovzdáva

Využitím poznatkov o
zachovaní energie ( vzťah 4.2.1.1 ), pre zmenu vnútornej energie platí
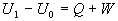 .
.
Toto matematické vyjadrenie
zákona zachovania energie nazývame prvá
veta termodynamická. Slovne : Prírastok
vnútornej energie sústavy sa rovná súčtu sústave dodaného tepla a dodanej
práce.
Ak vykonala prácu sústava,
môžeme prvú vetu termodynamickú napísať v tvare
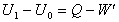 .
.
Vnútorná energia sústavy
závisí len od stavu sústavy, nie od spôsobu, akým sa doň dostala, veličiny W a Q
však sú závislé od spôsobu prechodu sústavy zo stavu U0 do U1
.
Je veľa spôsobov, ktorými sa
môže dostať sústava zo stavu U0
do U1 , ale U0 - U1 = DU nezávisí od spôsobu tohoto prechodu.
Pre extrémne malé zmeny U, Q a W nadobúda prvá veta termodynamická tvar
 . (
4.2.1.3 )
. (
4.2.1.3 )
Majme sústavu, ktorá prijala
od okolia a potom odovzdala okoliu prácu alebo teplo, pričom sa jej konečný
stav rovnal počiatočnému. Takémuto deju hovoríme kruhový dej.
Ak v ľubovoľnej sústave
prebehne ľubovoľný kruhový dej, sústavou prijatá energia sa rovná nule a prvú
vetu termodynamickú (vzťah 4.2.1.3) môžeme napísať v tvare
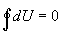 .
.
Toto vyjadrenie prvej vety
termodynamickej je v plnej zhode so zákonom zachovania energie.
Hodnota veličiny U závisí len od konečného a počiatočného
stavu, nie od spôsobu priebehu zmeny stavu. Takéto veličiny ( teda aj veličinu U ) nazývame stavové veličiny. (Pozri paragraf 4.2.6)

Príklad 4.2.1.1
Ako sa zmení
vnútorná energia plynu uzavretého v nádobe s pohyblivým piestom, ak
sa piest posunul priamočiaro a zväčšil svoj objem za stáleho tlaku p = 0,1 MPa z objemu V0 = 100 l na V1 = 150 l a zároveň
ohrievaním prijal plyn teplo Q = 10
kJ.
Riešenie :
Teplo dodané
plynu sa využije na vykonanie práce plynom a na zvýšenie jeho vnútornej
energie. Pri riešení využijeme prvú vetu termodynamickú, vzťah 4.2.1.3 ,
v tvare
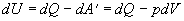 .
.
Obe strany
rovnice zintegrujeme v hraniciach stanovených zadaním a za podmienky
konštantného tlaku
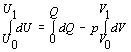
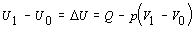
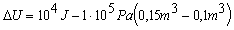
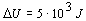 .
.
Vnútorná
energia plynu sa zvýši o 5.103
J.
Príklad 4.2.1.2
Aká je
hmotnosť kyslíka v nádobe, ak po dodaní tepla Q = 8kJ sa jeho teplota zvýšila z t1 = 10 0C na t2 = 70 0C.
Riešenie :
Teplo dodané
sústave spôsobilo zvýšenie vnútornej energie, čoho dôsledkom bolo aj zvýšenie
teploty plynu. Zmenu vnútornej energie plynu môžeme vypočítať aj ako rozdiel
dvoch rôznych stavov vnútornej energie plynu
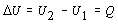 .
.
Využitím
poznatkov z molekulovej fyziky (paragraf 4.1.5) dosadíme za
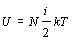 ,
,
kde i má pre molekulárny kyslík hodnotu 5.
Dostávame
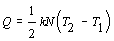 .
.
Ďalej dosadíme
za
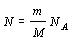
a nahradíme R = kNA ,
osamostatníme hmotnosť plynu
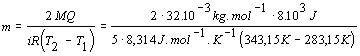
m = 0,205kg .
Za teplotu sme
dosadili T1 = (273,15 + 10
)K, T2 = (273,15 + 70 )K a
molárnu hmotnosť kyslíka nájdeme v príklade 4.2.2.1 .
Hmotnosť
kyslíka v nádobe je 0,205 kg.
