4.2.6 Entropia, druhá a tretia veta termodynamická

 

            Pre účinnosť tepelného stroja, ktorého kruhový dej medzi teplotami T₁ a T₂  (T₂ < T₁) opisuje reverzibilný Carnotov cyklus, platí

 

 .

 

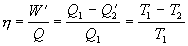Ak označíme  ,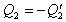

 

 potom

,

 

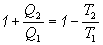alebo po matematickej úprave

 

 .

 

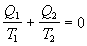Ak podiel

  

 

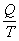
nazveme redukované teplo, vzťah môžeme vyjadriť slovami: Súčet redukovaných tepiel prijatých sústavou počas reverzibilného Carnotovho cyklu sa rovná nule.

Poslednú rovnicu môžeme zovšeobecniť aj na procesy, kedy sústava vratne prijíma teplo viac ako dvakrát

 

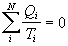,                                                                                                    ( 4.2.6.1 )

kde N je počet prijatí tepla.

 

 

Majme teraz reverzibilný kruhový dej ako na obrázku 4.2.6.1. Plochu ohraničenú do seba uzavretou krivkou  k  možno vymedziť elementárnymi Carnotovými cyklami, ako napríklad cyklus ABCD. Pri konštantnej teplote T₁ sústava prijíma teplo dQ₁ a pri konštantnej teplote T₂ prijme teplo dQ₂ .Aj pre takýto elementárny Carnotov cyklus platí rovnica 4.2.6.1. Rovnicu môžeme zovšeobecniť na všetky elementárne Carnotove cykly vytvorené na ploche ohraničenej krivkou  k ,  teda

 

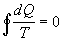 .                                                                                                     ( 4.2.6.2 )

 

V rovnici je dQ teplo vratne prijaté pri teplote T a integrácia sa vzťahuje na celý kruhový dej.

Sledujme kruhový reverzibilný dej, ktorý prebehol medzi bodmi A a B po krivkách k₁ a k₂, ako na obrázku 4.2.6.2 . Na základe platnosti rovnice 4.2.6.2, môžeme pre tento kruhový dej rozpísať nasledovne

 

 ,

 

alebo

 

 .

 

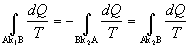Na základe posledných vzťahov môžeme usúdiť, že výsledok integrálu nezávisí od spôsobu ako sústava prešla zo základného stavu A do stavu B, ale závisí len od týchto stavov. Ak označíme

 

 ,

 

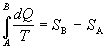potom veličinu S nazývame entropiou. Jednotkou entropie je joule na kelvin [J.K^-1]. Jej diferenciál je

 

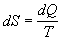 .                                                                                                     ( 4.2.6.3 )

 

Ak prebehne v sústave kruhový dej reverzibilne a sústava sa dostane do východzieho bodu, rovnicu ( 4.2.6.3 ) môžeme prepísať do tvaru

 ,

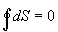ktorý je považovaný za matematickú formuláciu druhej vety termodynamickej.

Druhá veta termodynamická umožnila entropiu S definovať len ako funkciu stavu sústavy.

Pri sledovaní entropie adiabatických (dQ=0) reverzibilných dejov zapíšeme zmenu entropie nasledovne

 

 .

 

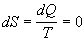Pre entropiu pri  zmene stavu sústavy z A do B potom platí

 

 .

 

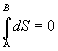Po integrácii a matematickej úprave

 

S_B - S_A = 0

 

S_A = S_B .

 

Posledý vzťah môžeme slovami vyjadriť: Počas adiabatických reverzibilných dejov sa entropia sústavy nemení.

Gibbs tieto vratné adiabatické deje nazval izentropické deje.

Vo viacerých učebniciach fyziky by sme našli matematické postupy ktoré dokazujú,  že účinnosť tepelných strojov založených na reverzibilnom Carnotovom cykle je najvyššia. Teda účinnosť tepelných strojov založených na ireverzibilnom deji je vždy menšia. Preto platí

 

 .

 

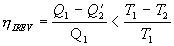Ak označíme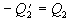  

 

a rovnicu upravíme, dostávame tvar

 

 

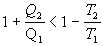
a po úprave

 

 .

 

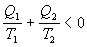Poslednú rovnicu môžeme zovšeobecniť aj na proces, kedy sústava prijíma teplo viackrát

 

,

 

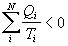kde N je počet prijatí tepla. A pre ireverzibilný kruhový dej prebiehajúci spojite platí

 

 .

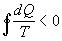Majme teraz ireverzibilný kruhový dej prebiehajúci medzi bodmi A a B ako na obrázku 4.2.6.3. Dej prebieha z bodu B do bodu A po krivke  k₁  reverzibilne a z bodu A do B po krivke  k₂  ireverzibilne. Pre tento dej platí

 

 .

 

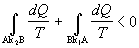Po úprave integračných hraníc môžeme napísať

 

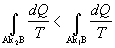 .                                                                                       ( 4.2.6.4 )

 

Z predchádzajúcich poznatkov o narastaní entropie pre reverzibilné deje platí

 

 

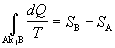
a s použitím vzťahu 4.2.6.4 prechádza posledná rovnica do tvaru

 

 .

 

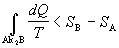Pri sledovaní entropie adiabatických (dQ = 0) ireverzibilných dejov potom môžeme písať

 

,

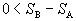alebo

.

 

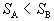Posledný vzťah môžeme slovami vyjadriť nasledovne: Pri všetkých ireverzibilných dejoch prebiehajúcich v sústavách od okolia tepelne izolovaných sa entropia sústavy zväčšuje.

 

            Sústavou pokusov pri teplotách T® 0 sa zistilo, že niektoré vlastnosti látok ( elektrický odpor vodičov, teplotná rozťažnosť, molárna tepelná kapacita) nie sú závislé od teploty. Alebo opačne - zmenou žiadnych vonkajších parametrov látky pri teplote T® 0 nemožno dosiahnuť zníženie teploty na T = 0 . Túto skutočnosť Planck vyjadril vetou:

Čistú tuhú látku nie je možné konečným procesom ochladiť na nulovú Kelvinovu teplotu.

Je pravdepodobné, že v blízkosti teploty T = 0 prestáva tepelný pohyb častíc, čiže aj už existujúce nerovnovážne stavy v sústave môžu existovať ľubovolne dlho. Tieto poznatky zovšeobecnil Nernst v tretej vete termodynamickej. Jej znenie je:

Pre ľubovoľný izotermický dej prebiehajúci pri teplote T® 0 je zmena entropie nulová. Vetu doplnil Planck tým, že položil entropiu pri teplote T® 0 rovnú nule S_(T=0) = 0. Tým odstránil neurčitosť v určení absolútnej hodnoty entropie každého stavu látky.

 

 

Príklad 4.2.6.1

 

Aká je zmena entropie 1 kg vodnej pary zohriatej na 100 ⁰C vzhľadom na stav v kvapalnom skupenstve pri teplote 20 ⁰C ? Hmotnostná tepelná kapacita vody je  c_v = 4186 J.kg^-1. K^-1  a skupenské teplo vyparovania vody  l_v = 2,256.10⁶ J.kg^-1.

 

Riešenie :

Sledovanú zmenu entropie môžeme rozdeliť na dve časti. Zmena entropie m = 1kg vody pri jej zohriatí z teploty t_A  = 20 ⁰C Þ T_A = 293,15 K na bod varu t_B  = 100 ⁰C Þ T_B = 373,15 K a zmenu entropie vody počas jej premeny na paru pri konštantnej teplote t_B . Celkovú zmenu entropie zapíšeme

 

.

 

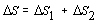Pre výpočet jednotlivých zmien entropie použijeme vzťah 4.2.6.3 a dosadíme

 

 .

 

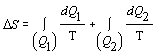Proces zohrievania vody z teploty T_A na T_B opíšeme rovnicou dQ₁ = mc_V dT  a vyparenie vody rovnicou  dQ₂ = l_V dm. Pritom nesmieme zabudnúť, že vyparovanie sa deje pri konštantnej teplote T_B. Za týchto podmienok zmenu entropie vypočítame

 

 

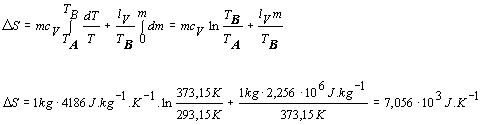
Zmena entropie vodnej pary je 7,056.10³ J.K ^-1 .