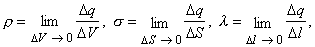6.1.1.7 Spojité rozloženie nábojov - hustota náboja

Silové pôsobenie medzi nabitými telesami možno presne experimentálne určiť iba v najjednoduchších prípadoch - vzájomné pôsobenie dvoch bodových nábojov a pod. Experimentálne meranie rozloženia nábojov v nejakom telese je prakticky len veľmi ťažko realizovateľné. Preto pri zložitejších sústavách nábojov musíme vytvoriť model rozloženia nábojov v telese a až na základe teoretického výpočtu pôsobiacich síl overovať platnosť a primeranosť tohoto modelu. Často sa stretávame s tým, že máme veľmi veľký počet bodových nábojov, ktoré sa nachádzajú v malom objeme, pričom na makroskopickej úrovni je bodový charakter jednotlivých nábojov už nepodstatný, ale dominuje veľké množstvo náboja v každom malom objeme. Vtedy môžeme náboje chápať akoby boli spojito rozložené v priestore a pre takéto sústavy zaviesť pojem "spojitého rozloženia elektrických nábojov" v určitej oblasti.

Predstavme si kocku s hranou a, v ktorej sú rovnomerne rozložené bodové náboje. Celkový náboj kocky je q,  jej objem je V = a³ . Ak si predstavíme vo vnútri menšiu kocku o hrane b < a, tak v nej bude náboj q₁, pričom jej objem je V₁ . Ak sú náboje rozložené skutočne rovnomerne, tak určite bude platiť

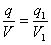                                                                                                                         (6.1.2)

bez ohľadu na rozmery menšej kocky. Preto podiel náboja a objemu kocky môžeme považovať za istú charakteristiku rozloženia nábojov. Na základe analógie s hustotou látok pre túto charakteristiku zavedieme pojem "objemová hustota elektrického náboja" a budeme ju obvykle označovať gréckym písmenom r . Malý objem, v ktorom spočítavame náboje  nemusí byť práve kocka, môže to byť iný geometrický útvar napr. dodekaeder, ale výpočty sú zrejme najjednoduchšie pre kocku.

Ak je elektrický náboj v nejakej oblasti priestoru rozložený nerovnomerne, tak podiel náboja a objemu, v ktorom sa tento náboj nachádza zrejme závisí od veľkosti objemu, ktorý sme si zvolili. Ak však budeme objem V voliť dostatočne malý, tak tento podiel už bude konštantný a pre takúto malú oblasť bude r predstavovať lokálnu objemovú hustotu elektrického náboja.

V elektrostatike sa však stretávame aj s tým, že náboje sú rozložené iba na povrchu telies. Vtedy má význam zaviesť "plošnú hustotu elektrického náboja" definovanú ako

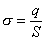                                                                                                                    (6.1.3)

kde S je plocha na ktorej spočítavame náboj.

Niekedy má uvažovaná plocha jeden rozmer podstatne väčší ako sú ostatné rozmery. Napríklad dlhý tenký valec s nábojom na povrchu. Z väčšej vzdialenosti sa nám takýto valec bude javiť ako tenké dlhé nabité vlákno, kde podstatné rozmery súvisia iba s jeho dĺžkou. V takom prípade zavádzame "dĺžkovú hustotu elektrického náboja" definovanú ako

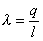                                                                                                                     (6.1.4)

kde q je náboj pripadajúci na úsek vlákna dĺžky l .

Poznámka: Exaktný matematicky postup by si vyžadoval zaviesť jednotlivé hustoty elektrického náboja ako limity podielov