6.1.3.3 Princíp superpozície

Skúmajme teraz, aké bude silové pôsobenie na náboj q v bode r  od väčšieho počtu bodových nábojov q₁, q₂, … , q_n, ktoré sa nachádzajú v bodoch r₁, r₂, …, r_n. Sila pôsobiaca na tento náboj pochádzajúca od náboja q_i je 

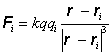                                                                                                              (6.1.9)

Experimenty ukazujú, že výslednú silu dostaneme ako vektorový súčet takýchto síl od všetkých pôsobiacich nábojov. Teda

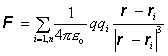                                                                                            (6.1.10)

Vzťah (6.1.10) vyjadruje "princíp superpozície elektrických síl".

___________________________________________________________________________

Príklad 6.1.3.3. Tri náboje -q sú umiestnené vo vrcholoch rovnostranného trojuholníka s dĺžkami
strán a. Náboj Q je v jeho ťažisku.
a) Odvoďte výraz pre silu, ktorá pôsobí na jeden z nábojov -q. Určite smer tejto sily.

b) Aký musí byť vzťah medzi hodnotami nábojov ,aby sila pôsobiaca na náboj -q bola nulová? Je tento systém elektrických nábojov stabilný?

Riešenie:

a) Na náboj –q v mieste 1 pôsobia náboje z miesta 2, 3 silami F_21,  F₃₁ a náboj Q silou F₄.
Výsledná sila F_v , ktorou tieto náboje pôsobia na náboj v mieste 1, je daná vektorovým súčtom 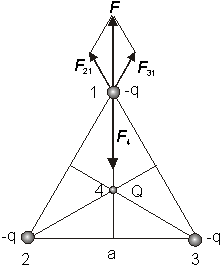.Možno  písať

F_v = F₄.+ F₂₁ + F₃₁

Podľa Coulombovho zákona veľkosť sily F_21, F₃₁ je

F₂₁ = F_{31 =}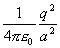 

Veľkosť sily F podľa obrázka je         F = .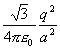

Veľkosť sily F₄     je   

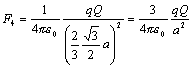
Pre veľkosť výslednej sily môžeme písať F_v =F- F₄ .

b) Náboj Q umiestnený v ťažisku trojuholníka má opačný náboj, teda kladný .

Výsledná sila F_v  je nulová, preto  F = F_4.

Dosadením  dostaneme

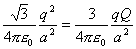    z toho

 vzťah medzi nábojmi q, Q je  
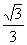Q = q .  

Tento systém nábojov je labilný. Stačí, aby sa jeden z nábojov máličko vychýlil zo svojej polohy, a nastane pohyb nábojov, čím sa celý systém rozpadne. Vo všeobecnosti sa ukazuje, že nie je možné vytvoriť stabilnú rovnovážnu konfiguráciu nábojov, ktoré sú v pokoji.

___________________________________________________________________________