Matematicky
môžeme Coulombov zákon formulovať nasledovne:
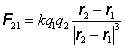 , (6.1.6)
, (6.1.6)
kde F21 je sila pôsobiaca na náboj q2 pochádzajúca od náboja q1 a r2 , r1 sú polohové vektory týchto nábojov. Pritom
budeme vždy dodržiavať konvenciu, že prvý index určuje objekt, na ktorý sila pôsobí
a druhý index je spojený s pôvodom tejto sily. Správne by sme mali indexy oddeľovať
čiarkou, teda písať F2,1 avšak obyčajne, pokiaľ nie sú indexy vyššie ako číslica 9 a ich
interpretácia je jednoznačná, tak sa používa zjednodušené označovanie bez
oddeľujúcej čiarky.
|
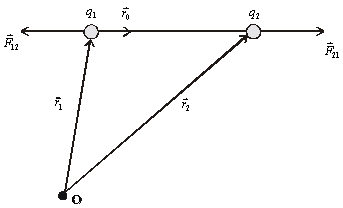
Obr.
6.1.3.2
Silové
pôsobenie medzi dvoma nábojmi
|
Rovnica (6.1.6) rešpektuje vektorový charakter
pôsobiacej sily a súčasne aj príťažlivý a odpudivý charakter sily v závislosti
od výsledného znamienka súčinu nábojov. V menovateli formálne vystupuje tretia
mocnina vzájomnej vzdialenosti nábojov, ale treba si uvedomiť, že výraz
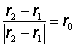
vyjadruje jednotkový vektor v
smere pôsobiacej sily.
Konštanta
úmernosti k vo vzťahu (6.1.6) závisí
od použitej sústavy jednotiek. V SI sústave platí:
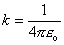 (6.1.7)
(6.1.7)
kde eo = 8,854 . 10-12 A2kg-1m-3s4
. Veličinu e0 nazývame permitivitou vákua
(niekedy sa nazýva tiež elektrická konštanta). Faktor 4p v
menovateli je zavedený preto, aby nevystupoval v iných vzťahoch, ktoré vyplývajú
z Coulombovho zákona. Tieto potom vyzerajú jednoduchšie a elegantnejšie.
Treba
pripomenúť, že sily, ktoré vystupujú v Coulombovom zákone sú sily akcie
a reakcie. Teda platí
F21 = - F12 (6.1.8)
Slovami
môžeme Coulombov zákon formulovať nasledovne: Dva bodové náboje, ktoré sú v pokoji, pôsobia na seba silou,
ktorá je priamo úmerná súčinu veľkostí nábojov a nepriamo úmerná druhej
mocnine ich vzájomnej vzdialenosti.
_________________________________________________________________________________________________________________________
Príklad 6.1.3.1 Dve uhlíkové guľôčky , z
ktorých každá má hmotnosť 1 g a je nabitá záporným nábojom , sú zavesené v
jednom bode na nitiach dlhých 10 cm. Silové pôsobenie má za následok, že sa
nite rozostúpia o 60o uhol.
b) Koľko elektrónov bolo prinesených na každú guľôčku
pri nabíjaní?
c) Akou gravitačnou silou na seba guľôčky pôsobia?
|
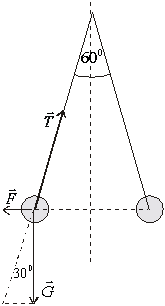
Obr.6.1.3.3
|
Riešenie:
a) Súčet elektrostatickej odpudivej sily F, sily T ktorou niť
pôsobí na guľôčku a tiaže guľôčky G sa
musí rovnať 0.
tg 300
= F/ m.g
F = m.g. tg 300 =5,66.10-3 N
b) Z Coulombovho zákona dostaneme pre veľkosť náboja
q = 2r.(p.eo .F)1/2
z obrázku plynie
r = 2.l.sin 300 =0.1 m
potom q = 7.93.10-8 C
Počet elektrónov privedených na guľôčku je q/e =
7,93.10-8 C / 1,6.10-19 C = 4,896 .1011
c)Pre gravitačnú silu, ktorou na seba pôsobia 2
guľôčky s hmotnosťami 1g dostaneme
F = 6,67.10-11 . 10-6 /10-2 N = 6,67 .10-15 N
Vidíme, že elektrostatická odpudivá sila medzi
guľôčkami je 8,5.1011 krát väčšia ako gravitačná príťažlivá sila ,
preto gravitačnú príťažlivú silu môžeme zanedbať.
_________________________________________________________________________________
Príklad
6.1.3.2
Vypočítajte klasickú obežnú rýchlosť elektrónu ,obiehajúceho okolo jadra atómu vodíka. Hmotnosť elektrónu je 9,1.10-31
kg. Polomer kruhovej dráhy elektrónu v atóme vodíka je podľa Bohra 0,52 .10-10 m.
Riešenie :
Dostredivá sila sa rovná Coulombovej sile
 .
.
Elektrostatickú silu počítame z Coulombovho
zákona
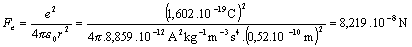 ,
,
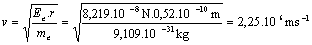
Rýchlosť elektrónu na obežnej dráhe je 2,25.106 m.s-1
____________________________________________________________________________________________________________________________