13.2.2    Atóm vodíka 

 

Atóm vodíka je najjednoduchší atóm, skladajúci sa z jedného elektrónu a jedného protónu, viazanými elektrostatickou interakciou. Z  experimentov  bolo  známe, že atóm  nežiari, ak sa nachádza v základnom  stave, t.j. v stave s najnižšou energiou. Ak  však zvýšime jeho vnútornú energiu, atóm sa dostane do excitovaného stavu, t.j. do stavu s energiou nad základným stavom. Atóm  v excitovanom stave vysiela žiarenie.

 

13.2.2.1 Bohrov model atómu

Na sklonku devätnásteho storočia bolo zistené, že spektrum  atómov môže byť tvorené radom diskrétnych hodnôt frekvencií, vtedy hovoríme o čiarovom spektre. Najjednoduchšie spektrum odpovedá atómu vodíka.  Spektrálne čiary v atómových spektrách nie sú rozložené náhodile, ale   sa radia  do istých skupín, nazývaných spektrálne série. Vlnové dĺžky prislúchajúce jednotlivým  pozorovaným čiaram v každej sérii, možno určiť jednoduchým empirickým vzorcom, pričom je nápadná podobnosť medzi jednotlivými vzorcami pre rôzne série,  ktoré obsahujú úplné spektrum uvažovaného prvku.

 

 

 

 

 

Prvá takáto séria,  objavená vo viditeľnej časti spektra atómu vodíka a pozostávajúca  zo štyroch čiar (obr. 13.2.2.1),  sa nazýva Balmerova séria, podľa švajčiarskeho vedca, ktorý v roku 1885  vyjadril  vlnové dĺžky tejto série  vzorcom

 

                                                                 (13.2.2.1)

 

kde C je určitá konštanta  a  s  = 3, 4, ... . Neskoršie  Rydberg zistil, že Balmerov vzorec možno upraviť, po zavedení  vlnočtun =1/l ,  na  tvar

 

 

                                   (13.2.2.2)

 

kde   R  je   Rydbergova    konštanta  (resp.  vlnočet  )  pre  vodík,  ktorej    hodnota je

R  = 10 973 730  m-1 .                                                                                    (13.2.2.3)

                                                                                                                     

 

Postupne boli v spektre vodíka zistené i ďalšie  série a to  v infračervenej i v ultrafialovej oblasti spektra (obr. 13.2.2.2).

 

 

 

 

Vysvetliť pozorované čiarové spektrá atómu vodíka sa podarilo dánskemu fyzikovi Nielsovi Bohrovi (1885-1962), na základe  poznatkov týkajúcich  matematického vyjadrenia vlnočtov spektrálnych sérií [Balmerov (13.2.2.1) resp. Rydbergov vzorec (13.2.2.2)], poznatkov Planckovej teórie žiarenia zahriatych  telies  a Einsteinovej teórie fotoefektu. 

Teóriu atómu vodíka zhrnul do troch postulátov:

·        1. Bohrov postulát stacionárnych stavov

Atómy môžu existovať v istých stacionárnych stavoch, v ktorých nevyžarujú energiu. Tieto stacionárne stavy korešpondujú „orbitám“ v klasickej predstave pohybujúcich sa elektrónov okolo jadra,   obdobne ako predpokladal planetárny model atómu. Elektróny na týchto orbitách neemitujú  elektromagnetické žiarenie i napriek tomu, že konajú pohyb so zrýchlením.

 

·        2. Bohrov postulát kvantovania orbitálnych dráh

Celkový orbitálny moment hybnosti elektrónu ln  nachádzajúceho sa na stacionárnej orbite sa  rovná celočíselnému násobku Planckovej konštanty h, resp. redukovanej Planckovej konštanty ħ = h/2p   ( nazvanej hatrans).

 

                                                               (13.2.2.4 )

 

kde rn je polomer n-tej kruhovej dráhy (orbity) a  n  je prirodzené číslo. 

 

·        3. Bohrov postulát frekvenčnej podmienky

Atóm emituje kvantum elektromagnetického žiarenia (fotón), keď elektrón preskočí z kvantovej dráhy s kvantovým číslom  m na kvantovú dráhu s menším číslom n . Energia fotónu je určená rozdielom energií na kvantovej dráhe pred  a po vyžiarení:

 

E = hf = Em - En .                                                                                          (13.2.2.5)                              

 

Bohrove postuláty nemožno odvodiť z klasickej fyziky. Možno ich vysvetliť len na základe kvantovej mechaniky. Bohrov model určuje:

1/ vzťah pre energiu  elektrónu na stacionárnej dráhe v atóme vodíka

 

 

                                                              (13.2.2.6)

 

kde e0  je permitivita vákua, me  hmotnosť elektrónu, Z je protónové číslo a n hlavné kvantové číslo.  (Pre atóm vodíka platí  Z = 1.)

 

Pre základný stav (n =1) možno určiť energiu základného stavu E1, ktorá má hodnotu E1= – 13,6 eV.    

 

Poznámka: Rovnica (13.2.2.6 -13.2.2.8) platí aj pre atómu vodíka podobné atómy, t.j. ionizované atómy, ktoré majú 1 valenčný elektrón, ako napr.  Li+...

 

2/ polomer n-tej kruhovej dráhy

 

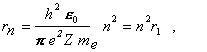                                                                   (13.2.2.7)

 

 

odvodený z podmienky, že dostredivá sila je spôsobená coulombickým priťahovaním elektrónu k jadru: t.j. platí ½fd½ = ½fc½

 

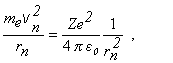                                                                           (13.2.2.8)

                                                                                                                     

 

 s využitím kvantovej podmienky vzťah (13.2.2.4).

 

Polomer orbity s hlavným kvantovým číslom n = 1 sa nazýva Bohrov polomer,  r1 = 0,529177249 .10-10 m.

3/ frekvencie v čiarovom spektre vodíka

 

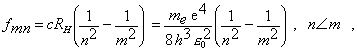                             (13.2.2.9)

 

kde c je rýchlosť svetla , RH  Rydbergova konštanta pre H-atóm a  n, m sú prirodzené čísla.

 

RH = 1,0967758.107 m-1. Ak m =µ   dostávame hranu série pre dané n.

 

Potvrdenie správnosti Bohrovho modelu :

 

·        pomerne dobrý súhlas hodnoty  Rydbergovej  konštanty RH,  určenej zo spektier a vypočítanej z Bohrovho modelu R¥. Nepatrný rozdiel vyplýva z predpokladu nehybného jadra (t.j. nekonečne ťažkého jadra).  Ak zvážime, že protón má konečnú hmotnosť, je nutné do vzťahu miesto hmotnosti elektrónu me  dosadiť redukovanú hmotnosť mred , definovanú vzťahom

 

 

 

·        Franckov a Hertzov pokus, uskutočnený v roku 1913, ktorý experimentálne dokázal existenciu diskrétnych energetických hladín urýchľovaním elektrónov atómov ortuti  vo vákuovej trubici.

 

 

––––––––––––––––––––––––––––––––-

Príklad  13.2.2.1 Na základe Bohrovej teórie atómu vodíka  odvoďte vzťah  pre polomer dráhy, rýchlosť na n-tej kvantovej dráhe v atóme vodíka. Určite hodnoty uvedených   veličín  pre  tretiu  kvantovú dráhu.

Riešenie:  Na základe Bohrovej teórie sa elektrón pohybuje po dovolených kruhových orbitách okolo jadra pod vplyvom Coulombovej príťažlivej sily medzi elektrónom a kladne nabitým jadrom. Podmienkou pre stabilitu pohybu je rovnosť veľkosti sily  dostredivej a elektrostatickej , t.j. platí  rovnica (13.2.2.8)

 

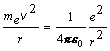                                                                                                             (1)

 

Dovolené   orbity  sú   určené  kvantovou   podmienkou  (13.2.2.4)    mv rn  = n h/2p . Ak si z uvedených rovníc vyjadríme kvadrát rýchlosti,  resp. rýchlosť,  dostaneme nasledovné rovnice

 

  ,                                                                                                          (2)

 

 

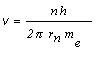    .                                                                                                           (3)

 

 Umocnením rovnice (3)  na druhú a porovnaním obidvoch pravých strán rovníc (2) a (3) dostávame vzťah  (13.2.2.7) pre polomer dráhy

 

 

 

  .                                                                                                (4)

 

 

 

V prípade n = 3   pre  číselnú hodnotu polomeru tretej orbity  dostaneme    rn = 47,619.10-11  m.  Obvodovú rýchlosť elektrónu na n-tej dráhe určíme z kvantovej podmienky  (13.2.2.4)

 

 ,                                                                                                              (5)

 

po dosadení  za polomer z rovnice (4)  a následných úpravách  dostávame

 

 
                                                               

a dosadení číselných hodnôt určíme obvodovú rýchlosť elektrónu na tretej sfére

 

v 3 = 7,2.105 m. s-1.

––––––––––––––––––––––

 

 Príklad  13.2.2.2  Vypočítajte frekvenciu žiarenia potrebného na excitáciu elektrónu vo vodíkovom atóme zo základného stavu do najbližšieho excitovaného stavu.

Riešenie: Druhý Bohrov postulát ukazuje, že ak elektrón preskočí z jednej dovolenej orbity s hlavným kvantovým číslom nm na druhú orbitu s hlavným kvantovým číslom nn , (m > n) emituje fotón frekvencie fmn určenej  vzťahom (13.2.2.9)

 


 


resp.  fotón s  vlnovou dĺžkou l určenou rovnicou

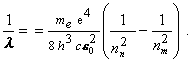
Keďže  chceme dosiahnuť prechod z prvého excitovaného stavu nm  =2 do základného stavu s  nn =1 musíme atóm ožiariť s frekvenciou f

 


 

 


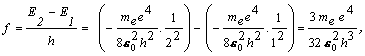
resp. jednoduchšie ak uvážime, že E1   = -13,6  eV  a  E2 = E1/4 ,  pre f dostaneme

 

f =( E2   - E1)/h = 3(13.6 eV)/4h =2,466.1015 Hz .

 

–––––––––––––––––––––––––

Príklad  13.2.2.3 Vypočítajte frekvenciu žiarenia potrebného na  ionizáciu atómu vodíka v základnom stave. Akú „farbu“ budú mať tieto fotóny? Porovnajte ich s „farbou“ žiarenia potrebného na excitáciu do prvej vzbudenej hladiny. (Pozri príklad 13.2.2.2).

Riešenie: Aby došlo k ionizácií atómu vodíka, musíme elektrónu dodať energiu, ktorá sa rovná½E1½, t.j. 13,6 eV  Vtedy sa elektrón uvoľní z atómu. Frekvenciu žiarenia, spôsobujúceho ionizáciu atómu vodíka určuje vzťah  (13.2.2.9) , kde sme dosadili  n n= 1 a nm  =µ

 

 

 

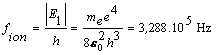
„Farba“ fotónom je priradená iba vo viditeľnej oblasti elektromagnetického spektra. Zistíme odpovedajúce vlnové dĺžky  žiarenia, spôsobujúce ionizáciu i emisiu z prvej excitovanej hladiny na základnú. Prepočítaním cez rýchlosť svetla dostaneme vlnové dĺžky a to

 

 ,    

 

    

„Farbu “ fotónom nemôžeme priradiť,  keďže v obidvoch prípadoch vlnové dĺžky spadajú do ultrafialovej oblasti.

 

 

Príklad  13.2.2.4 Na základe Bohrovho modelu atómu  odvoďte vzťah  pre celkovú energiu elektrónu v atóme vodíka nachádzajúceho sa  na kruhovej dráhy s hlavným kvantovým číslom n.

Riešenie: Celkovú energiu si vyjadríme ako súčet kinetickej a potenciálnej energie elektrónu na orbite s hlavným kvantovým číslom  n.

 

En =  Ekn +Epn  .

 

Ekn  určíme na základe vzťahu (2) z príkladu 13.2.2.1. Pre potenciálnu energiu v poli jadra s nábojom Ze v mieste s   rn dostávame

 

 

 

 

Po dosadení vzťahu (4) z príkladu 13.2.2.1 za polomer rn,  dostaneme pre celkovú energiu

 

–––––––––––––––––––––––––––––––––––-

 

Kontrolné otázky

 

1.      Dokážte súvislosť medzi Rydbergovou konštantou vystupujúcou v Rydbergovej rovnici  (13.2.2.2) a konštantou, nachádzajúcou sa vo vzťahu pre diskrétne hodnoty energie  (13.2.2.6)  atómu vodíka.

2.      Definujte pojem „redukovaná hmotnosť“.

3.      Zmenia sa energetické hladiny atómu vodíka,  ak pohyb jadra nezanedbávame? Ak áno, ako?

4.      Napíšte vzťah pre vlnové dĺžky prechodov v Lymannovej sérii.

5.      Aké série boli pozorované v infračervenej oblasti spektra?

6.      Vo viditeľnej časti spektra atómu vodíka boli pozorované  spektrálne čiary. Ich vlnovú dĺžku možno určiť na základe matematického vzťahu. Napíšte tento vzťah a meno objaviteľa tejto série.

7.      Definujte pojem hrana série.

8.      Definujte pojem  základný stav atómu.

9.      Vysvetlite pojem „excitovaný stav atómu“.

10.   Aká energia,  vyjadrená v eV, prináleží základnému stavu atómu vodíka?

11.  Vyjadrite energiu elektrónu v  atóme vodíka ako funkciu hlavného kvantového čísla a energie základného stavu.

12.  Vyjadrite periódu obehu elektrónu v atóme vodíka, ako funkciu hlavného kvantového čísla.

13.  Vyjadrite potenciálnu a kinetickú energiu elektrónu na  orbite s hlavným kvantovým číslom n ako  funkciu polomeru tejto dráhy, resp. ako  funkciu hlavného kvantového čísla.

14.  V akom vzťahu je Planckova konštanta k redukovanej Planckovej konštante (hatrans)?

15.  Vysvetlite pojem Bohrov polomer a určite jeho veľkosť.

16.  Napíšte vzťah určujúci polomer n-tej dráhy ako funkciu Bohrovho polomeru a hlavného kvantového čísla.

17.     Zistite, či sa prekrývajú niektoré z prvých šiestich  energetických hladín elektrónu v atóme ionizovaného hélia He+ s energetickými hladinami elektrónu v atóme vodíka.