6.3.4 Vektor polarizácie

Pri atómovej polarizácii nastáva posunutie všetkých kladných nábojov v smere poľa za súčasného posunutia záporných nábojov proti smeru poľa. Podobné je to aj pri polarizácii iónovej a polarizačnej. Zmeny spôsobené v dielektriku vplyvom polarizácie sa dajú pri všetkých typoch polarizácie popísať formálne rovnakým spôsobom. Kladné náboje rozložené v celom priestore dielektrika sa posunú o dĺžku l vzhľadom na náboje záporné (Obr. 6.3. 1). Pole, v ktorom sa malý objem dielektrika ohraničený vzdialenosťou l a plôškou dS nachádza, môžeme považovať za homogénne. Potom aj rozloženie kladného a záporného náboja na plôškach dS má konštantnú plošnú hustotu  resp. 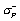 a pole vzniknuté v takejto elementárnej bunke vplyvom polarizácie je homogénne, také isté ako pole medzi dvoma nekonečne veľkými rovinami nabitými nábojmi opačného znamienka s plošnými hustotami 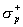 resp. 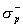. Intenzita takéhoto poľa je podľa (6.2.6)

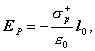                                                                                                          (6.3.4)
kde l₀ je jednotkový vektor polohového vektora l kladného náboja vzhľadom na náboj záporný v takejto bunke. Elektrický moment jedného dipólu v tejto bunke je

      

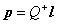
a elektrický moment celej bunky je

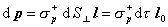                                                                                               (6.3.5)
kde 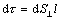 je objem elementárnej bunky. Objemová hustota elektrického momentu v polarizovanom dielektriku sa nazýva elektrická  polarizácia (vektor elektrickej polarizácie)

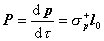      .                                                                                                 (6.3.6)
Je to elektrický moment pripadajúci na jednotku objemu dielektrika a jeho veľkosť sa rovná hustote 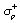 kladného náboja „vylúčeného“ polarizáciou na hladine bunky. Táto hustota sa nazýva hustota polarizačného náboja. Predpokladajme, že dielektrikum je lineárne, to znamená, že relatívny posun l nábojov v smere poľa je úmerný intenzite poľa. Je to vtedy, ak sily elektrického poľa sú malé oproti väzbovým silám molekúl.

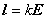      .                                                                                                               (6.3.7)
Potom

      .
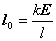Po dosadení do (6.3.4)

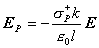      .       (6.3.8)
Konštanta

             (6.3.9)
popisujúca vlastnosti dielektrika sa nazýva elektrická susceptibilita. Potom intenzita E_p elektrostatického poľa vytvoreného vplyvom polarizácie je

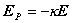                                                                                                         (6.3.10)
a vektor elektrickej polarizácie

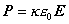      .                                                                                                   (6.3.11)
Hustota  polarizačného náboja  vyplýva zo vzťahov  (6.3.7,9).

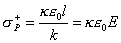      .                                                                                      (6.3.12)
E vo vzťahoch (6.3.10,11,12) je intenzita skutočného poľa, ktoré existuje v dielektriku, to znamená poľa  voľných nábojov a poľa vzniknutého vplyvom polarizácie dielektrika. Polarizácia závisí totiž od skutočného poľa a nielen od poľa, ktoré by v danom mieste bolo, keby sa dielektrikum nepolarizovalo. Ak označíme 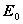 intenzitu poľa, ktoré má pôvod len vo voľných nábojoch okolitých nabitých telies, intenzita skutočného poľa bude

                                                                                           (6.3.13)
z toho

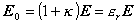                                                                                         (6.3.14)
kde konštanta

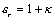                                                                                                             (6.3.15)
sa nazýva relatívna permitivita  prostredia.

Polarizáciou elementárnej bunky dielektrika vzniknú na jej protiľahlých hladinách vrstvy opačných nábojov s plošnou hustotou 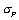, úmernou intenzite poľa. Tieto dve vrstvy nábojov vytvárajú dodatočné pole s intenzitou E_p opačne orientovanou ako intenzita E₀  pôvodného vonkajšieho poľa. Vonkajšie pole sa vplyvom polarizácie bude v bunke zoslabovať. Rovnako sa chová dielektrikum aj v susednej elementárnej bunke, pričom ako bolo ukázané v odseku (6.1.9.1) pre dve opačne nabité plochy, pole mimo takejto bunky je nulové a teda bunky si polia nebudú navzájom ovplyvňovať. Z uvedeného vyplýva, že odvodené výsledky sa dajú zovšeobecniť na ľubovoľný objem.