3.1.2         Hydrostatický tlak

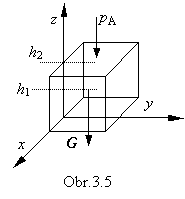
Majme kvapalinu hustoty r v nádobe podľa obr. 3.5. Jediná objemová sila je gravitačná sila. Je orientovaná v zápornom smere osi z. Zložky intenzity tejto sily sú  E_x  = E_y  = 0,   E_z = – g.  Po dosadení do rovníc ( 3.4 a-c), za použitia vzťahu

 f = r E,  dostávame:

 

 

 

 

 

 

 

 

 

 ;             ;       a      

 

Vynásobme tieto rovnice postupne dx, dy, dz a sčítajme ich. Dostávame:

 

 ,                                                                                                       (3.9)

 

kde  

 

 

je úplný diferenciál tlaku.

 

V rovnici (3.9 ) môžeme separovať premenné a integrovať ju:                              

 

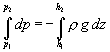                                                                                                      (3.10)

 

Po integrácii potom:

 

.

 

Nech tlak na hladine je vonkajší atmosférický tlak p₂ = p_A  a (h₂ - h₁) = h je výška kvapaliny nad daným miestom. Potom pre celkový tlak vo vnútri kvapaliny dostávame:

 

.                                                                                                            (3.11)

 

Člen r g h  predstavuje hydrostatický tlak. Je to tlak, ktorý v dôsledku tiažovej sily vytvára stĺpec kvapaliny výšky h.

Tento istý výsledok získame veľmi ľahko z rovnice (3.8). Platí  r j + p  = konšt., potenciál homogénneho gravitačného poľa j  = g h, a teda  r g h₁ + p₁ = rgh₂ + p₂.

Ak označíme p₁ = p,  h₂ – h₁ = h  a p₂ = p_A  dostávame  p = p_A + rgh.

––––––––––––––––––––––––––––––––––––––

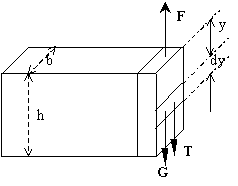
Príklad 3.4  Aká sila je potrebná na zdvihnutie priehradky (obr.3.6), ktorá je pod tlakom vody? Hmotnosť priehradky je m = 200 kg, jej šírka b = 4 m, hĺbka vody  h = 2 m a faktor trenia priehradky o opory je m  = 0,3.

 

Riešenie:

Pohybová rovnica má tvar:   m a = F + G + T ,

kde  F = F j   je hľadaná sila, G = mg (–j)  je tiažová sila, T = m  F_p (–j)  je sila trenia, ktorá je úmerná tlakovej sile F_p vody na priehradku. Pri rovnomernom pohybe musí platiť:   0 = F – mg - m F_p

Tlak pôsobiaci na priehradku závisí od hĺbky  y  podľa vzťahu:  p = p_A+ r g y.

Vyjadrime najprv tlak na elementárnu plôšku   dS = b dy ,

teda na body nachádzajúce sa v rovnakej hĺbke  y  pod hladinou: p = p_A+r g y – p_A

(atmosférický tlak pôsobí na stenu z obidvoch strán).

 

 

Obr. 3.6

 

Pre tlakovú silu na túto plôšku dostaneme:                                                                    

 

dF_p = p dS = r g y b dy .                      

 

 

Integráciou dostaneme celkovú tlakovú silu na bočnú stenu:

 

.

 

Celková sila potrebná na zodvihnutie priehradky bude:

 

 

 

Pri dvíhaní sa bude táto sila z tejto maximálnej hodnoty postupne zmenšovať, pretože sa bude zmenšovať tlaková sila.

––––––––––––––––––––––––––––––––––––––––