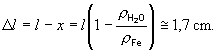3.1.4    Archimedova sila

Dôsledkom hydrostatického tlaku je Archimedova vztlaková sila. Majme v kvapaline hustoty r úplne ponorené teleso rozmerov dx, dy, dz (obr.3.7).

                

 

 

 

 

 

 

 

 

 

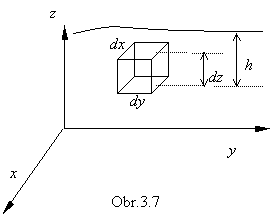
Hydrostatický tlak je iba funkciou súradnice z, v dôsledku čoho sa rušia zložky tlakových síl pôsobiacich na element dV v smere osí x a y. Zložka tlakových síl v smere osi z sa rovná rozdielu tlakových síl pôsobiacich na dolnú a hornú základňu:

 

dF_z = r g h dx dy – r g (h – dz ) dx dy = r g dV.

 

Na teleso objemu dV bude pôsobiť smerom nahor sila, ktorej veľkosť sa rovná tiaži kvapaliny telesom vytlačenej. 

 

Archimedov zákon: Teleso je nadľahčované silou, ktorá sa rovná tiaži telesom vytlačenej kvapaliny.

 

 

Príklad 3.6 Zistite, či koruna s hmotnosťou 1,47 kg, ktorá keď je celá ponorená do vody váži v nej 1,34 kg, je zhotovená zo zlata.

 

Riešenie: Hustota koruny s hmotnosťou  m_k a objemom V_k  je

 

 .

 

Ak ju úplne ponoríme do vody, bude na ňu pôsobiť výsledná sila (zdanlivá tiaž) vo vode:  F = G – F_v , kde  G = m_k g  je tiažová sila na vzduchu, vztlaková sila

 

 - je objem vytlačenej vody.

 

Ak je teleso úplne ponorené, platí  V_H2O = V_k .

 

Potom:

 

Odtiaľ pre hustotu koruny dostaneme:

 

 

 

 

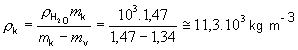
Keďže  r_Au = 19,3.10³ kg m^-3 , koruna nie je vyrobená zo zlata, ale podľa tabuliek je olovená.

 

 

Príklad 3.7  V mori pláva ľadová kryha. Vypočítajte celkový objem kryhy, keď nad vodu vyčnievajúca časť kryhy má objem

V₁  = 180 m³.

 

Riešenie:

Celkový objem kryhy je   V = V₁ + V₂   kde  V₂  je objem ponorenej časti kryhy. Ak kryha pláva na povrchu, musí platiť rovnováha síl:  G  + F_v  = 0  , pričom tiažová sila  G = m_ľ g = r_ľ V g = r_ľ (V₁ + V₂) g   ,

 

vztlaková sila

 

 .

 

Za rovnováhy sa budú veľkosti síl rovnať (smery sú opačné):

 

 

 

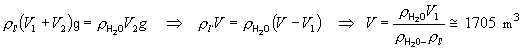
pričom sme dosadili  z tabuliek hustotu morskej vody:     

 

 

r _H2O = 1,025.10³ kg m ^–3   a  hustotu  ľadu  r _ľ = 916,8 kg m^–3 .

 

 

 

Príklad 3.8  Keď do valcovej nádoby s vodou položíme na jej hladinu zhora otvorenú železnú škatuľku, hladina vody v nádobe sa zvýši o  l = 2 cm. O koľko sa zníži hladina keď škatuľku potopíme?

 

Riešenie:

Ak škatuľka pláva na povrchu vytlačí časť vody s objemom V_H2O = Sl ,  rovným objemu ponorenej časti škatuľky, kde S je prierez dna nádoby, l – výška zdvihnutia hladiny vody.

 

Musí platiť rovnováha síl:

 

 

 Odtiaľ 

 

 .

 

Ak je škatuľka ponorená celá, objem vytlačenej vody je rovnaký ako celý objem materiálu škatuľky. Hladina sa zdvihne o výšku  x :

 

 

Zníženie hladiny