Other Ab Initio Computational Methods

The computation of energies, geometries, wavefunctions, etc. by the Hartree-Fock method has several disadvantages which mean it is not suited to all problems. The main problems are:

  1. Expense. Calculating then storing N4 two-electron integrals is time- and memory-consuming.
  2. Applicability. Certain molecules or transition states have an electronic structure which cannot be described by a Slater Determinant.
  3. Accuracy. The energies computed with HF methods are quite accurate in absolute terms (Total energies). However, differences in energy are much less well reproduced.

Semi-Empirical Methods

Hartree-Fock:

\[ E_{SD}=\int \Psi_{SD}\hat{H}_{elec}\Psi_{SD} d\mbox{x} \] \[E_{SD}=\sum_i^{n_{elec}} h_{ii} + \sum_{i}^{n_{elec}}\sum_{j>i}^{n_{elec}}(J_{ij}-K_{ij}) \] \[ K_{ij} = \iint \psi_i(r_1)\psi_j(r_2) \frac {1}{r_{12}} \psi_i(r_2)\psi_j(r_1) dr_1dr_2 \] \[ \mathcal{O}(n_{basis}^4) \;\; (ab|cd) = \iint \phi_a(r_1)\phi_b(r_1)\frac{1}{r_{12}}\phi_c(r_2)\phi_d(r_2) \; dr_1dr_2 \]

Instead of this, an approximate expression can be used instead of H, which ultimately leads to approximate expressions being used for hii, Jij and Kij, requiring the computation of far fewer integrals. Some of the integrals are given empirical values, adjusted to reproduce the known properties of certain simple atoms and molecules.

There are different ways of introducing the approximations, ranging from the extremely crude (Hückel theory) to the extremely sophisticated (PM3, AM1), and including models such as MNDO, CNDO, ...

These methods give wavefunctions, like ab initio methods, so can be used to predict a certain number of properties beyond the mere energy of the system. They can be applied, on a routine basis, even to very large molecules.

Electron Correlation

Problems (2) and (3) above are really two not-completely-distinct parts of the same problem: The Molecular Orbital Approximation is an approximation. A wavefunction cannot be factorised !! Equivalently, electrons do not move independently one from another: their motion is said to be Correlated. Ab Initio methods which include this effect are said to be Correlated methods; they describe electron correlation.

How can one expand an unfactorisable wavefunction in terms of atomic orbitals? By taking a Linear Combination of Slater Determinants:

\[ \Psi_{\mbox{non factorisable}} = \sum_{i}^{n_{SD}} c_i \Phi_{i,\mbox{SD}} \]

The energy of such a wavefunction is always lower than that of the Hartree-Fock wavefunction. The difference in energy is called the correlation energy.

Applicability

Some wavefunctions need more than one determinant to describe them properly even in a qualitative sense. A simple example is the H2 molecule at long bond distances:

\[ \Psi_{\mbox{HF}}(\mbox{H}_2,r=\infty) = \left \{ \begin{array}{l} | \chi_{\sigma_g}(\mbox{x}_1)\chi_{\sigma_g}(\mbox{x}_2) \rangle \\ \mbox{ } \\ | \psi_{\sigma_g}(r_1)\overline{\psi_{\sigma_g}(r_2)} \rangle \end{array} \right. \] \[ \psi_{\sigma_g} = \frac{1}{\sqrt{2}}(\phi^A_{1s}(r) + \phi^B_{1s}(r)) \] \[ \Psi_{\mbox{HF}}(\mbox{H}_2) = (\phi^A_{1s}(r_1) + \phi^B_{1s}(r_1)) \times (\phi^A_{1s}(r_2) + \phi^B_{1s}(r_2)) \]

\[ \Psi_{\mbox{HF}}(\mbox{H}_2) = \left \{ \phi^A(r_1)\phi^A(r_2) + \phi^B(r_1)\phi^B(r_2) + \phi^A(r_1)\phi^B(r_2) + \phi^B(r_1)\phi^A(r_2) \right \} \]

\[ \Psi_{\mbox{HF}}(\mbox{H}_2) = \mbox{H}^-\mbox{H}^+ + \mbox{H}^+\mbox{H}^- + 2 \times \mbox{H}^{\bullet}\mbox{H}^{\bullet} \]

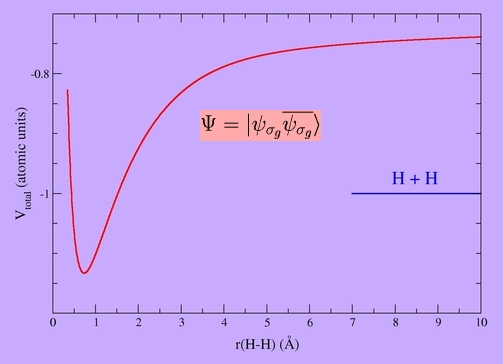
The correct wavefunction only contains the neutral terms. This cannot be obtained by a single determinant:

\[ \Psi_{\mbox{true}}(\mbox{H}_2,r=\infty) = \left \{ \begin{array}{l} \phi^A(r_1)\phi^B(r_2) + \phi^B(r_1)\phi^A(r_2) \\ \mbox{ } \\ | \psi_{\sigma_g}(r_1)\overline{\psi_{\sigma_g}(r_2)} \rangle - | \psi_{\sigma_u}(r_1)\overline{\psi_{\sigma_u}(r_2)} \rangle \end{array} \right. \] \[ \psi_{\sigma_u} = \frac{1}{\sqrt{2}}(\phi^A_{1s}(r) - \phi^B_{1s}(r)) \]

Allowing the wavefunction to be given as a sum of these two determinants yields a qualitatively correct (Multi-Configuration Self-Consistent Field, MCSCF) wavefunction:

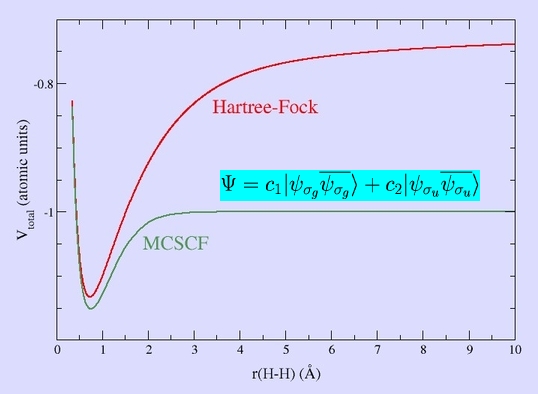
Similar results can be obtained using the Valence-Bond Method, but this is used more seldom in computations due to its algorithmic inconvenience.

Similar Multi-Reference problems are met whenever bonds are strongly broken. For example, the Hartree-Fock method will be completely inappropriate to study the cis to trans isomerisation of cyclopropane:

This situation, known as Non-Dynamic Correlation, can also occur for excited states, or for molecules with an unusual electronic structure.

Accuracy

The Hartree-Fock method allows electrons (especially those of opposite spin) to approach one another because it treats the Coulombic repulsion between electrons in an average way only:

\[ P_{\mbox{HF}}(r_1 = r_2) \neq P_{\mbox{true}}(r_1 = r_2) = 0 \]

We have mentioned before how any function can be expanded as a linear combination of suitable functions. In this way, the "true" wavefunction can always be expanded as a sum of Slater Determinants. It is not possible to give a simple pictorial representation of how this leads to the correct behaviour of the electron-electron relative position probability... but it does!

The most straightforward way of computing correlated wavefunctions is the Configuration Interaction (CI) method, which uses the variational method to optimise the coefficients of the different Determinants. Usually, one starts from a Hartree-Fock wavefunction, and because of computational expense, includes only the Slater Determinants which most ressemble the Hartree-Fock Determinant:

\[ \Psi_{\mbox{HF}}=\Phi^0 = | \chi_a\chi_b\chi_c\ldots\chi_m \rangle \] \[ \Phi_b^s = | \chi_a\mathbf{\chi_s}\chi_c\ldots\chi_m \rangle \] \[ \Phi_{bc}^{st} = | \chi_a\mathbf{\chi_s\chi_t}\ldots\chi_m \rangle \] \[ \Psi_{\mbox{CI}} = c_0\Phi^0 + \sum_{a,s}c_a^s\Phi_a^{s} + \sum_{a,b,s,t}c_{ab}^{st}\Phi_{ab}^{st} + \sum_{a,b,c,s,t,u}c_{abc}^{stu}\Phi_{abc}^{stu} \ldots \]

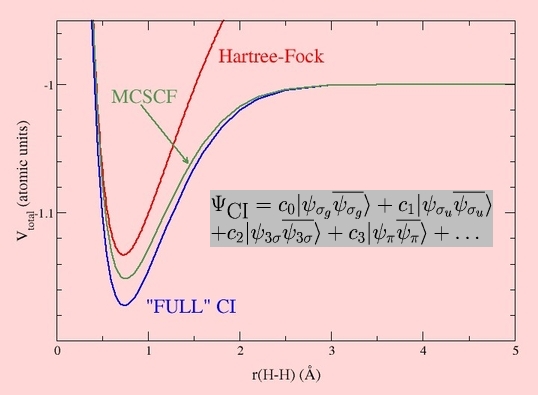
This effect is known as Dynamic Correlation, and plays an important role whenever quantitative relative energies are needed - e.g. between two fragments and the corresponding bonded species, or between two isomers, etc. As well as the CI method, other approaches can be used to introduce excited determinants:

Density Functional Theory

As is so often the case with mathematical expressions in physics/chemistry, the Schrödinger equation can be recast in many different ways, which although they are all fundamentally the same, are each suggestive of different approximate methods of solution. We have been using the "traditional" method to solve the Schrödinger equation until now, but will briefly mention another approach, Density Functional Theory.

Kohn and Hohenberg showed in 1964 that all the properties of a (molecular) system, including its energy, can in principle be deduced once one knows the Electronic Density function rho of the system. The energy is a "function" of the density function, which is often called a "Functional":

\[ E=\mathcal{E}[\rho(r)] \]

Unfortunately, this in only an "in principle" result, which fundamentally boils down to the fact that from the density it is possible to deduce the form of the Hamiltonian - from which all the other properties can be derived by the traditional methods. However, casting the problem in this form does enable one to put forward some approximate expressions giving the energy as a function of the density. Coupled with a form of the Variational Method, this enables one to compute densities and energies for molecular systems.

The design of approximate energy functionals has become very sophisticated, and some have been shown to yield very accurate results (much better than HF theory, for example) for a broad range of systems. Density Functional methods are now a method of choice in computational electronic structure theory.

Click here to return to the list of online lectures

Click here to return to the previous Section

Click here to go on to the next Section

This page created by Jeremy Harvey, Bristol, 2000.