7.2.3 Termodynamické procesy

Na opis rovnovážneho stavu sústavy častíc sa používajú stavové veličiny, ktorých vzájomný súvis vyjadruje stavová rovnica.

V sústave prebiehajúce procesy môžeme rozdeliť z hľadiska ich vratnosti na:

· reverzibilné ( vratné ) procesy - po prebehnutí takéhoto procesu sa sústava môže sama, bez vonkajšieho vplyvu, dostať späť do východiskového stavu. Takým procesom je napríklad veľmi pomalá expanzia plynu uzavretého v nádobe s pohyblivou stenou. A potom opačný proces, veľmi pomalá kompresia tohoto plynu do pôvodného stavu. Proces musí byť tak pomalý, že plyn sa dostáva z počiatočného do konečného stavu a opačne sledom rovnovážnych stavov, ktoré plyn dosahoval po nekonečne malých zmenách týchto rovnovážnych stavov.

· ireverzibilné ( nevratné ) procesy - sústava sa nemôže sama, bez vonkajšieho vplyvu, dostať späť do východzieho stavu. Príkladom takéhoto procesu môže byť prudké stlačenie alebo expanzia plynu v nádobe.

Tieto procesy môžu v prírode prebiehať za rôznych špecifických podmienok.

a) Opíšeme proces prebiehajúci v sústave uzavretej v nádobe s konštantným objemom - izochorický dej. Všeobecne platí, že ak dodáme sústave teplo dQ, toto teplo sa rozdelí na časť dU, ktorá spôsobí zvýšenie vnútornej energie a časť , ktorou vykoná plyn prácu. Teda platí

(7.2.3.1 )

Elementárnu zmenu vnútornej energie v tomto vzťahu, množstva n mólov plynu pri zmene teploty o dT, môžeme zapísať a plynom vykonanú prácu pri zmene objemu o dV vzťahom dW¢ = pdV. Potom prejde vzťah 7.2.3.1 do tvaru

. ( 7.2.3.2 )

Za danej podmienky, že objem je konštantný (V = konšt.) je zmena objemu nulová (dV = 0 ), teda aj práca vykonaná plynom je nulová (dW¢ = 0 ). Potom sa teplo dodané sústave prejaví len zmenou vnútornej energie. Ak ešte za látkové množstvo dosadíme

,

vzťah 7.2.3.1 nadobudne tvary

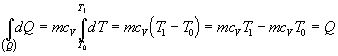( 7.2.3.3 )

.

Poslednú rovnicu môžeme slovne vyjadriť takto: Teplo dodané sústave pri izochorickom deji spôsobí len zmenu jej vnútornej energie.

b) Proces prebiehajúci v sústave pri konštantnej teplote - izotermický proces.

Pri sledovaní tohoto procesu budeme vychádzať zo vzťahu 7.2.3.2 .

Za danej podmienky, že teplota je konštantná (T = konšt.) je zmena teploty nulová (dT = 0 ), teda aj zmena vnútornej energie je nulová (dU = 0 ). Potom teplo dodané sústave, sa prejaví ako práca plynu, ktorú vykoná pri svojej expanzii. Rovnica 7.2.3.2 prejde do tvaru

alebo

.

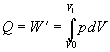Ak za tlak plynu dosadíme upravenú rovnicu Boylovho - Mariottovho zákona v tvare

, platí

.

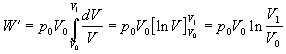Rovnica opisuje výpočet práce pri známych zmenách hodnôt tlaku a objemu plynu.Túto prácu je možné vypočítať využitím posledného vzťahu aj pri zadaní iných stavových veličín, využitím vhodného tvaru stavovej rovnice. Napríklad

· ,

· ,

· ,

a podobne.

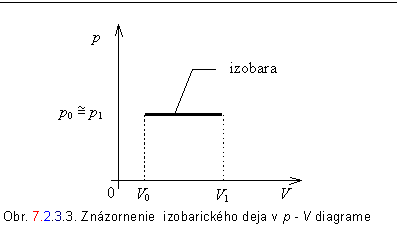
c) Proces pri konštantnom tlaku - izobarický proces.

Za danej podmienky, že tlak je konštantný (p = konšt.) je aj jeho zmena nulová (dp = 0 ). Potom, teplo dodané sústave sa prejaví zvýšením vnútornej energie a prácou, ktorú plyn vykoná pri svojej expanzii. Rovnicu 7.2.3.2 môžeme napísať v tvare

,

alebo

.

V poslednom vzťahu sme označili H = U + pV, kde H sme označili novozavedenú fyzikálnu veličinu nazvanú entalpia sústavy. Jeho integráciou dostaneme

.

Slovne: Teplo prijaté sústavou za konštantného tlaku sa rovná prírastku entalpie sústavy.

d) Proces prebiehajúci bez výmeny tepla medzi sústavou a okolím - adiabatický proces. V prírode sa vyskytujúce procesy, ktoré prebiehajú dostatočne rýchlo môžeme považovať za adiabatické.

Za danej podmienky, že teplo dodané sústave je nulové (dQ = 0 ), rovnica 7.2.3.1 nadobúda tvar

,

alebo

. ( 7.2.3.4 )

Nájdime teraz diferenciály oboch strán stavovej rovnice pV = nRT za podmienky, že n,R sú konštanty a vyjadrime z nej diferenciál teploty

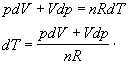
Dosadením do rovnice 7.2.3.4 za dT upravíme vzniknutý vzťah jednoduchými matematickými úpravami

.

Poslednú úpravu sme vykonali využitím platnosti rovnice

,

paragraf 7.1.5. Ďalej vykonáme separáciu premenných a rovnicu zintegrujeme ako neurčitý integrál

,

kde lnC je zvolená integračná konštanta. Využijeme poznaty z matematiky o odlogaritmovaní a dostávame

. ( 7.2.3.5 )

Vzťah 7.2.3.5 nazývame Poissonova rovnica. Udáva vzájomnú závislosť tlaku a objemu plynu pri adiabatických zmenách.

Vzťah môžeme napísať aj v nasledujúcom tvare

konštanta .

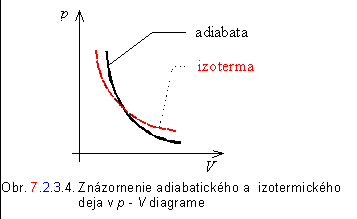
Grafickú závislosť tlaku a objemu pri adiabatickom deji a na porovnanie aj pri izotermickom deji znázorňuje obr. 7.2.3.4.

Príklad 7.2.3.1

Akú hmotnosť má hélium ( molárna hmotnosť M = 4.10^-3 kg.mol^-1 ), ktoré sme zohriali dodaním tepla 209 J z teploty 60 ⁰C na 80 ⁰C pri konštantnom objeme ?

Riešenie :

V súlade so zadaním označíme Q = 209 J, t₁ = 60 ⁰C a t₂ = 80 ⁰C. Pre výpočet použijeme vzťah 7.2.3.3 v tvare

.

Úpravou Mayerovho vzťahu 4.2.2.3 získame vzťah pre výpočet c_V :

.

Pri úprave sme využili vzťah pre výpočet Poissonovej konštanty 7.1.14 . Po dosadení do východzieho vzťahu dostávame :

.

Vzťah matematicky upravíme a dosadíme číselné hodnoty. Hodnotu Poissonovej konštanty vypočítame využitím empirického vzťahu 7.1.14, pričom zo zadania príkladu vieme, že počet stupňov voľnosti i = 3. Prevod teploty z Celziovej na Kelvinovu sme urobili ako v príklade 7.2.1.2 .

.

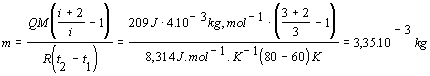Za daných podmienok sme zohriali 3,35.10^-3 kg hélia.

Kontrolné otázky

1. Aký je rozdiel medzi reverzibilným a ireverzibilným procesom?

2. Prečo pri izochorickom deji plyn prácu nemôže konať?

3. Čo nazývame entalpiou sústavy?

4. Aká je fyzikálna jednotka entalpie?

5. Akú rovnicu by ste považovali pri izotermickom deji za ekvivalent Poissonovej rovnice pri adiabatickom deji?

6. Izobaricky zohrejme 5kg oxidu uhličitého z 10°C tak, aby počas rozpínania vykonal prácu 49050J. Na akú výslednú teplotu sa plyn zohreje? Molárna hmotnosť oxidu uhličitého je 44.10 ^-3 kg.mol ^-1. (T=334,9K)

7. Do nádoby s pevnými stenami umiestnime 20 l vodíka. Koľko tepla mu musíme dodať, aby sa jeho tlak zvýšil z 5066,25kPa na 6079,5kPa? Vodík má molárnu hmotnosť 2.10 ^-3 kg.mol ^-1 a hmotnostnú tepelnú kapacitu 10130 J.kg ^-1.K ^-1. ( Q=49,383kJ )

8. Počas stláčania 5 l vzduchu z počiatočného tlaku 101kPa sa odovzdal okoliu 1kJ tepla. Aký mal tlak a aký objem zaberal vzduch po stlačení, ak dej prebiehal izotermicky? ( p=731,88kPa, V=6,9.10 ^-4 m³ )

9. Akú prácu vykoná 2,5m³ vzduchu s teplotou 32°C a tlakom 455962Pa, keď sa adiabaticky rozopne tak, že jeho teplota klesne na 15°C. Hmotnostná tepelná kapacita vzduchu je 728 J.kg ^-1.K ^-1 a molárna hmotnosť je 28,45.10 ^-3 kg.mol ^-1. ( W=158,5kJ )