Odvodenie van der Waalsovej stavovej rovnice

Objem častíc sa prejaví takto: Častice v skutočnosti nemajú k dispozícii objem nádoby V ale objem (V-b), kde b je 4-násobok súhrnného objemu častíc. Dostali sme korekciu stavovej rovnice ideálneho plynu na objem častíc:

(a)

0

E

r

r₀

Dvojica susedných častíc plynu je mechanická sústava dvoch hmotných bodov s potenciálnou energiou, ktorej závislosť od vzdialenosti medzi časticami je ukázaná na obr.

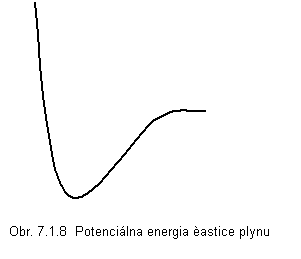
7.1.8. Vzdialenosť prislúchajúca minimu potenciálnej energie je rovnovážna vzdialenosť. Ak sa častice dostanú do vzdialenosti r < r₀ , sila medzi časticami je odpudivá, ak r > r₀ sila pôsobiaca medzi časticami je príťažlivá. Závislosť sily medzi časticami od ich vzájomnej vzdialenosti je nesúmerná, častice sú oveľa dlhšiu dobu ďalej od seba ako je rovnovážna vzdialenosť, a preto prevládajú v plyne príťažlivé sily medzi časticami. Prejavuje sa to tak, ako by v plyne pôsobil navyše tlak p_i (tzv. vnútorný tlak), ktorý sa pridáva k tlaku, ktorým pôsobí plyn na steny nádoby. Odhadneme vnútorný tlak.

Príťažlivé sily na časticu, ktorá je ďalej od stien sa pri chaotickom pohybe rušia, pretože táto častica je zo všetkých strán obklopená časticami, ktoré ju k sebe priťahujú. Situácia inakšie vyzerá v tesnej blízkosti steny. Na vrstvu častíc (označme ju A), ktorá je v priamom susedstve so stenou, pôsobia príťažlivé sily od vrstvy častíc plynu, ktorá s ňou priamo susedí (vrstva B). Na vrstvu A pôsobia teda príťažlivé sily len z jednej stranu (od steny nádoby nie), vrstva A je vťahovaná dovnútra. Počet častíc vo vrstve A je úmerný koncentrácii n. Počet častíc vo vrstve B je tiež úmerný n. Sila medzi vrstvami je úmerná počtu častíc v oboch vrstvách, t.j. n². Vnútorný tlak úmerný tejto sile bude tiež úmerný n². Koncentrácia sa zase rovná počtu častíc v nádobe (ktorý je konštantný) delenom objemom nádoby, t.j. n = N/V a vnútorný tlak môžeme napísať ako

Stavová rovnica bude teraz vyzerať takto:

(7.1.30)

Výpočet ukazuje