7.1.4 Stavová rovnica ideálneho plynu
Z rovnice (7.1.2) vyplýva (po jej vynásobení
objemom nádoby)
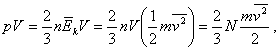
kde N je počet častíc plynu
v nádobe. V rovnici vystupuje stredná kinetická energia jednej
častice násobená počtom častíc, čo dáva celkovú kinetickú energiu, ktorá ako
vieme, sa rovná vnútornej energii plynu. Môžeme napísať
![]() (7.1.6)
(7.1.6)
Vezmime si 1 mól plynu. Jeden mól je také množstvo látky, ktoré obsahuje NA
častíc (molekúl, atómov). Potom N = NA = 6,023.1023
mol-1 , čo je Avogadrova
konštanta, ktorá predstavuje počet častíc v jednom móle látky (plynu).
Vzťah (7.1.6) sa zmení
![]() (a)
(a)
Súčin dvoch konštánt NAk
dáva novú konštantu, ktorú nazývame molárnou
plynovou konštantou a jej hodnota je R
= 8,317 J.K-1.mol-1. Takže pre jeden mól plynu máme
pV = RT , (7.1.7)
čo je stavová
rovnica ideálneho plynu pre jeden mól plynu. Ak máme iný počet mólov, treba pravú stranu
(7.1.7) násobiť týmto počtom. Veličiny p,
T určujú stav plynu, nazývame ich stavovými veličinami. Rovnica (7.1.7) sa
môže prepísať do tvaru
![]() (7.1.7a)
(7.1.7a)
kde indexy 1, 2 zodpovedajú dvom rôznym stavom plynu. Táto rovnica platí
pre každé množstvo plynu. Z rovnice (a) vyplýva
![]()
čo znamená, že všetky plyny majú pri rovnakých podmienkach (teplote
a tlaku) rovnakú koncentráciu častíc. Pri normálnych podmienkach (Tn = 273,15 K; pn = 1,01325.105
Pa) máme
![]() (7.1.8)
(7.1.8)
Táto hodnota sa tiež nazýva Loschmidtova
konštanta. Nezávisí od druhu plynu.
Stavová
rovnica (7.1.7), (7.1.7a) platí pre každý dej v plyne. Z tejto
rovnice môžeme získať rovnice pre špeciálne prípady:
a)
izotermický dej pri T = const. Potom
![]() (7.1.9)
(7.1.9)
Tieto
rovnice sú matematickým vyjadrením Boyle-Mariottovho
zákona. Indexy 1, 2
v druhej rovnici zodpovedajú dvom rôznym stavom plynu.
b)
izobarický dej pri p = const. Potom
![]() (7.1.10)
(7.1.10)
c)
izochorický dej pri V = const. Potom
![]() (7.1.11)
(7.1.11)
Rovnice v bodoch b, c sú matematickým vyjadrením Gay-Lussacových zákonov pre izobarický
a izochorický dej.
__________________________________
Príklad
7.1.4.1
V nádobe s objemom 1 m3 je kyslík s teplotou 27
°C a tlakom 105 Pa. Napíšte stavovú rovnicu pre tento stav.
Aká je hmotnosť plynu v nádobe?
Riešenie:
Použijeme (7.1.7), avšak pravú stranu musíme násobiť
počtom mólov. Budeme mať
![]()
kde m je hmotnosť plynu a m je hmotnosť 1 mólu plynu. Pre molekulu O2 je to 2 x atómová
hmotnosť kyslíka x hmotnosť nukleónu x Avogadrova konštanta = 2.16.1,67.10-27.6,02.1023
= 0,032 kg (poznámka: táto hmotnosť vyjadrená v gramoch sa číselne (nie
rozmerom) rovná relatívnej atómovej hmotnosti). Hmotnosť plynu v nádobe je
![]()
Po dosadení číselných hodnôt m = 1,28 kg.
________________________________
Kontrolné otázky
1. Pomocou
vzťahov (7.1.8) a pV = NAkT
vypočítajte hodnotu Avogadrovej konštanty.
2. V príklade
7.1.4.1 sme vypočítali počet mólov pomocou hmotností. Dá sa určiť počet mólov
plynu v nádobe pomocou objemov?
3. V oceľovej
nádobe ohriatím zvýšime teplotu plynu. Ktoré parametre plynu sa ešte zmenia?