6.1.9 Rozklad kmitov, harmonická analýza

Opakom skladania kmitov rovnakého smeru je rozklad kmitov na násobky základnej frekvencie – Fourierova analýza. Fourierova analýza má veľký praktický význam, a to hlavne v oblasti analýzy zvukov, spracovania impulzných signálov, ako aj v moderných spektroskopických prístrojoch.

Podľa Fourierovej vety každú periodickú funkciu s periódou T a s konečným počtom nespojitostí možno vyjadriť v tvare

(6.1.9.1)

kde w = 2p/T a konštanty A₀, A_k, B_l sú určené rovnicami

(6.1.9.2)

(6.1.9.3)

(6.1.9.4)

Platnosť týchto vzťahov si ľahko overíme ak využijeme vzťahy známe z integrálneho počtu a to

(6.1.9.5)

(6.1.9.6)

(6.1.9.7)

Ak budeme integrovať rovnicu (6.1.9.1) v intervale <0, T>, všetky členy okrem A₀ na pravej strane tejto rovnice vypadnú a dostávame tvrdenie (6.1.9.2). Ak rovnicu (6.1.9.1) vynásobíme cos(kw t) a integrujeme v rovnakom intervale vypadnú všetky členy v ktorých vystupuje funkcia sin a nenulový bude iba člen pri A_k, z čoho priamo vyplýva tvrdenie (6.1.9.3). Rovnicu (6.1.9.4) dostávame analogicky, ak (6.1.9.1) vynásobíme sin(lw t) a integrujeme v intervale <0, T>. Čím väčší počet členov v rozvoji (6.1.9.1) zoberieme do úvahy, tým presnejšie reprodukujeme pomocou harmonických funkcií periodickú funkciu f(t).

______________________________________

Príklad 6.1.24

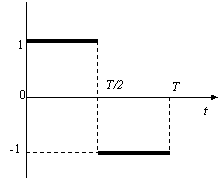
Rozložte jednotkovú periodickú funkciu f(t), znázornenú na obr.6.1.17 do harmonických zložiek.

Riešenie:

Obr. 6.1.17

Matematicky vyjadríme danú funkciu nasledovne:

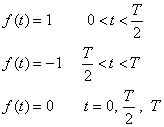
Pre funkciu f(t) platí:

.

Hľadáme amplitúdy A₀, A_k, B_k :

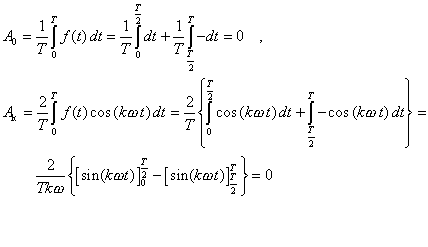
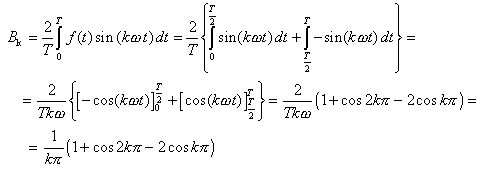
Pre nepárne hodnoty k = 1, 3, 5, 7, ... dostaneme

pre párne = 2, 4, 6, ... je B _k = 0 .

Hľadaný rozvoj funkcie bude mať tvar: