6.1.8.3 Skladanie kolmých kmitov

Pri skladaní kmitov rôzneho smeru sa uplatňuje rovnako ako v predchádzajúcom prípade princíp superpozície. Výsledné kmitanie bude vektorovým súčtom dielčích kmitov. Nech hmotný bod môže konať kmitavé pohyby v osi x a v osi y. Zvoľme si počiatok času tak, aby fázová konštanta jedného z pohybov bola nulová a ukážeme si skladanie kolmých kmitov na príklade skladania kmitov rovnakej frekvencie, rôznej amplitúdy a fázy. Pre dielčie kmity platí:

(6.1.8.3.1)

Tieto rovnice sú parametrickými rovnicami trajektórie, po ktorej sa hmotný bod bude pohybovať. Jej tvar bude závisieť od amplitúd jednotlivých kmitov a rozdielu fáz. Rovnicu trajektórie y = f(x) nájdeme vylúčením času. Z prvej rovnice máme

Použijeme súčtový vzorec pre funkciu cos(wt +j), do ktorého dosadíme predchádzajúce vzťahy a po elementárnych matematických úpravách dostávame

(6.1.8.3.2)

Z analytickej geometrie vieme, že posledná rovnica predstavuje všeobecný tvar rovnice elipsy. Nájdime tvar trajektórie pre niektoré špeciálne prípady.

a) Nech j = 0. Potom

a trajektória je rovnicou priamky. Kmitajúci bod sa pohybuje po priamke prechádzajúcej počiatkom súradníc a jeho vzdialenosť od počiatku je

(6.1.8.3.3)

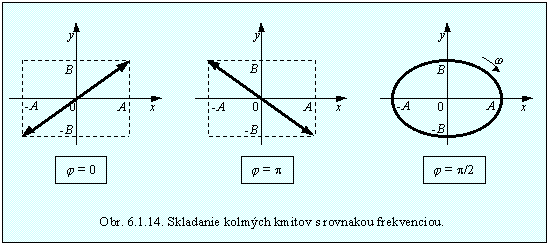
Výsledný pohyb je pohyb po priamke s frekvenciou w .

b) Nech fázový rozdiel je j = ± p. Rovnica (6.1.8.3.2) má v takomto prípade tvar

a pohyb sa koná po priamke zobrazenej na obr. 6.1.14.

c) Nech fázový rozdiel je j = ± p/2. Rovnica (6.1.8.3.2) prechádza na rovnicu elipsy, ktorej poloosi majú veľkosti A a B. (Obr. 6.1.14)

Pohyb sa bude konať v smere hodinových ručičiek, ak j = +p/2, resp. proti smeru otáčania hodinových ručičiek, ak j = –p/2.

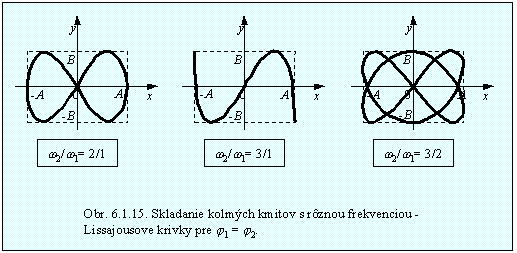
Ak frekvencie skladaných kolmých kmitov nie sú rovnaké a ak pomer ich frekvencií sa dá vyjadriť ako podiel prirodzených čísel, výsledný pohyb sa koná po krivkách, ktoré nazývame Lissajousove krivky. Príklad Lissajousových kriviek je na obr. 6.1.15.

______________________________________

Príklad 6.1.26

Dva jednosmerné kmitavé pohyby s rovnakou periódou a s amplitúdami A₁ = 0,03 m a A₂ = 0,05 m sa skladajú do výsledného pohybu s amplitúdou A = 0,07 m. Vypočítajte rozdiel fáz oboch pohybov.

Riešenie:

Okamžité výchylky jednotlivých kmitavých pohybov sú:

x₁ = A₁ cos(wt + a ₁), x₂ = A₂ cos(wt + a₂)

Máme nájsť fázový rozdiel, t. j. D = (wt + a ₁)– (wt + a ₂) = a ₁ –a₂.

Podľa princípu superpozície pre výsledné kmitanie platí:

x = x₁+ x₂ = A₁ cosw t cos a ₁ – A₁ sinw t sina ₁ + A₂ cosw t cos a ₂ – A₂ sinw t sina ₂

x = cosw t (A₁cos a ₁ + A₂cos a ₂) – sinw t (A₁ sina ₁ + A₂ sina ₂) = A cos(w t + a ),

kde sme zaviedli substitúcie:A sina = A₁ sina ₁ + A₂ sina ₂ , A cosa = A₁ cosa ₁ + A₂ cosa ₂.

Umocnením týchto rovníc a ich sčítaním dostaneme:

.

Odtiaľ vyjadríme rozdiel fáz obidvoch pohybov:

Poznámka: Kmity rovnakej frekvencie sme v časti (6.1.8.1) skladali pomocou vektorového zobrazenia kmitavého pohybu. Alternatívou, ako sme mohli vidieť v tomto riešení je využiť pri skladaní takýchto kmitov trigonometrické vzťahy.

Príklad 6.1.27

Dva harmonické pohyby rovnakého smeru, rovnakej amplitúdy a fázovej konštanty s periódami T₁ = 0,0046 s a T₂ = 0,0045 s sa skladajú do výsledného pohybu. Nájdite periódu výsledného kmitavého pohybu a periódu rázov.

Riešenie:

Okamžité výchylky skladaných pohybov sú:

x₁ = A cos(w₁ t + a ), x₂ = A cos(w₂ t + a )

V časti (6.1.8.2) sme si ukázali, že okamžitú výchylku výsledného pohybu dostaneme na základe princípu superpozície:

kde A(t) je časovo závislá funkcia, ktorej absolútna hodnota určuje amplitúdu výsledného kmitania a priebeh tejto funkcie bude vplývať tiež na fázu výsledného kmitania. Uhlová frekvencia výsledného pohybu je:

.

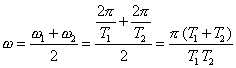Potom perióda výsledného pohybu:

Perióda rázov je určená vzťahom (6.1.8.2.6) a rovná sa

Príklad 6.1.28

Nájdite dráhu výsledného pohybu, ktorý vznikne pri skladaní dvoch navzájom kolmých harmonických kmitavých pohybov s amplitúdami A₁ = 0,03 m , A₂ = 0,04 m, s rovnakými periódami, keď rozdiel fáz oboch pohybov je j = p /2.

Riešenie:

Kmitavé pohyby v dvoch navzájom kolmých smeroch x, y môžeme popísať rovnicami:

x = A₁ cos(wt + a₁ ), y = A ₂ cos(w t + a₂) ,

pričom rozdiel fáz Da = (w t + a₁ ) – (w t + a₂) = (a₁ –a₂) = p /2 .

Potom x = A₁ cos(w t + a₂ + p /2) = – A ₁ sin(w t + a₂) .

Upravme teraz pôvodné rovnice do tvaru:

Rovnice umocníme, sčítame a dostávame

čo je rovnica elipsy s hlavnými osami v smeroch x a y. V našom prípade bude mať tvar:

.

Dráha výsledného pohybu je elipsa.

Kontrolné otázky k časti 6.1.8

1. Podľa akého princípu nájdeme výsledné kmitanie pri skladaní viacerých kmitavých pohybov?

2. Kedy hovoríme o kmitoch, že sú vo fáze, a kedy je ich fáza opačná?

3. Môže nastať pri skladaní kmitov rovnakého smeru stav, že sa kmity navzájom rušia? Aké podmienky by pri tom museli spĺňať dielčie kmity?

4. Pri skladaní akých kmitov dochádza k vzniku rázov?

5. Aká je frekvencia rázov?

6. Dve husľové struny kmitajúce s rovnakou amplitúdou vydávajú tóny s frekvenciami f₁ = 440 Hz, f₂ = 436 Hz. Aká je frekvencia, ktorú počuje pozorovateľ? Koľko rázov počuje pozorovateľ za sekundu?

7. Ako voláme krivky, ktoré vzniknú pri skladaní kolmých kmitov rôznych frekvencií?

8. Uvažujte dva kmity: x₁ = A sin(w t) , x₂ = A sin(w t +p/2). Zložením týchto dvoch kmitov vznikne kmitanie. Aká bude jeho výsledná amplitúda a fázový posun? Výsledok určite využitím vektorového zobrazenia kmitavých pohybov.

9. Dva navzájom kolmé harmonické kmity : x = 3 sin w t, y = 4 sin w t, (cm, s) sa skladajú do výsledného kmitania. Aká bude jeho amplitúda?

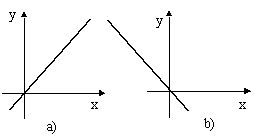
Obr. 6.1.16

10. Uvažujte skladanie dvoch navzájom kolmých harmonických kmitov s rovnakými amplitúdami a uhlovými frekvenciami. Aký musí byť fázový rozdiel a medzi skladanými kmitmi, aby vzniklo výsledné harmonické kmitanie v priamke podľa obr. 6.1.16 (a), (b)?

11. Uvažujte skladanie dvoch navzájom kolmých harmonických kmitov s rôznymi amplitúdami a rovnakými uhlovými frekvenciami. Aký musí byť fázový rozdiel a medzi skladanými kmitmi, aby výsledné harmonické kmitanie bolo eliptické?

12. Uvažujte skladanie dvoch navzájom kolmých harmonických kmitov s rovnakými amplitúdami a uhlovými frekvenciami. Aký musí byť fázový rozdiel a medzi skladanými kmitmi, aby výsledný pohyb bol po kružnici?

Úlohy k časti 6.1.8

6.2.29 Dva jednosmerné kmitavé pohyby s rovnakými amplitúdami aj periódami sa skladajú do výsledného pohybu s nezmenenou amplitúdou a periódou. Vypočítajte rozdiel fáz medzi kmitavými pohybmi.

6.2.30 Dva harmonické kmitavé pohyby s frekvenciami f₁ = 40 s^–1 a f ₂ = 45 s^–1 sa skladajú do výsledného pohybu. Vypočítajte frekvenciu rázov, keď amplitúdy ako aj fázové konštanty obidvoch pohybov sú rovnaké.

6.2.31 Vypočítajte celkovú energiu hmotného bodu s hmotnosťou m = 0,01 kg, keď koná dva navzájom kolmé kmitavé pohyby s amplitúdami A₁ = 0,03 m, A₂ = 0,04 m, s rovnakými frekvenciami f ₁ = f ₂ = f = 5 s^–1 a tiež s rovnakými fázovými konštantami. Určte krivku, po ktorej sa pohybuje hmotný bod.