6.1.8.2 Skladanie kmitov rôznej frekvencie

Majme dva kmitavé pohyby v smere osi x, ktorých frekvencie sú rôzne. Nech uhlová frekvencia prvého kmitania je w₁ a druhého w₂. Na odstránenie matematických komplikácií predpokladajme, že fázová konštanta obidvoch kmitaní je nulová a rovnaká je aj amplitúda kmitov. Okamžité výchylky skladaných pohybov sú:

x₁ = A₀ cos(w₁ t ), x₂ = A₀ cos(w₂ t )

Okamžitú výchylku výsledného pohybu dostaneme na základe princípu superpozície :

(6.1.8.2.1)

Využili sme pri tom vzťah známy z trigonometrie a to

Prvý súčiniteľ v (6.1.8.2.1) (v zátvorke) sa v čase mení oveľa pomalšie ako druhý. Súvisí preto s amplitúdou a svojim znamienkom ovplyvňuje tiež fázu kmitu. Výsledný pohyb môžeme chápať ako kmitanie s uhlovou frekvenciou (w₁ +w₂)/2 a s pomaly sa meniacou amplitúdou. Amplitúda je definitoricky kladné číslo, preto

. (6.1.8.2.2)

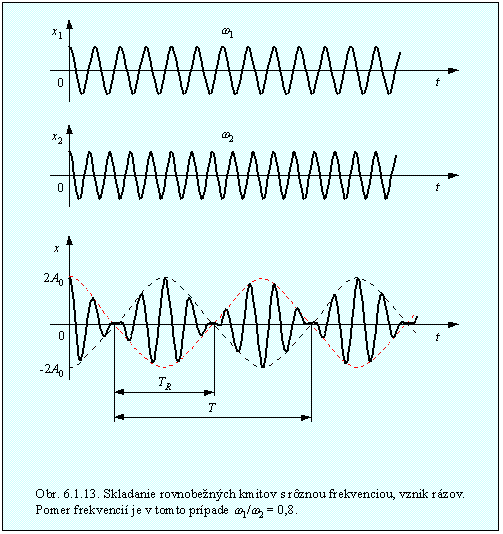
Výsledné kmitanie, aj priebeh amplitúdy sú ukázané na obr. 6.1.13.

Uhlová frekvencia výsledného pohybu je

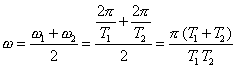(6.1.8.2.3)

a perióda výsledného pohybu je

(6.1.8.2.4)

Všimnime si teraz bližšie amplitúdu výsledného kmitania. Funkcia cos je periodická funkcia a za interval T = 2p/w nadobudne maximálnu kladnú, aj zápornú hodnotu. Absolútna hodnota takejto funkcie však za uvedený časový interval nadobudne svoju maximálnu hodnotu dvakrát. Frekvencia absolútnej hodnoty bude teda dvojnásobná. Zosilovanie a zoslabovanie amplitúdy pre skladaní kmitov blízkej frekvencie voláme rázy. Môžeme ich dobre pozorovať vtedy, keď frekvencie skladaných kmitov sa len málo líšia. Pre frekvenciu a periódu rázov dostávame

(6.1.8.2.5)

(6.1.8.2.6)