6.1.6 Tlmený harmonický pohyb.

Amplitúda ani energia netlmeného harmonického oscilátora od času nezávisia a pohyb takéhoto oscilátora by trval stále. Pri kmitaní reálnych objektov sa vždy viac, alebo menej stretávame s odporom prostredia a s trením. Kmity pri pôsobení trenia postupne zanikajú alebo, ako uvidíme v určitých prípadoch, napriek počiatočnej výchylke, alebo rýchlosti vôbec nevzniknú. Experimentálne môžeme tlmený kmitavý pohyb realizovať napríklad ponorením predchádzajúcej kmitajúcej sústavy – harmonického oscilátora do viskóznej kvapaliny ako je znázornené na obr.6.1.7.

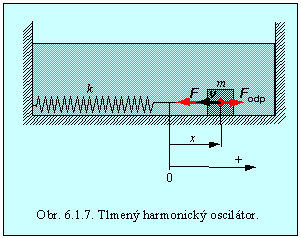
Predpokladajme, že odpor prostredia je priamo úmerný rýchlosti F_odp= – k´v , kde k´>0. Sila odporu prostredia smeruje proti rýchlosti, čo vyjadruje znamienko mínus v tomto výraze. Ak pôsobiaca návratná sila je priamo úmerná výchylke pohybová rovnica má tvar

(6.1.6.1)

Zaveďme substitúcie

.

Novú konštantu b nazývame koeficient útlmu. Konštanta w₀ je vlastná uhlová frekvencia, t.j. uhlová frekvencia netlmeného harmonického oscilátora. Po úprave dostávame pohybovú rovnicu v tvare

(6.1.6.2)

Riešenie rovnice hľadáme v tvare x = Ce^lt. Po dosadení tejto funkcie do predchádzajúcej rovnice dostávame charakteristickú rovnicu

ktorej riešením je

(6.1.6.3)

Dvom hodnotám l odpovedá všeobecné riešenie rovnice (6.1.6.2) v tvare lineárnej kombinácie

(6.1.6.4)

Podľa veľkosti tlmenia môžu nastať tri prípady:

i/ Tlmenie je veľké a b² – w ₀² > 0, potom obidve riešenia charakteristickej rovnice l_1,2 sú reálne čísla a x nemá žiadnu periodickú zložku. Teoreticky za čas t ® ¥ sa teleso dostane znovu do rovnovážnej polohy x = 0. Grafický priebeh závislosti x = x(t) je krivka (a) na obr. 6.1.8. Pri takomto veľkom tlmení o pohybe hovoríme, že je to aperiodický pohyb. Kmitanie vôbec nenastane.

ii/ Tlmenie je také, že b²– w ₀² = 0. V takomto prípade z matematiky vyplýva, že riešením rovnice (6.1.6.2) je funkcia x = e^-bt a aj funkcia x = t e^-bt (ľahko si overíme dosadením). Všeobecné riešenie je ich lineárnou kombináciou a má tvar

(6.1.6.5)

Tento pohyb nazývame medzný aperiodický pohyb. Zodpovedá mu krivka (b) na obr.6.1.8.

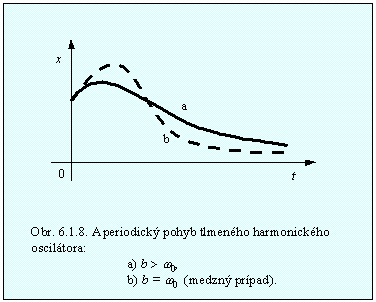
iii/ Tlmený kmitavý pohyb nastáva len pri malom tlmení, ak b²– w₀² < 0. Potom

Všeobecné riešenie pohybovej rovnice má tvar

(6.1.6.6)

Podobným postupom ako v prípade harmonického oscilátora dospejeme substitúciou a úpravou k reálnemu tvaru všeobecného riešenia

(6.1.6.7)

Uhlová frekvencia w je menšia, ako uhlová frekvencia pri netlmenom kmitaní tej istej sústavy a mení sa aj amplitúda, ktorá s časom exponenciálne klesá:

(6.1.6.8)

Priebeh kmitania a zmeny amplitúdy je ukázaný na obr.6.1.9.

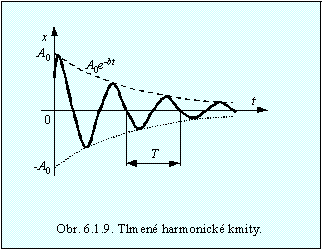
Prísne vzaté nemôžeme tlmený kmitavý pohyb pokladať za periodický pohyb, pretože kmitajúci bod nedosiahne svoju pôvodnú výchylku. Pohyb je kváziperiodický a o perióde T môžeme hovoriť iba ako o časovom intervale, za ktorý hmotný bod prechádza rovnovážnou polohou.

Perióda tlmených kmitov je

(6.1.6.9)

Platí T >T₀, kde T₀ je perióda vlastných kmitov. Ak je tlmenie malé, perióda sa prakticky rovná perióde netlmených kmitov. Zväčšovaním tlmenia perióda narastá.

Podiel amplitúd dvoch po sebe nasledujúcich maximálnych výchyliek označujeme l a nazývame útlm.

(6.1.6.10)

Prirodzený logaritmus útlmu je logaritmický dekrement útlmu d.

(6.1.6.11)

Zo závislosti amplitúdy na čase (6.1.6.8) vidíme, že amplitúda kmitov sa zmenší e-krát za časový interval rovnajúci sa 1/b. Potom prevrátená hodnota logaritmického dekrementu útlmu vyjadruje počet kmitov, počas ktorých sa amplitúda kmitov zmení e-krát. Čím väčší je logaritmický koeficient útlmu, tým menší je počet kmitov potrebný na určité zníženie amplitúdy.

V časti 6.1.4 sme zistili, že celková mechanická energia kmitajúceho oscilátora je úmerná štvorcu amplitúdy. Ak energia oscilátora s tlmením sa v čase t = 0 rovnala E₀, potom mechanická energia takéhoto oscilátora bude s rastúcim časom klesať, a to podľa rovnice

(6.1.6.12)

Vplyvom trenia dochádza k disipácii energie, mechanická energia kmitavého pohybu sa mení na energiu tepelnú a pohyb postupne zaniká. Ak v kmitajúcej sústave chceme pohyb udržať, musíme sústave vhodným spôsobom dodávať energiu. Na druhej strane práve tlmenie využívame v technickej praxi na odstránenie nežiadúcich vibrácií.

______________________________________

Príklad 6.1.14

Logaritmický dekrement tlmeného harmonického pohybu hmotného bodu je d = 0,03. Vypočítajte, akú časť mechanickej energie stratí hmotný bod za 20 s trvania pohybu, keď perióda tlmeného pohybu je
T = 2 s.

Riešenie:

Celková mechanická energia na počiatku pohybu je:

.

Keďže pri tlmenom pohybe sa amplitúda s časom mení podľa vzťahu

bude mechanická energia v čase t:

Pre logaritmický dekrement platí: d = b T a hmotný bod stratí za čas t energiu:

Relatívna strata energie:

Hmotný bod za 20 s pohybu stratí 45 % energie.

Príklad 6.1.15

Guľôčka s hustotou r = 2,7.10³ kg.m^–3 a s polomerom r = 1 cm, zavesená na pružine, kmitá vo vzduchu s uhlovou frekvenciou ω_o = 6,28 s^–1, ponorená v oleji s uhlovou frekvenciou ω = 5,32 s^–1. Pohyb guľôčky vo vzduchu môžeme považovať za netlmený harmonický pohyb, v oleji za tlmený harmonický pohyb. Vypočítajte dynamickú viskozitu oleja h a logaritmický dekrement d, keď odpor prostredia je úmerný rýchlosti guľôčky podľa Stokesovho vzťahu: F = 6 phrv.

Riešenie:

Pohybová rovnica guľôčky v oleji má tvar:

Z porovnania s rovnicou 6.1.6.2 pre vlastnú frekvenciu netlmeného pohybu platí:

,

pre koeficient tlmenia:

Zo vzťahu medzi uhlovými frekvenciami a koeficientom tlmenia určíme dynamickú viskozitu oleja:

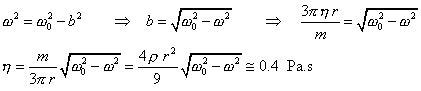
pričom sme dosadili za hmotnosť guľôčky:

.

Logaritmický dekrement vyjadríme z jeho definície:

.