6.1.2 Netlmený harmonický kmitavý pohyb.
Uvažujme sústavu, ktorú tvorí
ideálna pružina na ktorej je upevnené teleso (hmotný bod) hmotnosti m podľa obr. 6.1.1. V tejto časti a aj v
nasledujúcich častiach budeme používať
termín teleso len pre názornosť, pri pohybe sa bude chovať ako hmotný
bod. Budeme predpokladať, že pre deformáciu pružiny (predĺženie, alebo
stlačenie) platí Hookov zákon
a deformácia pružiny je priamo úmerná pôsobiacej sile. Budeme ďalej
predpokladať, že podložka je ideálna a to v tom zmysle, že proti pohybu v
horizontálnom smere nepôsobí žiadna sila trenia.
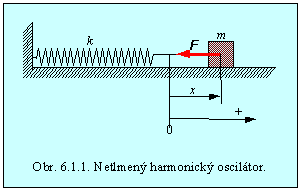
Nech
sa teleso pri nedeformovanej pružine nachádza v počiatku súradnicovej osi . V tejto
polohe na teleso v smere súradnicovej osi nebude pôsobiť žiadna sila a takúto
polohu voláme rovnovážna poloha. Ak ho posunieme o vzdialenosť x, pružinu tým natiahneme a na teleso
bude pôsobiť sila v opačnom smere, ako sme pružinu deformovali. Zložku tejto
sily v smere osi x vyjadruje
rovnica F = – kx, kde k > 0. Takúto silu voláme návratná sila a konštanta k
je silová konštanta
/tiež tuhosť pružiny/. Ak
teleso uvolníme, sila mu udelí zrýchlenie a potenciálna energia natiahnutej pružiny
sa premení na kinetickú energiu telesa. Po prechode rovnovážnou polohou teleso
začne pružinu stláčať. Kinetická energia sa premení na potenciálnu energiu
stlačenej pružiny, situácia sa opakuje a teleso začne vykonávať periodický
pohyb po priamke. Takáto sústava predstavuje lineárny harmonický oscilátor. Ukážeme totiž, že výchylka x z rovnovážnej polohy je harmonickou funkciou času a teda tento
lineárny oscilátor je harmonický.
Pohybová
rovnica pohybu telesa má tvar
![]() (6.1.2.1)
(6.1.2.1)
Prepíšme
ju do tvaru
![]() (6.1.2.2)
(6.1.2.2)
a
zaveďme substitúciu w02= k/m.
Dostávame rovnicu
![]() (6.1.2.3)
(6.1.2.3)
Rovnica
(6.1.2.3) je lineárna diferenciálna rovnica 2. poriadku.
Riešenie rovnice hľadáme v tvare
![]() (6.1.2.4)
(6.1.2.4)
Po
dosadení a úprave dostávame charakteristickú rovnicu
![]() (6.1.2.5)
(6.1.2.5)
z
ktorej vyplývajú komplexne združené korene l1 = iw0 a l2 = –iw0. Z teórie lineárnych diferenciálnych rovníc
vyplýva, že ak rovnici vyhovujú dve riešenia, riešením je aj ich lineárna
kombinácia a všeobecné riešenie pohybovej rovnice pre pohyb za pôsobenia
návratnej sily má tvar
![]() (6.1.2.6)
(6.1.2.6)
Z matematiky vieme, že C1 a C2 sú vo všeobecnosti združené komplexné čísla. Výchylka x je však reálne číslo. Využijeme eij = cosj + i.sinj a zavedieme substitúcie C1+ C2 = A0 cosj, i(C1– C2 ) = –A0 sinj.
Po vykonaní elementárnych úprav dostávame reálny tvar všeobecného riešenia pohybovej rovnice pre harmonický oscilátor
![]() (6.1.2.7)
(6.1.2.7)
kde
x predstavuje okamžitú výchylku v
čase t, A0 je maximálna výchylka alebo aj amplitúda kmitov, argument (w0t + j) je fáza
kmitu a j je fázová konštanta. Fázová konštanta je fáza v čase t = 0. Obidve konštanty A0
a j vyplývajú
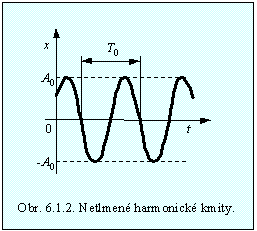
z počiatočných podmienok, ktorými sú obyčajne výchylka a rýchlosť v čase t = 0. Časový priebeh harmonického kmitania
je na obr. 6.1.2.
Nájdime teraz fyzikálny význam konštanty w0.
Zväčšime čas v rovnici (6.1.2.7) o 2p/w0. Dostávame
![]() (6.1.2.8)
(6.1.2.8)
Časový
interval T0 rovný 2p /w0 je
doba, za ktorú sa výchylka opakuje, teda je to perióda kmitov. Platí
![]() (6.1.2.9)
(6.1.2.9)
Frekvencia kmitov f0
je počet kmitov za časovú jednotku
![]() (6.1.2.10)
(6.1.2.10)
odkiaľ
![]() (6.1.2.11)
(6.1.2.11)
Všimnite si, že frekvencia kmitania nijako nezávisí na tom,
ako veľmi sme pružinu natiahli a teda aká veľká je amplitúda kmitov. Závisí len
od hmotnosti kmitajúceho telesa a silovej konštanty pružiny. Veličinu w0
nazývame uhlová frekvencia (tiež kruhová frekvencia) pohybu; jej jednotka v sústave SI je radián za sekundu,
fyzikálny rozmer je s–1.
Riešenie
rovnice (6.1.2.2) môžeme rovnako dobre vyjadriť aj v tvare x
= A0 sin (w0t+j´).
Pri daných počiatočných podmienkach sa pritom len zmení hodnota fázovej konštanty
o p/2.
Vyjadrime teraz rýchlosť a zrýchlenie telesa. Pre rýchlosť
dostávame
![]() (6.1.2.12)
(6.1.2.12)
a
pre zrýchlenie
![]() (6.1.2.13)
(6.1.2.13)
Vidíme,
že rýchlosť predbieha výchylku vo fáze o p/2 a zrýchlenie
predbieha výchylku vo fáze o p.
Uviedli sme už, že konštanty A0 a j pre každý konkrétny prípad harmonického pohybu
môžeme určiť z počiatočných podmienok.
Objasníme si to na nasledujúcom príklade.
______________________________________
Príklad 6.1.1
Vypočítajte amplitúdu a fázovú konštantu
netlmeného harmonického pohybu hmotného bodu po priamke, ak v čase t = 0 s má
okamžitú výchylku xo = x(0) =
0,03 m a rýchlosť vo = v(0) = 0,4 m.s–1
a frekvencia kmitov je f0 = 1 s–1.
Riešenie:
Pre okamžitú výchylku
a rýchlosť v ľubovoľnom čase platí x
= A cos(w0 t + j),
![]()
V čase t = 0 s dostaneme: xo = A0 cos j , vo = – A0 2 pf0 sinj .
Rovnice upravíme do tvaru
![]()
Umocnením a sčítaním rovníc dostávame pre
amplitúdu
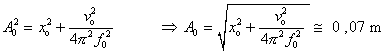 .
.
Vzájomným delením týchto rovníc dostaneme
![]()
Pre fázovú konštantu j platí: j 1 =
115,2° , resp . j 2 = 295,2°.
Príklad 6.1.2
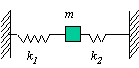
Teleso hmotnosti m je upevnené medzi dvoma pružinami, ktoré majú silové konštanty k1 a k2 a nachádza sa medzi nimi v rovnovážnej polohe.
Vypočítajte periódu kmitov telesa, keď voľné konce pružín sú upevnené podľa
obr. 6.1.3.
Riešenie:
Pri
vychýlení telesa z rovnovážnej polohy budú naň pôsobiť návratné sily F1 = – k1 x , F2 = – k2 x , kde x je výchylka z rovnovážnej polohy. Musíme si
uvedomiť, že smer síl od obidvoch pružín je rovnaký. Ak napríklad teleso
vychýlime z rovnovážnej polohy do prava, pravú pružinu stláčame, ľavú naťahujeme.
Výsledná sila F = – k x
sa rovná súčtu týchto síl.
|
Obr. 6.1.3 |
F = F1 + F 2 = – (k 1+ k2) x , – k x = – (k1+ k2)
x. Odtiaľ pre výslednú silovú
konštantu pružín platí: k = (k1+
k2).
Pre uhlovú frekvenciu kmitavého pohybu
a pre jeho periódu dostaneme:
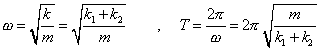 .
.