5.3.3 Povrchové napätie v kvapalinách

Kvapaliny sa snažia zaujímať tvar s minimálnym povrchom. Geometricky je takým útvarom guľa. Má najmenší pomer plochy a objemu. Príčinou tohto javu je povrchové napätie v kvapalinách, ktoré má svoj pôvod v medzimolekulových silách. Uvažujme molekuly nachádzajúce sa v rôznych vzdialenostiach od povrchu. Medzimolekulové príťažlivé sily sú významné iba do určitej vzdialenosti (približne 0,5 nm). Pre každú molekulu teda existuje určitá sféra molekulového pôsobenia.

Ak je molekula pod povrchom hlbšie (obr.5.3.3.1), sily od ostatných molekúl sa kompenzujú, ak je bližšie, alebo celkom na povrchu, výsledkom pôsobenia molekúl kvapaliny je sila smerujúca dovnútra kvapaliny. Táto sila vytvára kohézny tlak. Kohézny tlak nemôžeme priamo merať, jeho hodnoty vyplývajú z termodynamických úvah a sú pomerne vysoké (napr. pre vodu je to 2,03 GPa). Výsledná sila smeruje do vnútra kvapaliny, preto molekuly vo vnútri kvapaliny majú menšiu potenciálnu energiu, ako molekuly na povrchu. Na umiestnenie molekuly na povrch kvapaliny musíme vykonať prácu. S kohéznym tlakom sú spojené veličiny povrchová energia, povrchová sila a povrchové napätie. Povrchová energia je rozdiel vnútornej potenciálnej energie molekuly na povrchu a vo vnútri kvapaliny. Povrchová energia je tým väčšia, čím je väčší povrch. Pre prírastok povrchovej energie platí:

dE = dS (5.3.3.1)

Konštanta je kapilárna konštanta, jej jednotkou je J×m^–2.

Predstavme si rez povrchom kvapaliny. Pre molekuly ležiace na tomto reze je počet na povrchu ležiacich molekúl vo vzdialenosti medzimolekulového pôsobenia na obidvoch stranách rovnaký a celková sila na molekuly nachádzajúce sa na rozhraní je preto nulová. Opačne pôsobiace sily však na povrchu vytvárajú stav napätia. Analogický je stavu, ktorý poznáme pri natiahnutí gumenej blany. Celková sila pôsobiaca na jednu stranu takéhoto mysleného rozhrania je povrchová sila. Táto sila je rovnobežná s povrchom a kolmá na rozhranie. Nech na element dĺžky rozhrania dl kolmo na rozhranie pôsobí povrchová sila veľkosti dF. Táto sila je rovnobežná s povrchom a kolmá na rozhranie. Veličina definovaná vzťahom:

(5.3.3.2)

sa nazýva povrchové napätie. Jednotkou povrchového napätia je N×m^-1.

Definíciu povrchového napätia môžeme objasniť na jednoduchom experimente. Predstavme si rámček s jednou pohyblivou stranou (obr.5.3.3.2).

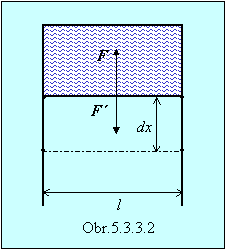
V uzatvorenej časti rámčeka máme kvapalinu, napr. mydlovú blanu. Na pohyblivú časť rámčeka pôsobí sila F = 2s ℓ (povrch je na dvoch stranách blany). Ak pohyblivú stranu rámčeka posunieme o dx, vykoná sa práca dW = Fdx. Táto práca sa súčasne rovná prírastku povrchovej energie, pretože povrch kvapaliny sa zväčší o 2 ℓ dx.

Povrchové napätie je teda totožné s kapilárnou konštantou

Používať preto budeme len jeden symbol s. Jedna z metód na meranie povrchového napätia využíva odkvapkávanie kvapiek z kapiláry. Kvapka na kapiláre polomeru r sa odtrhne, ak povrchová sila na obvode kapiláry sa rovná tiaži kvapky.

––––––––––––––––––––––––––––––––––––––

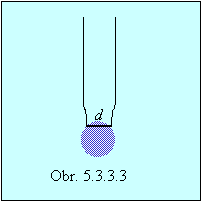
Príklad 5.3.3.1 Vypočítajte povrchové napätie vody s na základe merania priemeru d krčka kvapky, odtrhávajúcej sa od kapiláry (obr.5.3.3.3). Pri meraní sa zistilo, že hmotnosť 318 kvapiek vody bola 5 g a aritmetický priemer hodnoty d krčka bol 0,7 mm.

Riešenie: Pri odtrhnutí kvapky musí platiť, že tiažová sila kvapky prekoná silu povrchového napätia, ktorá drží kvapku na obvode kapiláry: m g = s p d , pričom hmotnosť kvapky

Pre povrchové napätie dostaneme:

Poznámka: Katóda pri polarografii je vytvorená kvapkou ortuti na kapiláre. Odtrhávajúce sa kvapky vytvárajú stále sa obnovujúci povrch katódy. Polomer kvapky je jeden z parametrov vystupujúcich pri odvodení Ilkovičovej rovnice pre intenzitu nasýteného prúdu.