5.3.1 Vnútorné trenie v kvapalinách. Viskozita

Ideálna kvapalina, t.j. kvapalina bez vnútorného trenia je fyzikálna abstrakcia. V reálnych kvapalinách aj v plynoch pozorujeme vnútorné trenie. Jedným z jeho prejavov je, že prúdenie sa zastaví, ak prestanú pôsobiť sily, ktoré ho vyvolali. Z bežného pozorovania vody v koryte rieky vieme, že vrstva vody tesne pri brehu je takmer v pokoji, pričom najväčšia rýchlosť prúdenia je v strede toku. Prúdiacu kvapalinu si môžeme predstaviť zostavenú z navzájom sa pohybujúcich vrstiev (obr.5.3.1.1).

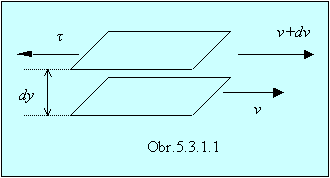
Prúdenie tohto typu je laminárne prúdenie. Vrstvy sa v dôsledku medzimolekulových síl a zrážok molekúl nemôžu pohybovať bez vzájomného ovplyvňovania. Zrážky molekúl a medzimolekulové sily sú príčinou vnútorného trenia. Trenie spôsobuje, že pomalšia vrstva bude urýchľovaná a rýchlejšia spomaľovaná. Časom sa dosiahne rovnovážny stav, pri ktorom relatívne rýchlosti vrstiev budú konštantné a vytvorí sa gradient rýchlosti. Medzi vrstvami vzniká tangenciálne napätie, ktoré podľa Newtona je úmerné gradientu rýchlosti:

(5.3.1.1)

Koeficient úmernosti h nazývame dynamická viskozita. Jednotka dynamickej viskozity je
Pa.s. Je to dynamická viskozita laminárne prúdiacej kvapaliny, v ktorej pri gradiente rýchlosti 1 s^–1 kolmo na smer prúdenia kvapaliny vzniká tangenciálne napätie 1 N×m^–2. Prevrátená hodnota dynamickej viskozity je tekutosť (fluidita):

j = 1/h (5.3.1.2)

Podiel dynamickej viskozity a hustoty r je kinematická viskozita:

(5.3.1.3)

Jednotkou kinematickej viskozity je m²×s^–1. Je to kinematická viskozita kvapaliny hustoty
1 kg×m^–3, ktorej dynamická viskozita je 1 Pa×s. Rovnica (5.3.1.1) platí pre väčšinu kvapalín. Neplatí v koloidných roztokoch, suspenziách, emulziách a pod. Takéto kvapaliny sa nazývajú nenewtonovské.

Koeficient viskozity rastie s tlakom a výrazne tiež závisí na teplote. Pri kvapalinách s teplotou klesá, pri plynoch s teplotou rastie. Rozdielny charakter teplotnej závislosti dynamickej viskozity poukazuje na rozdiely v mechanizme vnútorného trenia v kvapalinách a plynoch.

V kvapalinách a plynoch pozorujeme vo všeobecnosti dva druhy prúdenia a to laminárne a turbulentné. Pri laminárnom prúdení vrstvy kvapaliny sa nepremiešavajú, kĺžu po sebe. Pri laminárnom prúdení a konštantnom prietoku je prúdenie stacionárne. Rýchlostný profil pri takomto prúdení je parabolický (pozri rov. (5.3.2.3)). Pri turbulentnom prúdení dochádza k vzájomnému premiešavaniu vrstiev a vzniku vírov – turbulencií. Turbulentné prúdenie je nestacionárne.

Anglický fyzik Reynolds našiel pre charakterizovanie prúdenia bezrozmerné číslo (Reynoldsovo číslo):

(5.3.1.4)

kde r je hustota, v je stredná rýchlosť kvapaliny (cez prierez potrubia) h je dynamická viskozita a d je priemer potrubia. Pri malých hodnotách Re je prúdenie laminárne (približne do 2300) pri vyšších hodnotách je turbulentné. Reynoldsovo číslo sa používa ako kritérium podobnosti pri predpovedi charakteru prúdenia za rozličných podmienok. Charakter prúdenia v potrubiach rôzneho prierezu bude rovnaký, ak každému prúdeniu prislúcha rovnaké Re.

–––––––––––––––––––––––––––––––––––––––

Príklad 5.3.1.1 V potrubí prúdi oxid uhličitý tak, že za pol hodiny prierezom trubice s priemerom d = 2 cm pretečie m = 0,5 kg tohto plynu. Zistite, či ide o laminárne prúdenie a vypočítajte rýchlosť prúdenia.

Riešenie: Pri ustálenom prúdení pre objemový prietok platí:

Odtiaľ pre rýchlosť prúdenia:

Charakter prúdenia posúdime porovnaním Reynoldsovho čísla s jeho kritickou hodnotou Re_k @2300.

Pretože Re < Re_k , prúdenie je laminárne.