5.2.4 Výtok
kvapaliny otvorom malého prierezu
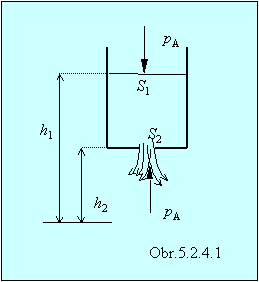
Majme kvapalinu hustoty r v širokej otvorenej
nádobe, na dne ktorej je malý otvor (obr.5.2.4.1).
Tlak v prierezoch S1
aj S2 je rovnaký a rovná
sa atmosférickému tlaku. Bernoulliho rovnica pre miesta 1 a 2 má tvar:
![]() (5.2.4.1)
(5.2.4.1)
Platí S1 >> S2, preto v1
<< v2 a kinetickú energiu objemovej jednotky v mieste 1 môžeme
zanedbať oproti kinetickej energii v mieste 2. Pre rýchlosť výtoku kvapaliny
dostávame:
![]() (5.2.4.2)
(5.2.4.2)
Rozdiel h1 – h2 = h je výška kvapaliny nad otvorom. Vzťah, ktorý sme odvodili pre
rýchlosť výtoku ideálnej kvapaliny otvorom malého prierezu
![]()
sa volá Toricelliho vzťah.
Poznámka: Všimnite si, že
rýchlosť výtoku ideálnej kvapaliny je taká istá, ako by bola rýchlosť telesa
padajúceho z rovnakej výšky. Rýchlosť výtoku reálnych kvapalín bude v dôsledku
viskozity menšia.
Príklad 5.2.4.1 Nádoba postavená na vodorovnej rovine je naplnená
vodou do výšky h = 0,4 m a udržuje sa na tejto hladine. Ako vysoko nad dnom musíme urobiť v
stene nádoby otvor, aby voda striekala čo najďalej na vodorovnú rovinu?
(obr.5.2.4.2)
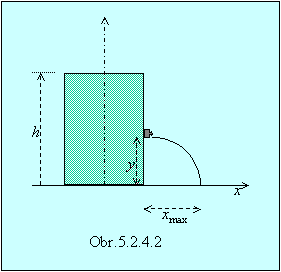
Riešenie: Pre jednotlivé
častice kvapaliny pri vytekaní z otvoru platia kinematické rovnice opisujúce
vodorovný vrh:
![]()
pričom pre výtokovú rýchlosť platí Torricelliho vzťah:
![]() .
.
Po dosadení rýchlosti v a času t, pre súradnicu x dostaneme:
![]()
Hľadáme extrém tejto funkcie, teda:
![]()
Príklad 5.2.4.2 Valcový
rezervoár na vodu s polomerom R = 50
cm má na dne otvor s priemerom d = 4 cm. Do nádoby priteká voda s
objemovým tokom Qp = 0,7×10–2
m3×s–1.
Akú maximálnu výšku dosiahne voda v rezervoári? Ako dlho bude trvať jeho vyprázdnenie, ak
sa prítok vody zastaví v čase, keď hladina vody je maximálna?
Riešenie: Ustálenú maximálnu výšku vody v rezervoári
dostaneme, ak sa prítok vody Qp
rovná výtoku Qv:
![]()
pričom sme za výtokovú rýchlosť dosadili
Torricelliho vzťah.
Po uzavretí prítoku bude sa výtok rovnať časovému
úbytku objemu vody z rezervoára:
![]()
kde V = SV h = p R2 h , pričom
![]() .
.
Po dosadení dostaneme:
![]() .
.
Separáciou premenných a integráciou:
![]()
Kontrolné otázky k časti 5.2
1.
Čo je to objemový a čo hmotnostný prietok?
2.
Čo tvrdí rovnica kontinuity? Platí aj pre plyny?
3.
Čo je to hydrodynamický paradox?
4.
Vyslovte Bernoulliho rovnicu. Aký je význam jej členov?
5.
Odvoďte rozmer každého člena v Bernoulliho rovnici,
6.
Napíšte zákon zachovania energie pre ideálnu tekutinu prúdiacu
vodorovným potrubím.
7.
Aký je rozdiel medzi dynamickou a kinematickou viskozitou?
8.
Aký je rozdiel medzi rýchlostným profilom pri laminárnom
a turbulentnom prúdení?
9.
Napíšte zákon zachovania hmotnosti pre kvapalinu, ktorá prúdi potrubím
s rôznymi prierezmi.
10.
Z akého dôvodu sa kovový nadstavec polievacej hadice na konci zužuje?
11.
Prečo sa prúd kvapaliny vytekajúcej zo dna nádoby zužuje?
12.
Polomer aorty je » 1 cm a krv sa v nej pohybuje rýchlosťou » 30 cm×s–1. Vypočítajte rýchlosť krvi v kapilárach,
ak celková plocha prierezov kapilár je 2000 cm2 (každá kapilára má priemer » 8×10–4 cm, ale sú ich
miliardy).
13.
Pomocou hadice s valcovým nadstavcom máte naplniť vodou bazén známeho objemu.
Viete odhadnúť čas nato potrebný, ak máte k dispozícii iba meter na meranie
dĺžky?
14.
Z trubice ponorenej do vody čerpáme vzduch, pričom hladina vody stúpne
nad vypúšťací kohútik. Bude kohútikom vytekať voda, keď ho otvoríme? (obr.
5.2.1)
15.
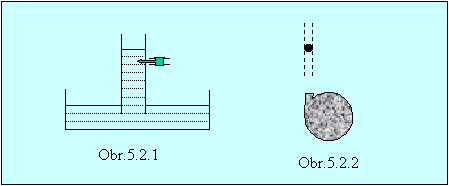
Pri umiestnení
stolnotenisovej loptičky do prúdu vzduchu od ventilátora sa bude loptička
vznášať (obr. 5.2.2). Prečo?
16.
V podpalubí lode vznikol otvor, cez ktorý vteká do lode voda.
Vysvetlite, prečo na priloženie dosky k otvoru je potrebná oveľa väčšia sila
ako potom na jej pridržiavanie na otvore.
17.
Akú počiatočnú rýchlosť má vytekajúca voda z otvoru, ktorý sa nachádza
na dne vodnej nádrže, keď je nádrž naplnená vodou do výšky 4,6 m?
18.
Vysvetlite, prečo kondenzované
mlieko z konzervy vyteká oveľa lepšie, keď urobíte v konzerve dva
otvory, a to na protiľahlých podstavách konzervy.
19.
Voda v ústrednom kúrení prúdi tak, že na
prízemí vstupuje do rúrky s priemerom 4 cm s rýchlosťou 0,5 m.s–1
pod tlakom 3.105 Pa. Aká bude jej rýchlosť a tlak v rúrke s priemerom 2,6 cm na druhom poschodí, ktoré
sa nachádza o 5 m vyššie?
20.
Vysvetlite na základe Bernoulliho rovnice hydrodynamický paradox, teda
zmenšenie tlaku s rastúcou rýchlosťou prúdenia kvapaliny.
21.
Vysvetlite princíp činnosti vodnej vývevy a mechanického rozprašovača!
22.
Do každej ruky vezmite hárok papiera a držte ich zvislo niekoľko
centimetrov od seba. Čo sa stane ak budete do priestoru medzi nimi fúkať,
opíšte a vysvetlite pohyb papierov.
23.
Keď vás predbieha veľkou rýchlosťou idúce auto, alebo keď stojíte na
nástupišti a prechádza okolo vás vlak s
veľkou rýchlosťou, v obidvoch prípadoch vás to priťahuje k rýchlo sa
pohybujúcemu dopravnému prostriedku.
Vysvetlite prečo!
24.
Dve lode plaviace sa na mori blízo vedľa seba rovnakým smerom sa môžu
ľahko zraziť. Vysvetlite, prečo?
25.
Trubicou, ktorá má zúženú časť, preteká voda so vzduchovými bublinkami.
V ktorej časti trubice budú mať bublinky väčší priemer a prečo?
Úlohy k časti 5.2
1. V bočnej stene nádoby, ležiacej na stole, sa nachádza malý otvor vo výške h1 odo dna nádoby a vo vzdialenosti h2 pod hladinou vody, ktorá sa udržiava na konštantnej výške. Do akej vzdialenosti od steny nádoby strieka voda, ak: a) h1 = 25 cm, h2 = 16 cm,
b) h1 =16 cm, h2 = 25 cm? (a) 40 cm; b) 40 cm)
2. Valcová nádoba má v stene nad sebou dva otvory vo výškach h1, h2 odo dna. V akej výške musí byť udržiavaná hladina tekutiny nad dnom nádoby, aby striekala z obidvoch otvorov do rovnakej vzdialenosti na vodorovnú rovinu, na ktorej nádoba stojí? (h = h1+h2)
3. Aký musí byť polomer vzduchovodu kúrenia, aby sa vzduch v izbe objemu 300 m3 úplne obnovoval každých 15 minút? Rýchlosť pohybu vzduchu vo vzduchovode je 3 m×s–1 a hustota vzduchu je konštantná. (18,8 cm)
4. Ako dlho bude trvať naplnenie bazénu vodou, ak rozmery bazénu sú (10 x 20 x 3) m3? Voda priteká hadicou priemeru 2 cm a rýchlosťou 3 m×s–1. (176,8 h)
5. Na dne valcovej nádoby je otvor priemeru d = 2 cm. Do nádoby priteká voda s objemovým tokom Q = 2 ℓ×s–1. V akej výške sa ustáli hladina vody a aký je tlak na dno nádoby? (2,1 m; 2×104Pa)
6.
V horizontálnom potrubí prúdi kvapalina.
Keď do potrubia zhora umiestnime trubicu zalomenú do pravého uhla a priamu
trubicu rovnakého prierezu, rozdiel hladín v týchto trubiciach bude Dh =
10 cm. Určte rýchlosť prúdenia kvapaliny v potrubí! (1,4 m×s-1)
7. Nosné krídlo v aerodynamickom tuneli je
vystavené vzdušnému prúdu rýchlosti
v1 = 40 m×s–1. V
jednom mieste krídla bol nameraný podtlak 2942 Pa. Aká je rýchlosť v2 vzduchu v tomto mieste? (78,5 m×s-1)
8. Aký výkon vyvíja ľudské srdce, keď pri každom údere ľavá predsieň vytlačí do aorty 70 g krvi pod tlakom p = 26 kPa? Tep je 75 úderov za minútu. (2,17 W)
9. Vodorovne uložená injekčná striekačka má priemer piesta D = 1 cm a priemer výtokového otvoru d = 1 mm. Akou rýchlosťou a ako dlho bude otvorom vytekať voda ak objem striekačky je 20 ml a sila pôsobiaca na piest je F = 2 N? (7,1 m×s-1; 3,6 s)
10. Vodorovným potrubím prúdi rovnomerne voda. Tlak v potrubí je 3.104 Pa, priemer potrubia je D = 0,5 m. Tlaky v hlavnom potrubí a v zúženej časti sa líšia o Dp = 1.104 Pa. Aký je priemer, rýchlosť a tlak vody v zúženej časti potrubia, ak prietok je Q = 500 ℓ.s–1? (0,35 m; 5,1 m×s-1; 2×104 Pa)