5.2.3   Bernoulliho rovnica

      

Z rovnice kontinuity vyplýva, že pri prúdení kvapaliny v potrubí meniaceho sa prierezu sa kvapalina pohybuje so zrýchlením. Zväčšovanie rýchlosti prúdenia kvapaliny vo vodorovnej trubici môže spôsobiť len rozdielny tlak. Z tejto jednoduchej úvahy vyplýva, že v miestach s väčšou rýchlosťou kvapaliny musí byť tlak menší.

Pre kvantitatívnu formuláciu týchto zmien budeme skúmať prúdenie ideálnej kvapaliny hustoty r. Zvoľme si v prúdiacej kvapaline dostatočne úzku prúdovú trubicu a sledujme energiu objemového elementu kvapaliny prechádzajúceho najprv miestom 1 a potom 2. (obr.5.2.3.1).  Hmotnostný stred elementu kvapaliny v mieste 1 je o h = h1 – h2 vyššie ako v mieste 2. Ak prierez  S1 je väčší ako S2 podľa rovnice kontinuity musí byť rýchlosť v2 > v1. Prúdová trubica je dostatočne úzka, t.j. rýchlosť môžeme v celom priereze S1 a S2 považovať za konštantnú. Za časový interval  Dt miestom 1 prešiel objem    DV = v1 Dt S1  a častice kvapaliny, ktoré sa nachádzali v priereze S1 sú teraz v priereze . Miestom 2 prešiel taký istý objem, lebo kvapalina je nestlačiteľná  DV  = v2 Dt S2 a častice kvapaliny prešli z prierezu S2 do . Pri stacionárnom prúdení v objeme medzi  a S2 nedochádza k žiadnym zmenám, iba jedny častice sa zamieňajú druhými. Potrebné je preto sledovať iba zmeny medzi  a .

 


 

 


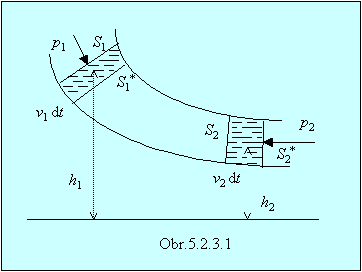
Práca výslednice síl sa rovná prírastku kinetickej energie hmotnostného elementu Dm = r DV.  Prácu koná tlaková sila a gravitačná sila. Tlakové sily pôsobiace z bočných strán prúdovej trubice sa navzájom rušia. Tangenciálne sily nie sú, pretože kvapalina je ideálna a nemá vnútorné trenie. Práce tlakových síl sú  W1 = p1 S1 v1 Dt  a  W2 =  – p2 S2 v2 Dt. Celková práca tlakových síl je Wp = (p1 – p2) DV. Práca gravitačnej síly sa rovná úbytku potenciálnej energie. Ak hmotnostné stredy objemových elementov sú vo výškach h1 a h2 nad vzťažnou rovinou, potom práca gravitačnej sily Wg = r DVg (h1– h2). Platí teda rovnica:

                                                 (5.2.3.1)

Môžeme ju upraviť na tvar:

                                                              (5.2.3.2)

Prierezy S1 a S2 sme volili ľubovoľne, preto výraz

v ktorom prvý člen vyjadruje kinetickú energiu objemovej jednotky, druhý člen potenciálnu energiu objemovej jednotky a p je tlak, musí mať rovnakú hodnotu v ľubovoľnom mieste danej prúdovej trubice. Podľa predpokladov o malosti prierezov S1 a S2  a intervalu Dt rovnica (5.2.3.2) bude platiť tým presnejšie, čím bude prierez prúdovej trubice menší. Rýchlosť, výšku h a tlak na pravej a ľavej strane rovnice (5.2.3.2) budeme preto vzťahovať na určitú prúdovú čiaru. Z odvodenia rovnice a rozmerov jej členov vyplýva jej nasledovná fyzikálna intepretácia:

Pri ustálenom prúdení ideálnej kvapaliny v gravitačnom poli je súčet kinetickej a potenciálnej energie objemovej jednotky a tlaku pozdĺž prúdovej čiary konštantný.

                                                                                   (5.2.3.3)            

Táto rovnica sa volá  Bernoulliho rovnica. (Daniel Bernoulli, 1700 – 1782).   Vyjadruje zákon zachovania mechanickej energie pri ustálenom prúdení ideálnej kvapaliny.

 

Poznámka 1. Konštanta v rovnici (5.2.3.3) je rovnaká pozdĺž určitej prúdovej čiary. Vo všeobecnosti sa môže meniť pri prechode od jednej prúdovej čiary k druhej. Môžeme sa stretnúť s prípadmi, keď je táto konštanta rovnaká pre všetky prúdové čiary. Je to napríklad vtedy, keď všetky prúdové čiary sa začínajú, alebo končia v takej oblasti, kde v = 0.

 

Poznámka 2. O tlaku hovoríme, že je hydrostatický v tých miestach, kde je kvapalina v pokoji. Z Bernoulliho rovnice potom platí  p0 = konšt. – rgh.  V rovnakej výške je pri prúdení kvapaliny hydrodynamický tlak

      

Hydrodynamický tlak je za inak rovnakých podmienok o kinetickú energiu objemovej jednotky menší ako hydrostatický tlak.

 

Poznámka 3. Čím je rýchlosť kvapaliny väčšia, tým je v danom mieste za rovnakých ostatných podmienok tlak menší. Tento fakt, ktorý sa laickému pozorovateľovi zdá nepochopiteľný má názov „hydrodynamický paradox“.

––––––––––––––––––––––––––––––––––––––

Príklad 5.2.3.1 Rozdiel tlakov v hlavnom potrubí a v zúženej časti vodomeru je Dp = 1×105 Pa. Aký je objemový prietok vody vodomerom, ak priečne prierezy hlavného potrubia a zúženej časti sú  S1 = 0,1 m2, S2 = 0,05 m2?

Riešenie: Pre vodorovnú trubicu môžeme písať zjednodušený tvar Bernoulliho rovnice:

Po vyjadrení rýchlosti v2 z rovnice kontinuity:  S1 v 1= S2 v2

a pretože  p1 – p2 = D p,  dostaneme:

    

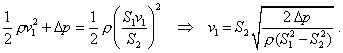
Hľadaný objemový prietok:

 

Príklad 5.2.3.2 Vzdušný prúd obteká krídlo lietadla laminárnym prúdením. Ak rýchlosť vzduchu obtekajúceho spodnú plochu krídla je v1 = 100 m×s–1, akú rýchlosť v2 musí mať vzduch nad hornou plochou krídla, aby vznikol vztlak 1000 Pa?

Riešenie:  Zjednodušene predpokladajme, že pre vzdušný prúd obtekajúci krídlo platí  h1 = h2 Potom má Bernoulliho rovnica tvar:

    

Vztlak  Dp je rozdiel tlakov vzduchu  p1 – p2  pôsobiacich zospodu a zhora na krídlo lietadla. Preto rýchlosť v2 bude:            

 

 

 

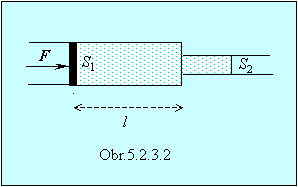
Príklad 5.2.3.3 Injekčná striekačka (obr. 5.2.3.2) dĺžky l = 4 cm má prierez piesta  S1 = 120 mm2  a otvor ihly má prierez S2 = 1 mm2. Ako dlho bude vytekať kvapalina hustoty r = 1050 kg×m–3 zo striekačky, ak je uložená vo vodorovnej rovine a na piest pôsobíme silou F = 5 N?

 


 


Riešenie: Bernoulliho rovnica bude mať tvar :

 

Pre rýchlosť v2 z rovnice kontinuity platí: 

Po dosadení do predošlej rovnice a úprave, dostaneme pre rýchlosť pohybu piesta v1:

 

  

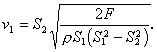
Pri rovnomernom pohybe piesta bude čas vytekania: