5.2.2 Rovnica kontinuity

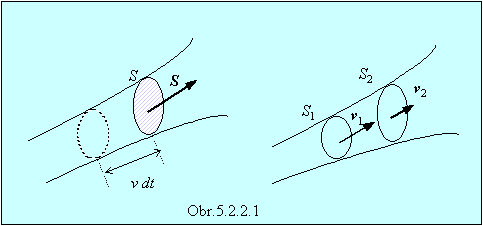
Majme prúdovú trubicu, ktorej prierez kolmý na smer rýchlosti je S. Predpokladajme, že rýchlosť častíc kvapaliny vo všetkých bodoch tohto prierezu je rovnaká. Za časový interval Dt cez prierez trubice prejdú všetky častice, ktorých vzdialenosť od tohto prierezu nebola väčšia ako v Dt. Za interval Dt cez S pretečie hmotnosť kvapaliny r S v Dt a za časovú jednotku teda hmotnosť r S v (hmotnostný prietok) a objem S v (objemový prietok). Ak je prúdenie stacionárne, potom taká istá hmotnosť kvapaliny ako prierezom S₁ musí prechádzať prierezom S₂ (obr.5.2.2.1).

Zákon zachovania hmotnosti pri stacionárnom prúdení potom vyjadruje rovnica:

(5.2.2.1)

Ak hustota kvapaliny je konštantná, teda r₁ = r₂ , potom platí:

(5.2.2.2)

a objem pretečený za časovú jednotku prierezom S₁ sa musí rovnať objemu pretečenému prierezom S₂ (cez plášť trubice kvapalina neprechádza). Pre nestlačiteľnú kvapalinu potom v ktoromkoľvek priereze platí:

S v = konšt. (5.2.2.3)

Túto rovnicu nazývame rovnica kontinuity pre nestlačiteľné kvapaliny. Objem kvapaliny, ktorý pretečie prierezom prúdovej trubice, alebo potrubia za časovú jednotku nazývame objemový prietok, alebo jednoducho prietok Q. Ak je rýchlosť prúdenia v každom bode uvažovaného prierezu rovnaká, prietok Q = S v. V prípade, že v uvažovanom priereze rýchlosť nie je rovnaká, potom prietok je určený vzťahom