5.1.4 Archimedova
sila
Dôsledkom
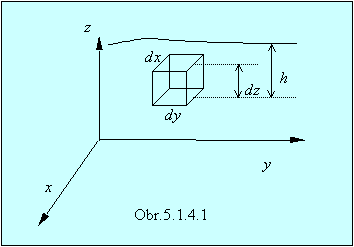
hydrostatického tlaku je Archimedova vztlaková sila. Majme v kvapaline hustoty r
úplne ponorené teleso rozmerov dx, dy, dz
(obr.5.1.4.1).
Hydrostatický tlak je iba
funkciou súradnice z, v dôsledku čoho
sa rušia zložky tlakových síl pôsobiacich na element dV v smere osí x a y. Zložka tlakových síl v smere osi z sa rovná rozdielu tlakových síl
pôsobiacich na dolnú a hornú základňu:
![]()
Na teleso objemu dV bude pôsobiť smerom nahor sila, ktorej
veľkosť sa rovná tiaži kvapaliny telesom vytlačenej.
Archimedov
zákon:
Teleso
je nadľahčované silou, ktorá sa rovná tiaži telesom vytlačenej kvapaliny.
––––––––––––––––––––––––––––––––––––––
Príklad 5.1.4.1 Vážením
sme zistili, že hmotnosť koruny na vzduchu je 1,47 kg. Keď korunu celú ponoríme
do vody, zistíme, že jej „zdanlivá“ hmotnosť
je 1,34 kg. Zistite, či je koruna zhotovená zo zlata!
Riešenie: Hustota koruny s
hmotnosťou mk a objemom Vk je
![]()
Ak ju úplne ponoríme do vody, bude na ňu
pôsobiť výsledná sila (zdanlivá tiaž) vo vode:
F = G – Fv , kde
G = mk g
je tiažová sila na vzduchu, vztlaková sila
![]()
![]()
- je objem vytlačenej vody. Ak je teleso
úplne ponorené, platí
![]()
Potom:
![]()
Odtiaľ pre hustotu koruny dostaneme:
![]()
Keďže
![]()
koruna nie je vyrobená zo zlata, ale podľa
tabuliek je olovená.
Príklad 5.1.4.2 V mori pláva ľadová
kryha. Vypočítajte celkový objem kryhy, keď nad vodu vyčnievajúca časť kryhy má
objem V1 = 180 m3.
Riešenie: Celkový objem kryhy je V = V1 + V2 kde V2 je
objem ponorenej časti kryhy. Ak kryha pláva na povrchu, musí platiť rovnováha
síl: G + Fv = 0 ,
pričom tiažová sila G = mľ g = rľ V g = rľ (V1 + V2) g , vztlaková sila
![]()
Za rovnováhy sa budú veľkosti síl rovnať
(smery sú opačné):
![]()
pričom sme dosadili z tabuliek hustotu morskej vody a hustotu ľadu:
![]()
Príklad 5.1.4.3 Keď do valcovej
nádoby s vodou položíme na jej hladinu zhora otvorenú železnú škatuľku, hladina
vody v nádobe sa zvýši o ℓ = 2 cm. O koľko sa zníži hladina
keď škatuľku potopíme?
Riešenie: Ak škatuľka pláva na povrchu vytlačí časť
vody s objemom
![]()
rovným objemu ponorenej časti škatuľky, kde S je prierez dna nádoby, ℓ – výška zdvihnutia hladiny vody.
Musí platiť rovnováha síl G = FV
, teda:
![]()
Ak
je škatuľka ponorená celá, objem vytlačenej vody je rovnaký ako celý objem
materiálu škatuľky. Hladina sa zdvihne o výšku
x :
![]()
Zníženie hladiny
![]()
Kontrolné otázky k časti 5.1
1.
Aký je rozdiel
medzi kvapalinou a plynom?
2.
Aký je rozdiel medzi tuhou látkou a kvapalinou?
3.
Čo rozumiete pod ideálnou kvapalinou?
4.
Zostane kvapalina v pokoji, ak sa v nej vyskytne tangenciálne
napätie?
5.
Čo je príčinou hydrostatického tlaku?
6.
Hydrostatický tlak môžeme interpretovať ako vplyv .... objemu?,
hmotnosti?, tiaže? ...správnu odpoveď zdôvodnite!
7.
Dokážte, že jednotkou tlaku je podiel jednotky energie a jednotky
objemu!
8.
Predpokladajte, že na kvapalinu, ktorá je v pokoji okrem tiaže pôsobí
ešte iná sila. Ako sa zmení hladina kvapaliny?
9.
Čo tvrdí Pascalov zákon?
10. Prečo pri presnom vážení
robíme korekciu na vákuum?
11.
Pritlačte na ruku ceruzku s tupým koncom a ihlu. Ak pôsobíte rovnako
veľkou silou v obidvoch prípadoch, prečo sa ihlou skôr poraníte?
12. Akou silou pôsobí atmosféra na
dosku stola rozmerov 2 m x 1 m a to: a) zhora, b) zospodu
stola?
13. Ako
určíte hustotu svojho tela, ak nepoznáte jeho objem, ale máte k dispozícii váhy
a bazén s vodou?
14.
Prečo sa v morskej vode ľahšie udržíte na povrchu ako v bazéne?
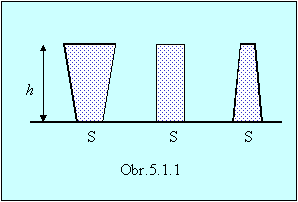
15.
Tri rôzne nádoby ale s rovnakou plochou dna sú naplnené vodou do
rovnakej výšky. Aký bude tlak vody na dno každej nádoby? Aké budú hmotnosti
vody v jednotlivých nádobách? (obr. 5.1.1)
16.
Loď naplnená kameňmi nemôže prejsť pod nízkym mostom. Čo musíme urobiť - vyložiť časť nákladu alebo
naopak loď viac zaťažiť, aby pod mostom preplávala?
17.
Kocka ľadu pláva v pohári naplnenom po okraj vodou. Preleje sa voda, ak
sa ľad roztopí?
18.
Na povrchu vody vo vedre pláva prázdny medený hrnček. Zmení sa hladina
vody vo vedre, ak hrnček potopíme?
19.
Prečo poleno tvaru valca s hustotou 600 kg m–3 nikdy nebude
plávať na vode vertikálne, ale bude plávať horizontálne?
20.
Na koncoch rovnoramennej páky sú zavesené dve rovnaké závažia. Čo sa
stane ak jedno ponoríme do vody a druhé do oleja?
21.
Na rovnoramenných váhach v rovnovážnom stave sa nachádza mosadzná a
sklená guľka. Poruší sa rovnováha a ako, keď váhu premiestnime do vákua, resp.
ponoríme do vody?
22.
Pri vážení akého materiálu na rovnoramených váhach netreba ani pri
najpresnejších meraniach brať do úvahy vztlak vzduchu?
23.
Teleso vo vode váži trikrát menej ako vo vzduchu. Aká je hustota
telesa?
24.
Na dne jazera leží kameň s
hmotnosťou 70 kg a s objemom 3.104 cm3. Aká sila je
potrebná, aby sme ho zodvihli z dna?
25.
Aký musí byť objem hélia, aby balón ním naplnený zodvihol hmotnosť 800
kg?
26.
Hladina vody vo vodojeme je o 30 m
vyššie ako vodovodný kohútik. Aký je tlak vody v kohútiku?
27.
Aký je rozdiel tlaku krvi na úrovni hlavy a chodidiel človeka vysokého
1,7 m?
28.
Akú prvú pomoc z hľadiska hydromechaniky poskytneme človeku pri
odpadnutí - nedokrvení mozgu?
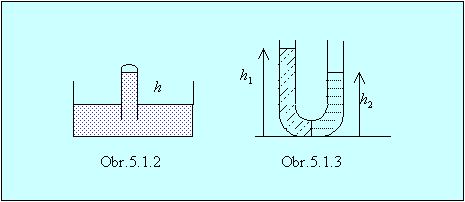
29.
Do akej výšky vystúpi ortuť v ortuťovom manometri so zataveným koncom
pri meraní atmosférického tlaku ? (obr.5.1.2)
30.
Jedno rameno U-trubice je zaplnené liehom, druhé kvapalinou
nemiešajúcou sa s liehom, ktorá má hustotu 990 kg m–3 (obr.5.1.3).
Ak sa rozhranie týchto kvapalín nachádza v dolnom ohybe a výška stĺpca liehu je
18 cm, akú výšku bude mať stĺpec kvapaliny?
Úlohy k časti 5.1
5.1.1 Aká tlaková sila pôsobí na výpustný ventil, ktorého plocha je 1,2 cm2, keď výška vody v cisterne je 2,5 m? (2.9 N)
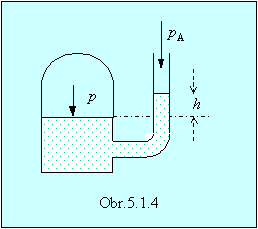
5.1.2 V bočnej stene uzavretej nádoby
naplnenej vodou je upevnená piezometrická trubica. Aký tlak pôsobí na voľný
povrch vody v nádobe, ak účinkom tohto tlaku voda v trubici stúpne o h
= 1,5 m nad hladinu vody v nádobe? (obr.5.1.4). (1,16×105 Pa)
5.1.3 Určte nadmorskú výšku h miesta, kde bol nameraný tlak p
= 0,5×105 Pa, keď predpokladáme, že teplota vzduchu sa s výškou nemenila. Na úrovni mora je normálny
atmosférický tlak pA. (5611 m)
5.1.4 Aký atmosférický tlak nameria horolezec vo výške h = 5000 m nad hladinou mora, ak teplota vzduchu je konštantná v celej vrstve atmosféry a na hladine mora je normálny atmosférický tlak? (5,4×104 Pa)
5.1.5 Vypočítajte hĺbku vody, do ktorej treba ponoriť
vzduchovú pištoľ kalibru d = 7 mm, aby po stisnutí kohútika
nevyšiel výstrel. Hlaveň pištole má dĺžku l
= 0,22 m, hmotnosť guľky m = 7 g
a jej rýchlosť pri opustení hlavne pri výstrele vo vzduchu je v = 27 m×s–1.
(30,8 m)
5.1.6 Malý piest hydraulického lisu sa posúva o h1 = 0,2 m, zatiaľčo veľký piest o h2 = 0,01 m. Akú silu vyvinie lis, keď na malý piest pôsobíme silou F1 = 500 N? (10 kN)
5.1.7 Akou veľkou silou pôsobí voda na bočnú obdĺžnikovú
stenu nádoby, keď vodorovná dĺžka steny a
= 0,2 m a zvislá b = 0,15 m a keď
nádoba je celkom naplnená vodou?
(22 N)
5.1.8 Vypočítajte veľkosť sily pôsobiacej na bočnú stenu a veľkosť sily na dno uzavretej expanznej nádoby tvaru kocky s hranou a = 30 cm, ktorá je naplnená kvapalinou s hustotou r = 780 kg m–3. Manometer pripojený tenkou trubicou k vrchnej stene ukazuje pretlak Dp = 1×104 Pa. (1,1 kN; 1 kN)
5.1.9 Na piest injekčnej striekačky pôsobíme silou 3N. Ak je priemer piesta 1 cm a priemer kanála ihly 0,2 mm, vypočítajte: a) akú silu kvapalina prekonáva pri vytekaní z ihly, b) akou silou musíme pôsobiť na piest striekačky, aby sme zaviedli kvapalinu do žily, v ktorej je pretlak 2394 Pa? (1,2×10-3 N; 1,88×10-1 N)
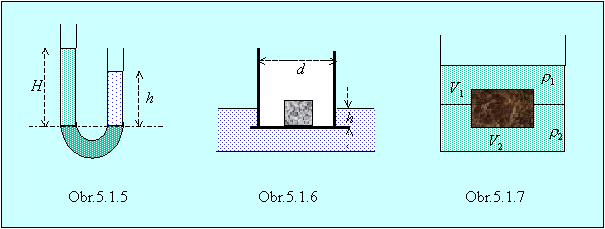
5.1.10 Do trubice tvaru U je naliata ortuť (obr.5.1.5). Do
jedného ramena je potom naliata voda a do druhého olej s hustotou r = 900 kg m–3 tak, aby výška hladiny ortuti v obidvoch
ramenách bola rovnaká. Určte výšku vodného
stĺpca h, keď výška olejového stĺpca H = 20 cm. (18 cm)
5.1.11 Sklená trubica s priemerom d = 5 cm, ktorej dolný koniec je uzavretý platničkou (obr.5.1.6), je ponorená vertikálne do vody, do hĺbky h = 80 cm. Ako veľké závažie môžeme položiť v trubici na platničku tak, aby neodpadla? (1,57 kg)
5.1.12 Aká je hmotnosť lode, ktorá má plochu prierezu na úrovni ponoru S = 1200 m2, ak pri prechode z rieky do mora sa ponor zmenší o h = 0,15 m? (6,87×106 kg)
5.1.13 Aerometer sa ponorí vo vode do hĺbky ho, v kvapaline s hustotou r1 do hĺbky h1. Ako hlboko sa ponorí v kvapaline hustoty r ?
![]()
5.1.14 Na rozhraní dvoch
nemiešajúcich sa kvapalín, ktorými sú voda a ortuť pláva kocka z materiálu
hustoty
r = 11,3×10 3 kg m–3. Aká
časť objemu kocky sa nachádza v hornej kvapaline? (obr.5.1.7) (0,18 V)
5.1.15 Kus ľadu s hmotnosťou m = 1,9 kg pláva na celom povrchu valcovej nádoby naplnenej kvapalinou s hustotou r = 950 kg×m–3. Ako sa zmení výška hladiny, ak sa všetok ľad roztopí (pričom voda a daná kvapalina sa nemiešajú), ak prierez dna nádoby je S = 40 cm2? Ako sa zmení výška hladiny, ak ľad pláva na vode teploty 0 °C a roztopí sa? (zníži sa o 0,025 m; nezmení sa)
5.1.16 Dutá hliníková guľôčka s hmotnosťou m = 0,5 kg je ponorená polovicou svojho objemu do oleja hustoty r = 800 kg×m–3. Aká je hrúbka steny guľôčky a jej priemer? (3,5 mm; 13,36 cm)
5.1.17Aká je hustota
skúmanej kvapaliny, ak tiaž telesa ponoreného do tejto kvapaliny je 0,65 N,
tiaž toho istého telesa ponoreného do vody je 0,64 N a jeho tiaž na vzduchu je
0,69 N? (800 kg×m-3)
5.1.18 Kúsok skla má tiaž 1,37 N. Ak je ponorené do vody jeho tiaž je 0,824 N. Aká je hustota skla? (2504 kg×m-3)
5.1.19 Kus železa má vo vode tiaž 1,67 N. Aký je jeho objem? (24,6 cm3)
5.1.20 Tiaž bronzovej sošky na vzduchu je 21,1 N a vo vode 11,3 N. Aký je objem vzduchovej dutiny v soške? (755 cm3)
5.1.21 Dutá mosadzná guľa má vonkajší priemer 10 cm a hrúbku steny 0,3 cm. Zistite, či táto guľa bude plávať na vode, alebo či klesne na dno nádoby! (klesne)
Tabuľka hustôt a dynamických viskozít niektorých látok
|
Látka |
Hustota r |
Dynamická viskozita h (Pa.s) |
Látka |
Hustota r (103
kg.m–3) |
|
Hélium |
0,18 |
1,87.10–5 |
Hliník |
2,7 |
|
Vzduch |
1,29 |
1,8.10–5 |
Železo |
7,9 |
|
Oxid uhličitý |
1,976 |
1,37.10–5 |
Nikel |
8,9 |
|
Lieh |
790 |
|
Olovo |
11,3 |
|
Ľudská krv (37 °C) |
1,05.103 |
4.10–3 |
Ortuť |
13,6 |
|
Voda (0 °C) |
999,843 |
1,79.10–3 |
Zlato |
19,3 |
|
Voda (4°C) |
999,975 |
1,51.10–3 |
Oceľ |
7,7 |
|
Voda (20°C) |
998,206 |
1,00.10–3 |
Mosadz |
8,5 |
|
Morská voda |
1025 |
|
Bronz |
8,8 |
|
Ľad |
916,8 |
|
Sklo |
3,5 |
|
Olej transformátorový |
866 |
3,16.10–2 |
|
|
|
Olej terpentínový |
855 |
1,49.10–3 |
|
|
|
Olej ricínový |
960 |
9,87.10–1 |
|
|
|
Olej minerálny |
900 |
|
|
|
Atmosférický
tlak za normálnych podmienok pA = 1, 01325 . 10 5 Pa.