5.1.1 Základná rovnica hydrostatiky

Uvažujme kvapalinu, ktorá je v pokoji. Ako vyplýva z úvahy uvedenej v úvode, kvapalina nemôže odolávať tangenciálnemu napätiu a z plošných síl na element kvapaliny, ktorá je v pokoji, môže pôsobiť iba normálové napätie – tlak. Objemovú silu pôsobiacu na určitý element kvapaliny charakterizuje objemová hustota sily f. Predstavme si v kvapaline plochu, ktorá uzatvára objem V. Ak je kvapalina obsiahnutá v tejto ploche v rovnováhe, potom sa súčet všetkých plošných síl pôsobiacich cez rozhranie na danú kvapalinu a objemových síl pôsobiacich na touto plochou uzatvorený objem kvapaliny musí rovnať nule. Rovnováhu plošných a objemových síl vyjadruje v integrálnom tvare rovnica:

(5.1.1.1)

Pripomíname, že vektor elementu plochy dS je definovaný tak, že smeruje z uzatvorenej plochy von. Tlaková sila na element plochy je preto – pdS.

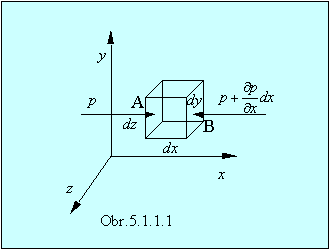
Hľadáme teraz rovnicu, ktorá bude vyjadrovať podmienku rovnováhy síl v diferenciálnom tvare, teda pre každý bod kvapaliny. Majme nekonečne malý objemový element dV = dx dy dz

umiestnený v pravouhlej súradnicovej sústave podľa obr.5.1.1.1. Tlak je iba funkciou polohy, nie orientácie plochy, a ak sa v bode A (x, y, z) rovná p, potom v bode B (x + dx, y, z) sa rovná:

(5.1.1.2)

V smere osi x pôsobí tlak na dve steny objemového elementu. Podmienku rovnováhy objemových a plošných síl v osi x vyjadríme rovnicou:

(5.1.1.3)

ktorá po úprave nadobúda tvar:

(5.1.1.4a)

Analogicky dostaneme rovnice vyjadrujúce podmienky rovnováhy v smere osí y a z:

(5.1.1.4b,c)

Po vynásobení týchto rovníc jednotkovými vektormi i, j, k a sčítaní dostávame vo vektorovom tvare základnú rovnicu hydrostatiky:

(5.1.1.5)

kde gradient tlaku je vektor

Objemová hustota sily v kvapaline, ktorá je v pokoji, sa rovná gradientu tlaku. Objemovú hustotu sily môžeme vyjadriť pomocou hustoty kvapaliny a intenzity príslušného vonkajšieho poľa vzťahom f = r E.

V prípade, že silové pole objemových síl je konzervatívne, t.j. pre intenzitu platí E = – grad j , kde j je potenciál príslušného poľa, dostávame všeobecne platnú rovnicu hydrostatiky:

(5.1.1.6)

Ak hustota r je konštantná, potom

a rovnicu (5.1.1.6) môžeme vyjadriť v tvare

odkiaľ vyplýva:

(5.1.1.7)

Fyzikálna interpretácia tejto rovnice je: súčet potenciálnej energie objemovej jednotky a tlaku pre nestlačiteľnú kvapalinu v konzervatívnom silovom poli je konštantný.

V gravitačnom poli s konštantnou intenzitou platí pre potenciál gravitačného poľa: j = gh, kde g je gravitačné zrýchlenie a h je výška nad zvolenou hladinou nulového potenciálu. Rovnicu hydrostatiky pre nestlačiteľnú kvapalinu v gravitačnom poli dostávame potom v tvare:

(5.1.1.8a)

–––––––––––––––––––––––––––––––––––––

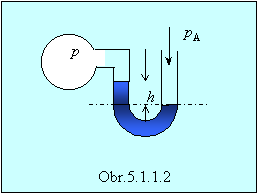
Príklad 5.1.1.1 Na určenie tlaku v nádobe naplnenej plynom použijeme otvorený ortuťový vákuomer (obr.5.1.1.2). Aký je tlak plynu v nádobe, ak rozdiel hladín ortuti v trubiciach vákuomera je h = 0,45 m?

Riešenie: Rozhranie ortuť-vzduch si zvolíme za vzťažnú rovinu. Potom zo základnej rovnice hydrostatiky platí

Hľadaný tlak bude:

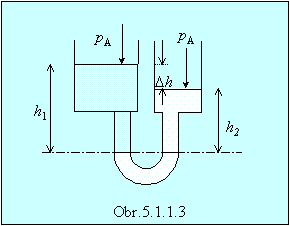
Príklad 5.1.1.2 Dve otvorené ramená spojených nádob sú naplnené navzájom sa nemiešajúcimi kvapalinami a to vodou a terpentínovým olejom. Aká je vzdialenosť hladín kvapalín v jednotlivých ramenách od spoločného rozhrania (obr. 5.1.1.3), keď rozdiel výšok hladín v ramenách je Dh = 10 cm ?

Riešenie: Zo základnej rovnice hydrostatiky v stave rovnováhy platí r φ + p = konšt., kde φ je potenciál tiaže. Ak spoločné rozhranie kvapalín volíme za vzťažnú rovinu kde φ = 0, musí byť v obidvoch ramenách tlak v kvapaline rovnaký, teda:

r₁ g h₁ + p_A = r ₂g h ₂+ p_A , pričom h₁ – h₂ = Dh.

Z týchto dvoch rovníc úpravou dostaneme:

–––––––––––––––––––––––––––––––––––––

Ak je zmena potenciálnej energie vzhľadom na rôzne miesta v kvapaline oproti tlaku zanedbateľná, potom z tejto rovnice vyplýva známy Pascalov zákon: vo vnútri ako aj na hraničných plochách je v kvapaline, ktorá je v pokoji a nepôsobia na ňu vonkajšie sily, všade rovnaký tlak:

p = konšt. (5.1.1.8b)

Táto skutočnosť sa v praxi využíva v hydraulických lisoch.

–––––––––––––––––––––––––––––––––––––

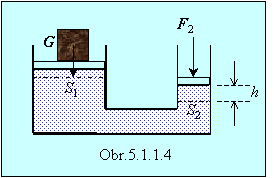
Príklad 5.1.1.3 Pri dvíhaní nákladu hmotnosti m = 2 t pomocou hydraulického zdviháka (obr. 5.1.1.4) sa vykonala práca W = 40 J. Pritom malý piest vykonal 10 zdvihov a pri každom sa posúval o h =10 cm. Koľkokrát je plocha väčšieho piestu S₁ väčšia než plocha malého piestu S₂ ?

Riešenie: Práca pri n-krát opakovanom pohybe malého piesta je: W = n F₂ h. Z Pascalovho zákona o rovnomernom šírení sa tlaku v kvapaline pritom platí:

Odtiaľ platí:

Pre hľadaný pomer prierezov: