1.      Dva voľné hmotné body A a B s hmotnosťami   a  sú v rovnomernom pohybe. V čase  t = 0 je vzdialenosť bodov AB = d. Rýchlosť v2 bodu B má smer spojnice AB a rýchlosť v1 bodu A je na ňu kolmá. Nájdite rovnicu dráhy a rýchlosť ťažiska tejto sústavy hmotných bodov. Aký pohyb vykonáva ťažisko? Riešenie .

Obr.1

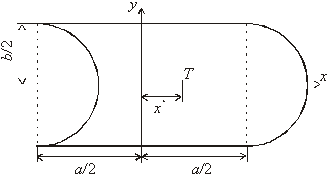
2.      Nájdite polohu ťažiska útvaru znázorneného na obr.1, ktorý vznikol tak, že sa z obdĺžnika so stranami a, b vyrezal na jednej jeho strane  polkruh polomeru b/2 a priložil sa na druhú stranu obdĺžnika! Riešenie .

3.      Vypočítajte moment zotrvačnosti tenkého drôtu hmotnosti m zohnutého do tvaru kružnice polomeru R vzhľadom na os kolmú na rovinu, v ktorej leží kružnica a prechádzajúcu stredom kružnice..

4.      Vypočítajte moment zotrvačnoti homogénnej tyče prierezu S0, dĺžky l   a hmotnosti  m  vzhľadom na os kolmú na dĺžku tyče a prechádzajúcu   a) koncovým bodom tyče, b) ťažiskom tyče ! Riešenie .

5.      Vypočítajte moment zotrvačnosti homogénneho plného valca hmotnosti  m , polomeru R, výšky h  vzhľadom na rotačnú os totožnú s jeho osou symetrie. Zvážte, od čoho nezávisí.

J = 

7.      Tenký drôt hmotnosti  m  je zohnutý do tvaru kružnice polomeru  R  a uložený v tiažovom poli na vodorovnú os. Po malom vychýlení z rovnovážnej polohy ho voľne pustíme. Vypočítajte dobu kyvu a redukovanú dĺžku tohto kyvadla !(Riešte pre hodnoty    R=4,9cm, Riešenie .

8.      Zotrvačníkové koleso, ktoré má spolu s hriadeľom moment zotrvačnosti vzhľadom na os otáčania  J, otáča sa tak, že vykonáva  N  otáčok za minútu. V okamihu, keď prestanú pôsobiť vonkajšie sily svojím otáčavým momentom, koleso sa zastaví počas doby tz. Za predpokladu, že trecie sily sú konštantné, vypočítajte ich moment vzhľadom na os  !

(Riešte pre hodnoty   ) Riešenie .

9.      Homogénna kruhová doska je uložená na vodorovnej osi prechádzajúcej jej stredom a kolmej na rovinu dosky. Na  obvode je navinuté lanko,  ktoré ťaháme silou  Fo  kolmou na os, v dôsledku čoho sa dá doska do otáčavého pohybu. Vypočítajte uhlovú rýchlosť a kinetickú energiu dosky po čase  t  od začiatku pôsobenia sily ! Hmotnosť dosky je  m  a polomer R. (Riešte pre hodnoty  m = 20 kg, R = 0,5 m, t = 2 s, Fo =9.81N) Riešenie .

10.  Homogénna tyč všade rovnakého prierezu, hmotnosti  m, dĺžky l voľne visí na vodorovnej osi prechádzajúcej jej koncovým bodom O. Akú minimálnu rýchlosť treba udeliť voľnému koncovému bodu tyče v horizontálnom smere, aby sa dostala do najvyššej možnej polohy ? (Trenie zanedbávame.) (Riešte pre hodnoty   l =  1 m,   m = 2,5 kg  !) Riešenie .

11.  Valec sa valí po naklonenej rovine, ktorá zviera s vodorovnou rovinou uhol α. Polomer valca je  R a hmotnosť  m. a)  Vypočítajte rýchosť jeho ťažiska   po prebehnutí dráhy  s,  keď valec bol voľne pustený. Polomer valca je  R a hmotnosť  m. b)  Porovnajte vypočítanú hodnotu s rýchlosťou, ktorú by malo ťažisko, keby sa valec len šmýkal po dokonale hladkej podložke. a)            b)    .

12.  Vypočítajte kinetickú energiu homogénnej gule rotujúcej okolo priemeru s konštantným uhlovým zrýchlením     v čase  t   od začiatku pohybu ! Hmotnosť gule je  m  a polomer   R.

( Riešte pre hodnoty        t = 10 s,    m = 1,5 kg,   R = 5 cm  )

 

13.  Homogénna kruhová doska polomeru  R   sa nachádza vo vertikálnej  rovine a môže sa otáčať okolo vodorovnej osi kolmej na dosku a vzdialenej od stredu dosky  x.  Dosku vychýlime z rovnovážnej polohy do polohy, v ktorej je  stred dosky vo výške osi a potom ju voľne pustíme. Vypočítajte

a)  začiatočné uhlové zrýchlenie dosky

b)  uhlovú rýchlosť pri prechode rovnovážnou polohou

( Trenie na osi zanedbávajte !)