Odvodenie druhej pohybovej rovnice a zákona zachovania momentu hybnosti

Základné zákony pre pohyb tuhého telesa sa dajú vysvetliť prechodom od sústavy častíc k telesu.

Problém uvedieme riešením pre jednu časticu. Principiálne tým nič nového nedostaneme, pretože ide o „sústavu“ s jednou časticou, a teda s tromi stupňami voľnosti, ktorá je jednoznačne riešiteľná z prvej pohybovej rovnice. Definujeme však nové fyzikálne veličiny, ukážeme ich význam a naznačíme postup všeobecného odvodenia.

Moment hybnosti častice L vzhľadom na daný vzťažný bod O je vektorová veličina daná vektorovým súčinom polohového vektora r častice a hybnosti častice p (Obr. 4.2.2.1).

Moment hybnosti častice závisí od voľby vzťažného bodu. Preto: moment hybnosti je vektor umiestnený do vzťažného bodu O:

(4.2.2.1)

Overme, že pre izolovanú časticu (časticu, na ktorú nepôsobí sila) sa moment hybnosti zachováva, t. j. platí

.

Dosadením a úpravou dostávame:

(4.2.2.2)

Prvý člen je nulový, pretože rýchlosť a hybnosť sú rovnobežné vektory, v druhom člene sme uplatnili zákon zachovania hybnosti:

Pre neizolovanú časticu platí pohybová rovnica

Vynásobením tejto rovnice zľava vektorovo polohovým vektorom a analogickou úpravou ľavej strany ako v rovnici (4.2.2.2) dostávame iné vyjadrenie tejto pohybovej rovnice. (V analógii s rovnicou, ktorú odvodíme pre sústavu častíc alebo teleso, ju môžeme nazvať druhou pohybovou rovnicou pre časticu.) Platí

, (4.2.2.3)

kde moment sily M a moment hybnosti L sú momenty vzhľadom na ten istý vzťažný bod.

Ako príklad uplatnenia rovnice (4.2.2.3) možno uviesť pohyb častice v centrálnom silovom poli (to je napr. pohyb planéty okolo Slnka). Nech je vzťažný bod centrálny bod, potom moment sily je nulový:

,

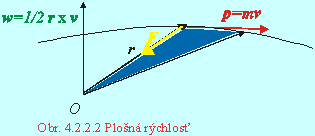
pretože centrálna sila je rovnobežná s polohovým vektorom. Z rovnice (4.3.2.2) vyplýva, že moment hybnosti je konštantný a teda aj plošná rýchlosť (Obr. 4.2.2.2) (definovaná ako veličina číselne sa rovnajúca ploche vytvorenej sprievodičom za jednotku času):

je konštantná:

Uvažujme teraz sústavu dvoch častíc. Využime homogénnosť a izotrópnosť priestoru, t. j. translačnú a rotačnú symetriu priestoru a odvoďme exaktne zákon akcie a reakcie. Všeobecne potenciálna energia vytvorená vzájomným pôsobením dvoch častíc je funkciou polohy týchto častíc:

.

Z homogénnosti priestoru platí:

posunutím sústavy častíc o vektor r_o sa energia nemení a preto je táto len funkciou vzájomného polohového vektora r: W_p(r). Z izotrópnosti priestoru platí, že energia sa nezmení po pootočení sústavy častíc:

.

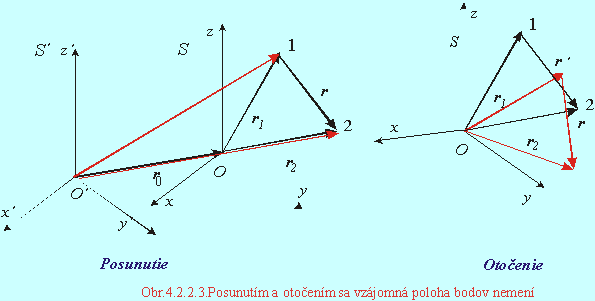
Obr. (4.2.2.3) znázorňuje posunutie voľbou novej súradnicovej sústavy S´, otočenie, otočením sústavy bodov v súradnicovej sústave S. Preto je energia len funkciou vzdialenosti častíc W_p(r).

Ekvipotenciálne hladiny energie častice 2 sú sústredné guľové plochy so stredom v častici 1 a pre silu, ktorou pôsobí častica 1 na časticu 2 platí zo vzťahov odvodených v časti o fyzikálnych poliach

,

sila je rovnobežná s vektorom r. Z tohoto vzťahu rovnako platí pre silu pôsobiacu na prvú časticu, že je daná rovnakým výrazom, zmena je len v tom, že smer určujúci vektor je opačný k vektoru r. Preto tieto dve sily sú vektory opačné ležiace na jednej priamke. To je zákon akcie a reakcie a možno ho zapísať v tvare

.

Podľa vzťahu (4.2.2.3) pre častice platia pohybové rovnice

Ich sčítaním dostávame

Po zovšeobecnení pre izolovanú sústavu N častíc (Na i-tu časticu s momentom hybnosti L_i pôsobí moment sily

je moment sily pôsobiaci na i-tu časticu vytvorený silou, ktorou na ňu pôsobí j-ta častica, celkový moment hybnosti sústavy je súčet momentov jednotlivých častíc:

dostávame zákon zachovania momentu hybnosti pre izolovanú sústavu častíc.

V izolovanej sústave častíc sa celkový moment hybnosti zachováva:

(4.2.2.4)

V neizolovanej sústave častíc na i-tu časticu pôsobí celková sila F_i, ktorá je súčtom všetkých vnútorných na ňu pôsobiacich síl

a vonkajšej sily

.

Pre túto časticu platí pohybová rovnica (4.2.2.3)

Takúto rovnicu môžeme napísať pre každú časticu, sčítajme pravé a ľavé strany rovníc pre všetky častice

,

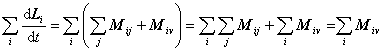kde sme využili, že zo zákona akcie a reakcie súčet momentov vnútorných síl sa rovná nule. Ak zavedieme celkový moment vonkajších síl

a uvážime, že platí

,

dostávame druhú pohybovú rovnicu sústavy častíc:

, (4.2.2.5)

časová zmena celkového momentu hybnosti sústavy sa rovná celkovému momentu vonkajších síl pôsobiacich na túto sústavu.