Odvodenie pohybovej rovnice pre rotačný pohyb okolo pevnej osi

Dosaďme do definície momentu hybnosti pre rotačný pohyb uhlovú rýchlosť otáčania

a využime vzťah pre dvojnásobný vektorový súčin

,

označme

(súradnica priemetu vektora r_o do osi otáčania) a uvedomme si, že uhlová rýchlosť všetkých bodov je rovnaká:

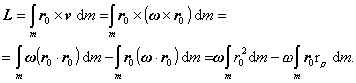(4.2.4.4)

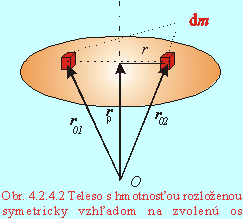
Pre teleso so symetricky rozloženou hmotnosťou vzhľadom na os otáčania pre každý hmotný element dm, zložený z dvoch rovnakých symetricky rozložených častí, platí (Obr.4.2.4.2):

,

kde r_o je priemet vektora r_o do osi otáčania.

Dosadením do predchádzajúceho vzťahu platí:

,

kde sme zaviedli novú veličinu: moment zotrvačnosti vzhľadom na os J:

, (4.2.4.2)

integrál štvorca kolmých vzdialeností hmotných elementov od danej osi cez celú hmotnosť telesa.

Pre teleso, ktoré nemá symetricky rozloženú hmotnosť vzhľadom na danú os vzťah

neplatí, moment hybnosti nemá smer osi otáčania. Jeho priemet do osi otáčania (ktorý potrebujeme do rovnice (4.2.4.1) je daný úpravou rovnice (4,2.4.4) a vzťahmi medzi

,

.

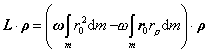Dosadením do rovnice (4.2.4.1) dostávame pohybovú rovnicu pre otáčanie telesa okolo osi

, (4.2.4.3)

na teleso pôsobiaci moment sily vzhľadom na os sa rovná súčinu momentu zotrvačnosti telesa vzhľadom na túto os a uhlového zrýchlenia.