3.2.6 Potenciál gravitačného poľa. Vzťah medzi intenzitou a potenciálom

            Na charakterizovanie vlastností gravitačného poľa sme už zaviedli vektorovú veličinu - intenzitu. Jej  výpočet je však - najmä v prípadoch  systémov diskrétne alebo spojito rozložených hmotných bodov - dosť zložitý. Preto je vhodné zaviesť na tento účel aj nejakú skalárnu veličinu, ktorej výpočet sa realizuje jednoduchšie a ktorá je tiež nezávislá od hmotnosti skúšobného hmotného bodu.

            Takouto veličinou je potenciál gravitačného poľa. Potenciál j v určitom mieste poľa je definovaný ako podiel potenciálnej energie hmotného bodu v danom mieste a hmotnosti tohto hmotného bodu

 

                                                                                                        (3.2.6.1)

 

Ak potenciálnu energiu vzťahujeme na hladinu v nekonečne (absolútna potenciálna energia), potom na rovnakú hladinu vzťahujeme aj potenciál (absolútny potenciál). Tento je v určitom mieste poľa číselne rovný práci, ktorú je potrebné vykonať pri premiestnení hmotného bodu s jednotkovou hmotnosťou z daného miesta do nekonečna. Je zrejmé, že jeho hodnoty (vyjadrené v jednotkách J. kg-1 = m2. s-2) sú záporné.

            Potenciály gravitačného poľa vytvoreného jedným hmotným bodom o hmotnosti M, diskrétnou sústavou hmotných bodov o hmotnostiach M1, M2, ... Mn a spojitou sústavou hmotných bodov (telesom) o celkovej hmotnosti M a objeme V sú postupne

 

                                                                                                     (3.2.6.2)

           

                                                         (3.2.6.3)

           

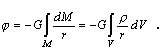                                                                                (3.2.6.4)

           

Plochy v gravitačnom poli, na ktorých je potenciál v každom bode rovnaký, nazývame ekvipotenciálne plochy alebo ekvipotenciálne hladiny. Ak je pole vytvorené len jedným hmotným bodom, ekvipotenciálne plochy majú tvar sústredných  guľových plôch, pričom hmotný bod sa nachádza v ich strede. V rovinnom priereze sa zobrazia systémom sústredných kružníc, ako je to znázornené na obr. 3.2.6.1 prerušovanými čiarami.

            Pri presune hmotného bodu z miesta s potenciálom j1 do miesta s potenciálom j2 sa vykoná práca, rovná rozdielu potenciálnych energií. V zmysle vzťahu (3.2.5.1) môžeme túto prácu zapísať aj ako

 

                                                                                          (3.2.6.5)

 

            Je zrejmé, že pri presune hmotného bodu po ekvipotenciálnej hladine, kde j1 = j2, sa žiadna práca nekoná. Výsledná práca bude nulová pri pohybe v ľubovoľnom smere, keď sa hmotný bod po opustení ekvipotenciálnej hladiny na ňu  vráti; podstatné sú potenciály, resp. ich rozdiel vo východzom a koncovom bode dráhy. Takáto situácia nastane  aj pri obiehaní telesa okolo zdroja poľa po akejkoľvek uzavretej dráhe, aj eliptickej. Príkladmi takýchto pohybov sú pohyby planét okolo Slnka, pohyby družíc okolo Zeme a pod.

 

Odvodíme si teraz súvislosť medzi intenzitou a potenciálom v danom mieste gravitačného poľa.

Ak sa hmotný bod  hmotnosti m  za účinku gravitačnej sily F posunie o dr, gravitačná sila na tomto úseku vykoná prácu dA, ktorá sa rovná úbytku potenciálovej energie  - dEp  hmotného bodu

 

dA = F . dr = - dEp    .                                                                                  (3.2.6.6)

 

Ak túto rovnicu vydelíme hmotnosťou m hmotného bodu, dostaneme

 

                                                                              (3.2.6.7)

           

čiže

 

E . dr = -  dj,                resp.       dj = - E . dr.                                            (3.2.6.8)

 

V gravitačnom poli potenciál j je jednoznačne spojitou funkciou polohy j = j (x, y, z), takže pre úplný diferenciál dj môžeme písať

 

  .                                                                    (3.2.6.9)

 

Takto vyjadrený diferenciál môžeme zapísať aj ako skalárny súčin dvoch vektorov

 

                                          (3.2.6.10)

 

Prvý výraz na prvej strane je vektor, ktorý označujeme ako grad j, druhý výraz vyjadruje  element  posunutia dr, takže

 

dj = grad j . dr   .                                                                                        (3.2.6.11)

 

Po dosadení do (3.2.6.7) dostaneme                                                                          

           

E . dr = - grad j . dr  ,                                                                                  (3.2.6.12)

 

resp.

 

E = - grad j  .                                                                                               (3.2.6.13)

 

Intenzita v danom mieste poľa sa teda rovná zápornému gradientu potenciálu v tomto mieste.

 

Gradient potenciálu, vyjadrený výrazom

 

 

je vektor, ktorého smer udáva smer najväčšej zmeny potenciálu, a jeho veľkosť sa rovná veľkosti tejto zmeny na jednotku dĺžky. Ak sa hmotný bod posunie po ekvipotenciálnej hladine o dr, potenciál sa nemení, takže dj = 0. Potom aj grad j .dr = 0. Pretože oba vektory sú nenulové, môže byť tento predpoklad splnený len vtedy, keď oba vektory sú (podľa vlastností skalárneho súčinu) na seba kolmé. Znamená to, že aj vektory intenzity gravitačného poľa sú kolmé na ekvipotenciálne hladiny.

            Grafické  znázornenie najjednoduchších typov gravitačných polí pomocou  siločiar a ekvipotenciálnych  hladín sú uvedené na nasledujúcich obrázkoch.

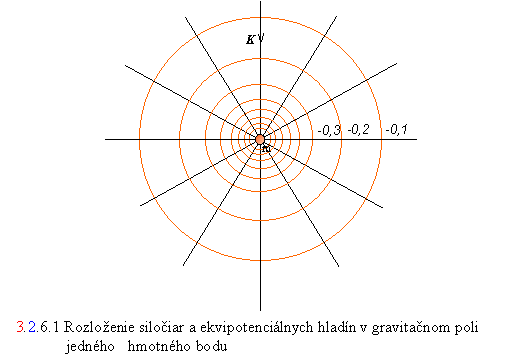
            Na obr. 3.2..6.1 je pole vytvorené jedným hmotným bodom m. Siločiary vstupujú do zdroja poľa, ekvipotenciálne hladiny majú tvar sústredných kružníc okolo neho. Keď ekvipotenciálne hladiny zakreslíme tak, že príslušné hodnoty potenciálu sa  odlišujú vždy o rovnaký rozdiel (napr. Dj = 0,1), potom podľa ich hustoty môžeme posúdiť intenzitu poľa. Ľahko takto zistíme, že  intenzita je najväčšia v tesnej blízkosti zdroja poľa a jej vektor má smer totožný so smerom ubúdania potenciálu.

 

            Na obr. 3.2.6.2 je podobným spôsobom znázornené gravitačné pole, vytvorené dvoma hmotnými bodmi. Siločiary sú zakreslené plnými čiernymi čiarami, ekvipotenciálne hladiny farebnými prerušovanými.

 

 

Kontrolné otázky

 

1.      Definujte veličinu potenciál  gravitačného poľa. V akých jednotkách ho vyjadrujeme?

2.      Ako sa nazývajú plochy, u ktorých je hodnota potenciálu vo všetkých  miestach rovnaká?

3.      Aký je tvar ekvipotenciálnych plôch  v gravitačnom poli, vytvorenom jedným hmotným bodom?

4.      Aký je vzťah (aj inverzný) medzi intenzitou a potenciálom gravitačného poľa? Vysvetlite pojem gradient skalárnej funkcie.

5.      Aká je vzájomná orientácia gravitačných siločiar a ekvipotenciálnych  plôch?

6.      Čomu sa rovná práca, vykonaná pri pohybe hmotného bodu po ekvipotenciálnej ploche? Odpoveď bližšie zdôvodnite.

7.      Ako určíme potenciál v určitom mieste  gravitačného poľa, keď je toto pole vytvorené viacerými hmotnými bodmi?