3.1.3 Druhá
pohybová rovnica
Sústava hmotných bodov vo všeobecnom prípade môže konať
i rotačný pohyb. Pri skúmaní rotačného pohybu, obdobne ako pri hmotnom
bode, vystupujú veličiny moment sily a moment hybnosti sústavy
hmotných bodov, ktoré si zadefinujeme.
3.1.3.1 Moment sily sústavy častíc
Ak na teleso pôsobí vonkajšia sila, z hľadiska jeho
otáčania je dôležité, v ktorom bode na teleso pôsobí. Preto sa zavádza veličina
moment sily (M) vzhľadom na určitý vzťažný bod,
definovaný rovnicou (2.2.3.7),
ako vektorový súčin polohového vektora pôsobiska sily a pôsobiacej sily :
M
= r x f
Poznámka: Vektor momentu
sily sa v slovenskej fyzikálnej literatúre často označuje písmenom D .
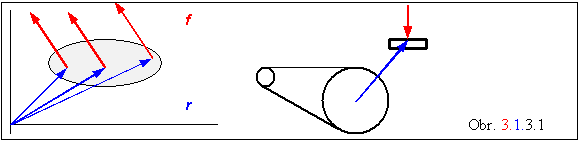
V ľavej časti obrázku 3.1.3.1 je znázornené teleso s tromi alternatívnymi
bodmi pôsobenia rovnakej sily. Ak sila
pôsobí v bode na ľavej strane, začne ho (popri posúvaní) otáčať v smere pohybu
hodinových ručičiek, pri pôsobení na druhej strane opačným smerom. Ak sila pôsobí priamo v ťažisku, začne
teleso iba posúvať. V pravej časti
obrázku je schematicky nakreslený prevod bicykla, pri ktorom krútiaci účinok
sily závisí od vzájomného uhla
polohového vektora r a pôsobiacej sily f
. Moment sily zavedený vzorcom (2.2.3.7) zohľadňuje uvedené skutočnosti, lebo pre
jeho veľkosť platí
M = rf
sin a ,
(3.1.3.1)
čiže vo vzorci vystupuje aj uhol medzi polohovým vektorom a vektorom sily.
Ak je uhol medzi vektormi nulový, alebo = 180 0 , moment sily je
nulový. Zodpovedá to prípadu bicyklového pedálu hornej, alebo dolnej úvrati, kedy zvislé pôsobenie silou na pedál
neprináša úžitok.
Poznámka Vektor momentu sily
pôsobiacej v istom bode telesa závisí od voľby vzťažného bodu. Zmenou vzťažného
bodu sa môže zmeniť ako jeho veľkosť, tak aj smer momentu sily.
V prípade sústavy hmotných bodov, ak na každý pôsobí
sila fk , zavádza sa
výsledný moment síl M vektorovým
súčtom jednotlivých momentov síl Mi
![]() (3.1.3.2)
(3.1.3.2)
Špeciálnym prípadom je dvojica
síl , pod čím rozumieme dve sily
rovnako veľké opačného smeru, neležiace v jednej priamke. Pre sily patriace do
dvojice preto platí f
2 = - f1
a pre moment dvojice síl :
M = M1 + M 2 = (r1 x f1) + (r2 x f2)
= (r1 x f1) - (r2 x f1) = (r1 - r2 ) x f1 ,
takže
M = (r1 - r2 ) x f1
(3.1.3.3)
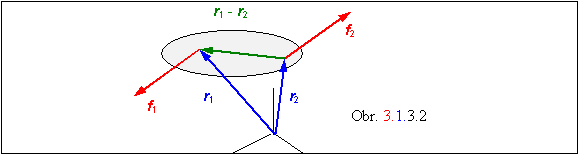
Výsledok ukazuje, že vektor reprezentujúci moment dvojice síl nezávisí
od voľby vzťažnej sústavy, lebo vo výsledku vystupuje rozdiel polohových vektorov (r1 - r2 ) , ktorý je rovnaký v
každej vzťažnej sústave.
3.1.3.2 Moment hybnosti sústavy častíc
Na opis dynamiky otáčavého pohybu sústavy hmotných
bodov a telies sa používa moment
hybnosti (L) ,
ktorý definujme obdobným spôsobom ako
bol definovaný moment hybnosti i -tej
častice (vzťah 2.2.3.6)
vzhľadom na vzťažný bod O, t.j. ako vektorový
súčin polohového vektora hmotného bodu a vektora hybnosti hmotného bodu :
![]() (3.1.3.4)
(3.1.3.4)
kde ri je polohový vektor i -tej častice s hmotnosťou mi vzhľadom na
zvolený vzťažný bod, Hi je hybnosť i -tej častice pohybujúcej sa rýchlosťou vi. Veľkosť a smer vektora momentu hybnosti pohybujúcej sa
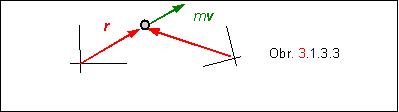
častice závisí od voľby vzťažného bodu, podobne ako moment sily. Na obrázku
obr. 3.1.3.3 sú
znázornené dve vzťažné sústavy. Polohový vektor začínajúci v začiatku sústavy
nakreslenej vľavo, zviera s vektorom hybnosti nulový uhol, preto moment
hybnosti vzhľadom na túto sústavu je nulový.
Deriváciou vzťahu (3.1.3.4) dostaneme
vzťah medzi momentom hybnosti a momentom sily
![]() ,
,
čiže pre i -tu časticu platí rovnica (2.2.3.8)
![]() . (3.1.3.5)
. (3.1.3.5)
Rovnicu (3.1.3.5) možno vysloviť: Moment na i -tu časticu pôsobiacej sily sa
rovná zmene jej momentu hybnosti za jednotku času. Obidva momenty
(sily a hybnosti) vzťahujeme na ľubovolný, avšak pre obidva momenty ten istý vzťažný bod v inerciálnej
sústave. Celkový moment hybnosti
sústavy častíc L je definovaný ako vektorový súčet momentov hybnosti jednotlivých častíc, t.j.
![]() . (3.1.3.6)
. (3.1.3.6)
Pre výsledný moment
síl pôsobiacich na sústavu častíc,
definovaný vzťahom (3.1.3.2),
vzhľadom na zvolený vzťažný bod,
po využití rovnice (3.1.3.6) , dostávame
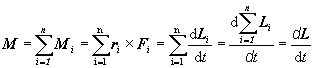
![]() . (3.1.3.7)
. (3.1.3.7)
Porovnaním rovníc (2.2.3.8) a (3.1.3.7) vidíme, že aj v tomto prípade platí medzi
momentom sily hmotného bodu a
vektorovým súčtom momentov síl pôsobiacich na hmotné body sústavy rovnaký
vzťah. Rovnica (3.1.3.7) predstavuje druhú
pohybovú rovnicu pre sústavu hmotných bodov
(častíc).
Integráciou druhej pohybovej rovnice dostaneme druhú impulzovú vetu pre sústavu hmotných bodov :
![]() (3.1.3.8)
(3.1.3.8)
Jej slovná formulácia :
"Impulz momentov všetkých vonkajších síl
pôsobiacich na sústavu hmotných bodov
sa rovná zmene momentu hybnosti sústavy".