3.1.1 Základné kinematické pojmy, hmotný stred sústavy

Zaviedli sme si pojem hmotný bod, pod ktorým rozumieme skúmaný objekt, ktorý má z hľadiska vzájomného pôsobenia s inými objektmi všetky vlastnosti skúmaného telesa, avšak neuvažujeme jeho geometrické rozmery.

Konečný počet hmotných bodov, určitým spôsobom vymedzených voči okoliu, ktoré skúmame ako celok a pritom všetky jednotlivé hmotné objekty patriace do sústavy považujeme za hmotné body, nazveme sústavou hmotných bodov. Ich počet závisí od riešenej problematiky. Za sústavu hmotných bodov možno považovať napr. každé makroskopické teleso, alebo vymedzenú sústavu telies.

Uvažujme n hmotných bodov o hmotnostiach m₁, m₂, ....., m_n. Poloha týchto hmotných bodov v karteziánskej súradnicovej sústave nech je určená polohovými vektormi, r₁, r₂ , ... , r_n. Vzájomnú polohu dvoch hmotných bodov o hmotnostiach m_i a m_j udáva vektor r_ij = r_j –r_i (obr. 3.1.1.1).

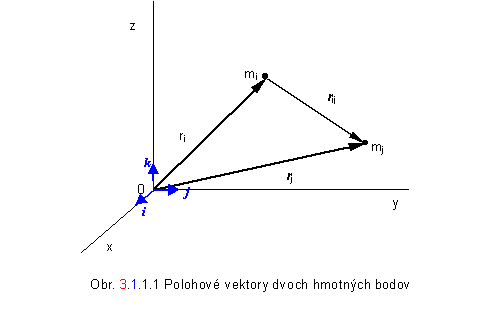
Ak smery i veľkosti r_ij (i=1,2,..., n) sa môžu ľubovoľne meniť, hovoríme o úplne voľných (neviazaných) hmotných bodoch. Ak sú všetky vzájomné vzdialenosti r_ij konštantné, danú sústavu nazývame dokonale tuhou. Existujúce telesá, skladajúce sa z molekúl, resp. z iónov, môžeme považovať za sústavu blížiacu sa k jednému z obidvoch krajných prípadov. Ako aplikáciu prvého stavu, môžeme uviesť ideálny plyn. Druhý príklad možno demonštrovať dokonale tuhou látkou. Častejšie sa stretávame s pojmom dokonale tuhé teleso - teleso, ktorého tvar sa pôsobením vonkajších síl nemení. Tejto problematike sa venujeme vo štvrtej kapitole.

Pri skúmaní pohybu sústavy hmotných bodov je výhodné zaviesť pojem hmotný stred resp. ťažisko. Názov ťažisko, je zaužívaný v spojení s telesom. Ťažisko telesa je bod, ktorým prechádza výslednica všetkých tiažových síl, ktoré pôsobia na hmotné body, z ktorých pozostáva teleso, pri jeho ľubovoľnej polohe v priestore.

V prípade sústavy hmotných bodov, ktoré nevytvárajú kompaktné teleso, je vhodnejšie zaviesť hmotný stred sústavy, t.j. bod, v ktorom má pôsobisko výslednica všetkých tiažových síl, ktoré pôsobia na hmotné body, z ktorých sústava hmotných bodov pozostáva, pri ich ľubovoľnej polohe v priestore.

Poznámka: V homogénnom gravitačnom poli je hmotný stred sústavy hmotných bodov totožný s ťažiskom. Naše ďalšie úvahy sa budú týkať práve takéhoto poľa, preto v ďalšom texte budú pojmy hmotný stred a ťažisko synonymá.

Pre dva hmotné body je hmotný stred bod, ležiaci na ich spojnici, deliaci túto spojnicu v nepriamom pomere hmotností bodov . Na obrázku 3.1.1.2 sú znázornené hmotné body s hmotnosťami m₁ a m₂ , nachádzajúce sa v polohách, ktorým priradíme súradnice x₁ a x₂ . Súradnica hmotného stredu je označená symbolom x_T . Na základe definície platí úmera :

. (3.1.1.1)

Pre súradnicu hmotného stredu platí

x_T = x₁ + p₁ = x₁ + p₂ (m₂/m₁) = x₁ + (x₂ - x_T) (m₂/m₁) .

Z tejto rovnice vyjadríme x_T ako funkciu súradníc x₁ a x₂ :

V trojrozmernom priestore získame analogické vzorce pre ďalšie dve súradnice hmotného stredu

Spojením týchto výsledkov získame vzťah pre polohový vektor ťažiska dvoch hmotných bodov :

(3.1.1.2)

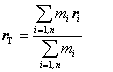
, (3.1.1.3)

respektíve v tvare

,

kde celková hmotnosť sústavy častíc M je daná súčtom hmotností jednotlivých častíc, ktoré sú identifikované indexom i. Index i nadobúda všetky celé čísla od 1 do n .

(3.1.1.4)

Vo zvolenej karteziánskej súradnicovej sústave má polohový vektor r_T hmotného stredu súradnice r_T = [x_T , y_T, z_T], pre ktoré platí

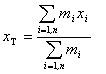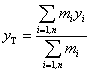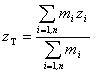, , , (3.1.1.5)

kde x_i, y_i, z_i sú karteziánske súradnice i-teho bodu umiestneného v trojrozmernom priestore.

Hmotný stred je geometrický bod. Jeho poloha vzhľadom na jednotlivé hmotné body danej sústavy nezávisí na voľbe súradnicovej sústavy. Nemusí byť však totožná s polohou niektorého hmotného bodu sústavy.

Pohyb hmotného stredu  často skúmame vzhľadom na sústavu pevne spojenú s hmotným stredom, ktorú nazývame vzťažnou sústavou hmotného stredu. Vzťažná sústava hmotného stredu resp. ťažisková vzťažná sústava, je sústava, ktorej začiatok O je umiestnený do hmotného stredu sústavy hmotných bodov. Vzťažná sústava hmotného stredu je vo všeobecnosti neinerciálna vzťažná sústava. Ak sa však hmotný stred vzhľadom na ľubovolnú inerciálnu sústavu pohybuje konštantnou rýchlosťou (v_T = konšt.), je vzťažná sústava hmotného stredu sústavou inerciálnou.

Počet nezávislých súradníc, ktoré jednoznačne určujú polohu sústavy hmotných bodov vzhľadom na vzťažný bod, je určený počtom stupňov voľnosti sústavy hmotných bodov. Z kinematiky hmotného bodu vieme, že na určenie polohy jedného hmotného bodu sú potrebné tri nezávislé súradnice. Hovoríme, že voľný hmotný bod má tri stupne voľnosti. Ak sústavu hmotných bodov tvorí n hmotných bodov, ktoré sa môžu voči sebe voľne pohybovať, sústava má 3n stupňov voľnosti. Ak pohyb sústavy je určitým spôsobom obmedzený, hovoríme, že sústava je podrobená väzbám, ktoré obmedzujú počet stupňov voľnosti danej sústavy. Ak počet väzieb je v, počet stupňov voľnosti je 3n – v.

_____________________________________

Príklad 3.1.1.1. Pozdĺž osi x sa pohybuje častica s hmotnosťou m₁ tak, že platí x₁ = x_o - v₁ t , a pozdĺž osi y častica s hmotnosťou m₂ tak, že platí y = at²/2 - v₂t . Vypočítajte polohu a rýchlosť ťažiska týchto dvoch častíc ako funkcie času.

Riešenie: a) Súradnice ťažiska vypočítame podľa vzorcov (3.1.1.3) :

Zložením týchto vzorcov dostaneme polohový vektor ťažiska, ako sa mení s časom r_T = x_T i + y_T j .

b) Zapíšeme vektor rýchlosti ťažiska v zložkovom tvare:

v_{T =} v_{T x} i + v_{T y} j ,

pričom platí v_{T x} = (d x_T /dt) , v_{T y} =(d y_T /dt) . Po derivovaní dostávame

v_{T x} = (- m₁v₁ ) / ( m₁ + m₂ ) , v_{T y} = [m₂ .(at - v₂) ] / ( m₁ + m₂ ). Veľkosť rýchlosti ťažiska získame ako odmocninu zo súčtu štvorcov súradníc vektora rýchlosti:

_.

____________________________________________________

Príklad 3.1.1.2. Chlapec drží v rukách dva kamene o hmotnostiach m₁ a m₂ (m₁ > m₂ ), ktoré sú vo vzdialenosti d od seba a vo výške h nad zemským povrchom. Určite: a) súradnice ťažiska sústavy skladajúcej sa z dvoch kameňov, b) časovú závislosť polohy ťažiska pri voľnom páde tejto sústavy súčasne, c) časovú závislosť rýchlosti ťažiska, ak obidva kamene pustíme súčasne, d) súradnice ťažiska sústavy v okamihu t₁ od vypustenia prvého kameňa, ak druhý kameň pustil chlapec z ruky s časovým oneskorením D t, e) veľkosť rýchlosti ťažiska sústavy v okamihu t₁ od vypustenia prvého kameňa, ak druhý kameň pustil chlapec z ruky s časovým oneskorením D t .

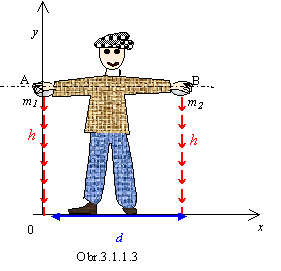
Riešenie: Na obrázku sú zakreslené kamene, ktoré sme umiestnili do bodu A resp. B. Zvoľme si súradnicovú sústavu tak, že bod A leží na y - ovej osi, t.j. A = [0, h ] , B = [d, h ] . Ťažisko sústavy leží medzi bodmi A a B bližšie ku kameňu s väčšou hmotnosťou vo výške y.

Súradnice ťažiska sústavy hmotných bodov sú určené rovnicami (3.1.1.3) a pre dva hmotné body platí

b) Vyjadrime si časovú závislosť súradníc jednotlivých kameňov v prípade, že chlapec púšťa obidva kamene súčasne v okamihu t₀ = 0.

Pre časovú závislosť súradníc ťažiska platí:

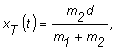
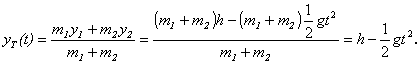
c) Vyjadrime časovú závislosť rýchlosti ťažiska, ak obidva kamene chlapec pustí súčasne:

d) Určime súradnice ťažiska sústavy v okamihu t₁ od vypustenia prvého kameňa, ak druhý kameň pustil chlapec z ruky s časovým oneskorením D t : Nech chlapec pustí ako prvý kameň umiestnený v polohe A. Pre jeho polohu v okamihu t₁ platí

Súradnice druhého kameňa, vypusteného o Dt neskôr po prvom kameni, v okamihu t₁ sú:

Nakoľko x – ové súradnice jednotlivých kameňov nie sú funkciou času, nebude ani x-ová súradnica funkciou času . Súradnice ťažiska v okamihu t₁

e) Vyjadrime veľkosť rýchlosti ťažiska v okamihu t₁: V každom časovom okamihu x-ová zložka rýchlosti ťažiska je nulová, t.j. v_xT (t₁) = 0 a platí

_____________________________

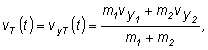
Príklad 3.1.1.3 Z homogénneho kartónu vystrihneme dva útvary A a B, zobrazené na obrázku. Určite:

a) polohu ťažiska jednotlivých útvarov A a B,

b) polohu ťažiska výsledného útvaru, ktorý vznikne spojením, A a B, tak že útvary priložíme k sebe

stranami s veľkosťou b.

Riešenie: Napriek tomu, že sa jedná o výpočet ťažiska telesa, môžeme využiť skutočnosť, že jednotlivé útvary

nahradíme ich ťažiskami a ťažisko útvaru vzniknutého spojením útvarov určíme zo vzťahu (3.1.1.3) pre ťažisko sústavy hmotných bodov.

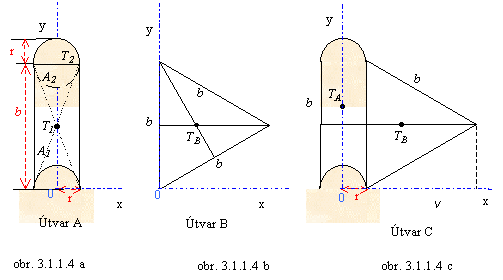
Určíme si najprv polohu ťažiska útvaru A , resp. B. vo zvolenej súradnicovej sústave. Jednou z možností voľby súradnicovej sústavy ukazuje obr. 3.1.1.4 a. y- ova os spadá do osi útvaru A, takže x-ová súradnica ťažiska útvaru A leží na tejto osi, t.j. x_TA = O. Z obrázku vidieť, že útvar A sa skladá z dvoch častí - A₁ obdĺžnika so stranami 2r a b, ktorý ma na obidvoch koncoch vyrezaný polkruh o polomere r, a A₂ kruh s polomerom r. Každý z útvarov A₁ a A₂ možno nahradiť hmotným stredom, v ktorom je sústredená celková hmotnosť m₁ , resp.  m₂. Zo symetrie zvolených útvarov pre polohu ťažiska vo zvolenej súradnicovej sústave platí: x_T1 = x_T2 = 0 , y_T1 = b/2 , y_T2 = b, pričom hmotnosť jednotlivých objektov si vyjadríme pomocou ich plošnej hustoty s a plochy útvarov vzťahmi: m₁ = s S₁ a m₂ = s S₂, kde S₁ = 2r b - pr² , S₂ = pr². Pretože obidve x-ové súradnice sú nulové, bude aj x-ová súradnica ťažiska útvaru A nulová, t.j. x_TA  = 0. Pre y-ovú súradnicu platí

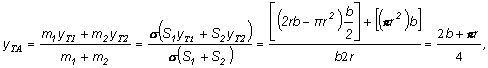
Určíme polohu ťažiska rovnostranného trojuholníka, ktorý si orientujeme tak, ako ho priložíme k útvaru A, ako je znázornené na obr. 3.1.1.4 b, vzhľadom na súradnicovú os y prechádzajúcou stranou b. Ťažisko bude ležať v jednej tretine výšky v od základne , t.j:

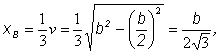
b) Určime ťažisko útvaru vzniknutého spojením útvarov A a B pri orientácii znázornenej na obr. 3.1.1.4 c, vzhľadom na súradnicovú sústavu prechádzajúcu osou útvaru A, v ktorej súradnice

_,

_______________________________________________________________

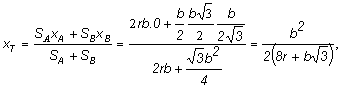
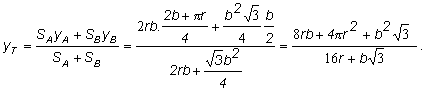
Kontrolné otázky

1. Definujte sústavu hmotných bodov.

2. Určite koľko stupňov voľnosti má hmotný bod pohybujúci sa na guľovej ploche. Uveďte príklad takéhoto pohybu.

3. Definujte hmotný stred sústavy hmotných bodov .

4. Určite polohu hmotného stredu sústavy troch častíc s rovnakými hmotnosťami, umiestnenými vo vrcholoch rovnostranného trojuholníka so stranou a.

5. Vysvetlite súvis symetrie telesa s polohou jeho ťažiska. Uveďte príklady.

6. Závisí poloha ťažiska sústavy hmotných bodov od zvolenej súradnicovej sústavy?

7. Zvážte koľko existuje možností vytvorenia výsledného objektu zložením  dvoch objektov A a B z príkladu (3.1.1.4 ). Zmení sa poloha ťažiska?

8. Zapíšte vzťah pre polohu hmotného stredu sústavy hmotných bodov nachádzajúcich sa v rovine xz.