2.2.6 Zákon
zachovania energie
Ak
na mechanickú sústavu nepôsobia vonkajšie sily a teda podľa zákona o akcii a
reakcii ani sústava nepôsobí silami na okolité telesá, sústave sa nedodáva, ani
z nej neodoberá práca. Preto sa energia
sústavy nemení. Túto skutočnosť vyjadrujeme formuláciou - energia izolovanej sústavy sa nemení. Je
to formulácia zákona zachovania energie mechanickej sústavy.
Tento zákon možno formulovať
aj matematicky. Na tento účel použijeme príklad z pohybu častice v gravitačnom
poli Zeme.
Gravitačná sila pôsobiaca na
časticu koná prácu na úkor potenciálnej energie častice, pričom aj zo
skúsenosti vieme, že zväčšuje jej rýchlosť, teda kinetickú energiu častice.
Sústavu Zem - častica považujeme za izolovanú,
preto jej celková energia sa zachováva. Vzájomnou príťažlivosťou Zeme a častice
sa obe telesá začnú k sebe približovať, pravda pohyb Zeme v porovnaní s pohybom
častice je zanedbateľný (pozri príklad 2.2.6.3). Preto zákon
zachovania energie v tomto prípade formulujeme tak, ako by sa týkal iba
častice : úbytok potenciálnej energie častice v
gravitačnom poli Zeme sa rovná prírastku kinetickej energie častice.
Preto vzťah (2.2.5.9) môžeme
zapísať v tvare :
fy dy = - dEp
= +dEk ,
odkiaľ vyplýva
dEk
+ dEp =
0 Þ d (Ek + Ep) =
0 Þ

Súčet kinetickej a potenciálnej energie
častice sa s časom nemení. To znamená, že ak v časovom okamihu t1 má častica energie Ek1 a Ep1
, a v časovom okamihu t2 energie Ek2 a Ep2 , potom platí rovnosť
Ek1 + Ep1 = Ek2 +
Ep2 (2.2.6.2)
_____________________________
Príklad 2.2.6.1
Pomocou zákona zachovania mechanickej energie vypočítajte, akou
rýchlosťou dopadne teleso padajúce voľným pádom z výšky h . Hmotnosť telesa je m
.

Riešenie:
Nech h = y1 - y2 . Vo výške označenej súradnicou y1
nech má teleso nulovú kinetickú
energiu, Ek1 = 0, a potenciálnu energiu Ep1
= mgy1 . Voľným pádom
teleso padá nadol a v polohe označenej súradnicou y2 má menšiu
potenciálnu energiu Ep2 = mgy2 a
neznámu kinetickú energiu mv22 /2 . Podľa
vzorca (2.2.6.2 platí rovnosť
0 + mgy1
= mv22/2 + mgy2 ,
odkiaľ najprv
osamostatníme kinetickú energiu :
mv22/2 = mg(y1 - y2) = mgh ,
a vypočítame rýchlosť
v2 = (2gh)1/2
_______________________________
Poznámka: Rovnaký výsledok dostaneme pre rýchlosť vody
prichádzajúcej do turbíny po prekonaní výškového rozdielu h . Ak poznáme
prierez potrubia, pomocou vypočítanej rýchlosti môžeme zistiť, koľko
mechanickej energie za sekundu voda prináša do turbíny.
________________________________
Príklad 2.2.6.2
Akú rýchlosť v treba udeliť
guli smerom nahor po naklonenej rovine s uhlom
a = 300 , aby prebehla
dráhu s = 5 m ? (Nebudeme uvažovať trenie, ani odpor prostredia.)
Riešenie: Dohodneme sa, že
na začiatku má guľa nulovú potenciálnu energiu, Ep1 =0 . Jej začiatočná kinetická energia Ek1 = mv2/2. Pri pohybe nahor po naklonenej
rovine postupne nadobúda výšku a stráca rýchlosť. Na konci dráhy s bude mať nulovú kinetickú energiu Ek2
= 0 , pričom jej potenciálna energia bude
Ep2 = mgh = mgs
sin(30o). Použijeme vzorec (2.2.6.2) , pomocou ktorého získame vzťah
mv2/2
+ 0 = 0 + mgs sin(30o) ,
z ktorého
vypočítame začiatočnú rýchlosť :
v = (gs)1/2 @ (10 ms-2
. 5 m )1/2 = (50 m2 s-2 )1/2 @
7 ms-1
___________________________________
Príklad 2.2.6.3 Teleso s
hmotnosťou m začne vplyvom gravitačnej
sily padať na Zem. Teleso a Zem sa navzájom priťahujú, preto po uplynutí istého
časového intervalu obe telesá nadobudnú istú rýchlosť, ktorú meriame vzhľadom
na vzťažnú sústavu spojenú s ich ťažiskom. Posúďte, či kinetické energie týchto
telies sú po uplynutí časového intervalu
Dt rovnaké.
Riešenie: Podľa zákona
akcie a reakcie sily, ktorými telesá na
seba pôsobia, sú rovnako veľké, preto
telesám udelia rovnako veľký impulz I = F Dt .
Predpokladáme, že na začiatku boli telesá v pokoji, takže po uplynutí
časového intervalu Dt
nadobudnú rovnaké hybnosti :
Mw = mv , kde M je hmotnosť Zeme a m hmotnosť telesa.
Rýchlosť Zeme w v porovnaní s rýchlosťou telesa v
je malá, lebo zo zákona
zachovania hybnosti vyplýva
![]() .
.
Kinetická energia
Zeme je
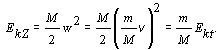
Pomer kinetických energií Zeme a telesa je nepriamo
úmerný pomeru ich hmotností :
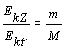
Preto je
kinetická energia Zeme zanedbateľná. (Hmotnosť Zeme M = 5,98
. 1024 kg)
Kontrolné otázky
1. Definujte
celkovú mechanickú energiu hmotného bodu.
2. Aký poznatok
platí pre izolovanú sústavu? Uveďte príklady izolovanej sústavy.
3. Vyslovte zákon
zachovania mechanickej energie.