2.2.4    Práca a výkon

 

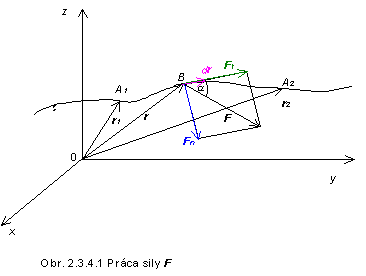
      Pod prácou rozumieme pôsobenie sily po dráhe.  V zjednodušenom vyjadrení pod prácou rozumieme súčin sily a posunutia častice (telesa), na ktoré sila pôsobí.  Nech pôsobením sily F na hmotný bod sa tento hmotný bod posunie po určitej dráhe z bodu A1 o polohovom vektore r1 do bodu A2 o polohovom vektore r2 . V  tomto prípade hovoríme o dráhovom účinku sily, resp. o práci sily F po  uvažovanej krivke (obr. 2.2.4.1), ktorú definujeme pomocou  integrálu

 

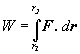  .                                                                                               (2.2.4.1)

    

V definícii vystupuje skalárny súčin sily a elementárneho posunutia, čo znamena, že v skalárnom tvare vystupuje kosínus uhla, ktorý zvierajú vektory   F   a  dr  .   Z uvedeného vzťahu vidíme, že práca sily F závisí nielen od pôsobiacej sily,  od počiatočného   a  koncového bodu trajektórie, po ktorej sa pôsobisko sily pohybuje, ale aj na vzájomnej orientácii vektora sily F a vektora posunutia dr. To znamená, že ak vektory sily a posunutia sú na seba kolmé, sila prácu nekoná. Sila sa efektívne využíva na konanie práce vtedy, ak má smer posunutia.

 Práca je skalárna fyzikálna veličina.     Jednotkou práce v sústave SI je 1 J ( joule).

1 J = 1 N.m = 1 kg.m2.s-2. Joule (1 J) je práca , ktorú vykoná konštantná sila 1 N pôsobiaca po dráhe 1 m v smere sily. V molekulovej a atómovej fyzike sa používa často jednotka 1 eV (elektronvolt), 1 eV = 1,602. 10-19 J. V elektrotechnike sa stretávame s ďalšou jednotkou práce 1 kWh  (kilowatthodina), ktorá vyplýva z definície výkonu , o ktorom  ešte pojednáme 1 kWh = 3,6. 106 J

 

 

            Vo všeobecnosti sila  počas pohybu môže meniť svoju veľkosť i smer. Pri elementárnom posunutí dr možno silu F považovať za konštantnú. Prácu pri elementárnom posunutí nazývame  elementárnou  prácou  a jej veľkosť možno určiť vzťahom

 

.                                                             (2.2.4.2)                                             

 

Rozložme pôsobiacu silu v ľubovolnom bode trajektórie na zložku Ft  - rovnobežnú s elementárnym posunutím dr   a na zložku Fn  kolmú na smer posunutia. Dráha bodu môže byť určená väzbou,  napríklad podložkou.  Sila Fn  sa ruší silou,  ktorou pôsobí podložka na hmotný bod. Za predpokladu, že máme určenú silu  i trajektóriu možno vyjadriť prácu vzťahom

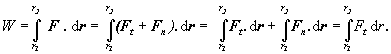                    (2.2.4.3)                                                              

 

Rovnica (2.2.4.3)  vyjadruje skutočnosť, že ak smer sily a dráhy nie je rovnaký, prácu koná len zložka sily v smere dráhy,  čo možno zapísať

 

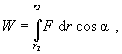                                                                                       (2.2.4.4)     

 

kde a  je uhol, ktorý zviera smer  vektora sily s vektorom posunutia. Ak vektor sily je konštantný, t.j. F = konst., z rovnice (2.2.4.4) vyplýva, že práca nezávisí na tvare dráhy. Prácu konštantnej sily po úsečke dĺžky l (l-dĺžka trajektórie medzi počiatočným bodom A a koncovým bodom B) je daná súčinom priemetu sily do smeru úsečky a dĺžky úsečky, nakoľko

 

 

.

 

 

­­­­­­­­­­­­­­­­­­­­­­­­­­­­­____________________________

 

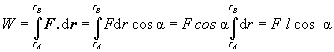
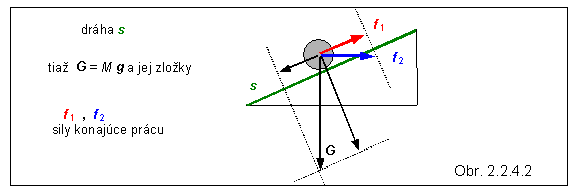
Príklad  2.2.4.1 Po naklonenej rovine, ktorej dĺžka je  s = 2 m a sklon  30o , posúvame bremeno s hmotnosťou  M = 30 kg . Ak neuvažujeme trenie, akú veľkú prácu treba vykonať na posunutie bremena? Pritom môžeme pôsobiť silou, ktorá je rovnobežná s naklonenou rovinou, alebo silou, ktorá má horizontálny smer. Posúďte, či v týchto prípadoch vykonáme odlišnú prácu, a či pritom treba pôsobiť odlišnými silami !                

 

 

Riešenie : Sila, ktorou pôsobíme na bremeno, musí kompenzovať zložku tiaže bremena, rovnobežnú  naklonenou rovinou. Táto zložka tiaže smeruje pozdĺž naklonenej roviny nadol, preto zložka sily ktorou chceme bremeno posúvať po rovine nahor,  musí byť rovnako veľká a smerovať nahor (na obrázku sila f 1 ). Ak by sme pôsobili silou vodorovne (sila  f 2 ), táto by musela byť väčšia , aby jej zložka rovnobežná s naklonenou rovinou mala rovnakú veľkosť, ako sila f1  .  Práca síl  f 1  a   f 2  pri posunutí bremena po dráhe  s  je rovnaká, lebo v prípade sily f 2  sa pri práci uplatňuje iba jej zložka rovnobežná s naklonenou rovinou. Veľkosť vykonanej práce :  W = Mg . sin(300) . s  =  30 kg . 9,81 m/s2 . 0,5 . 2 m  @ 300 J .   

___________________________

 Príklad  2.2.4.2  Vypočítajte akú veľkú prácu vykonal elektromotor výťahu, ktorý zdvihol obsadenú kabínu (500 kg) z prízemia na piate poschodie (t.j. 15 m) .       

Riešenie : Na dvíhanie kabíny s hmotnosťou  m = 500 kg je potrebná sila  F = mg , kde  g = 9,81 ms-2 je tiažové zrýchlenie. Takáto sila musí pôsobiť po dráhe  s = 15 m. Práca vykonaná elektromotorom je

 W = mgs = 500 kg . 9,81 ms-2 . 15 m  = 73 575 kg.m2.s-2 = 73575 J .

________________________________________

Príklad 2.2.4.3  Vyjadrite prácu tiažovej sily pri posunutí jej pôsobiska z bodu A o súradniciach [0, yA, 0]  do bodu B  [0, yB., , 0] 

Riešenie: V karteziánskej súradnicovej sústave vyjaríme si  vektor tiažovej sily  FG =  - mg j a vektor posunutia

 dr  =dx i + dy j +dz k, ktoré dosadíme do vzťahu (2.2.4.2)                                             

 

 

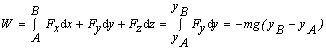
Z posledného výrazu vyplýva, že práca tiažovej sily závisí len od počiatočnej a konečnej y-ovej súradnice trajektórie  a nezávisí na tvare trajektórie.  V prípade, že hmotný bod:

znižuje svoju výšku                                yA   > yB        W  > 0    t.j. práca tiažovej sily je kladná;

zvyšuje svoju výšku                               yA   < yB        W  < 0    t.j. práca tiažovej sily je záporná;

nezmení svoju výšku pri premiestnení    yA  = yB        W  = 0    t.j. tiažová sila nekoná  prácu.

–––––––––––––––––––––––––––

Ak práca sily nezávisí na trajektórii, ale len na počiatočnom a koncovom bode trajektórie, nazývame túto silu konzervatívnou. Práca konzervatívnych síl po uzavretej krivke je nulová. Príkladom konzervatívnych síl sú sila tiažová a sila gravitačná,  ktorým sa budeme venovať v osobitných paragrafoch tretej kapitoly. V prípade, že práca sily závisí na trajektórii, hovoríme o silách nekonzervatívnych resp. disipatívnych. Príkladom disipatívnych síl je sila trenia a sila odporu prostredia.

 

Výkon definujeme ako prácu vykonanú za jednotku času. Výkon  je preto podiel vykonanej práce DW a príslušného časového intervalu  Dt :     P  =  DW /  Dt . (Hovoríme o strednom alebo priemernom výkone.) V rovnakých časových intervaloch nasledujúcich za sebou, môže byť vykonaná práca rôzna,  výkon sa môže od okamihu k okamihu meniť. Preto presná definícia okamžitého  výkonu sa zavádza ako limita vyššie uvedeného podielu :

 

                                                              (2.2.4.5)     

 

Modifikáciou tohto vzorca možno získať vzťah medzi pôsobiacou silou (napríklad ťažnou silou motora dopravného prostriedku) a rýchlosťou pohybu pôsobiska sily :

 

                                        (2.2.4.6)     

 

Z výsledku vyplýva, že pri danom výkone motora  dopravného prostriedku s rastúcou rýchlosťou klesá jeho ťažná sila.  

 

Jednotkou výkonu v SI je  watt  (W) , pričom  1 W = 1 J/s  (joule za sekundu). V praxi sa často používajú dekadické násobky a diely tejto jednotky -  kilowatt (kW), megawatt (MW), a gigawatt (GW), najmä v energetike. V elektronike sa používajú diely - miliwatt (mW), a mikrowatt (mW).

 

            Pri vyjadrovaní práce v SI sústave  rovnocennou jednotkou  joulu  je  wattsekunda,

 1 J = 1 Ws .   V energetike je však frekventovanejšie používanie väčších jednotiek :

 1 Wh (watthodina) = 3600 Ws = 3,6 . 103  Ws

 1 kWh (kilowatthodina) =  1000 Wh = 3,6 . 106 Ws

 1 MWh (megawatthodina) = 3,6 . 109 Ws

 

            Pri dodávaní elektrickej, alebo aj inej energie do pracujúceho stroja sa hovorí o príkone  , čím sa rozumie energia dodávaná za jednu sekundu. Aj príkon sa meria vo wattoch. Nie všetku dodanú energiu stroj zúžitkuje - práca za sekundu, ktorú vykoná - jeho výkon, je menší ako príkon. Podiel odvádzaného výkonu a stroju dodávaného príkonu je účinnosť stroja. Udáva sa buď priamo ako zlomok, alebo v percentách. Účinnosť stroja nikdy nemôže dosiahnuť  100 %, musel by pracovať bez akýchkoľvek strát.

____________________________________

Príklad  2.2.4.4   Remenica má polomer  R = 10 cm. Aký veľký je rozdiel medzi silami, ktorými je napínaný remeň na  dvoch stranách  remenice,  keď  sa ním  pri  frekvencii  otáčania  remenice f = 10 s-1  prenáša  príkon P = 2 kW ?

 

 

 

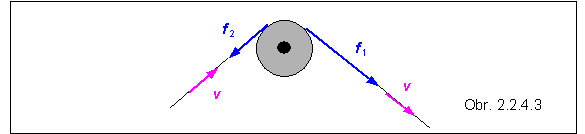
Riešenie :   Remeň sa pohybuje rýchlosťou  v = R . 2p f = 2p m/s. Výkon na strane väčšej sily je  P1 =   F1  v . Na druhej strane remenice výkon P2 =   F 2 v   je záporný, lebo vektory v  a   f 2  smerujú proti sebe. Prenášaný výkon sa rovná súčtu výkonov :

 

 P = P1 + P2  =  (F1 - F2 ) v   ,

 

odkiaľ získame rozdiel síl, ktorými je napínaný remeň pred a za remenicou :

 

 (F1 - F2 )  =  P / v    =  2.103 / 2p  =  1000/p  N .

_____________________________________

Príklad  2.2.4.5  Aký musí byť príkon elektromotora z príkladu 2.2.4.2 , keď má dopraviť kabínu výťahu na piate poschodie za 15 sekúnd ? Účinnosť elektromotora je 80%. 

Riešenie :   Elektromotor musel vykonať prácu W = 73575 J za  Dt = 15 s, musel teda pracovať s výkonom

 

  Pv  =  W / Dt  =  4 905 J/s = 4 905 W @ 4,9 kW .

 

 Tento výkon predstavuje 80% príkonu, t.j.  

 

Pv  =  0,8  Pp    , takže   Pp  =  Pv / 0,8   @ 6,13 kW

_____________________________________

 

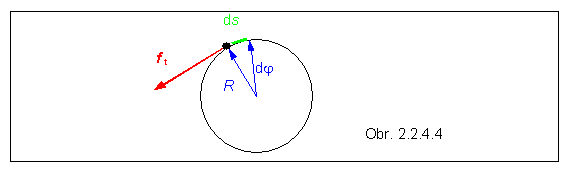
                Pri pohybe častice viazanej pevne na kružnicu, pre konanie práce má význam iba tangenciálna zložka sily  f t , lebo tá je rovnobežná s elementárnym posunutím častice v každom bode kružnice.  Pre elementárnu prácu takejto sily platí :

 

dW  =  f tdr  =  f t  ds  =  f t R dj  =  M dj  ,                                                (2.2.4.7)     

 

takže pre prácu tangenciálnej sily, ktorá urýchľuje (alebo brzdí) časticu v pohybe po kružnici platí

                                        (2.2.4.8)     

   

 

Pre výkon tangenciálnej sily v takomto prípade môžeme upraviť vzorec (2.2.4.6) :

 

P  =  f v  =  f t v  =  f t Rw  =  Mw,                                                               (2.2.4.9)

 

kde   M  =  f t R   je veľkosť momentu tangenciálnej sily.

______________________________

Príklad  2.2.4.6  Akú veľkú prácu vykonala tangenciálna sila  F t  pôsobiaca na obvode valca s polomerom  R, keď sa valec otočil  n - krát .  

Riešenie :  Použijeme vzorec (2.2.4.8) :  W = M Dj =  (F t  R) (n 2p) = F t n 2pR .   

K rovnakému výsledku dospejeme, ak uvážime, že tangenciálne sila F t  sa musela posunúť po priamej dráhe o vzdialenosť  s  =  n 2pR  , takže vykonala prácu  W =   F t  s  =  F t n 2pR   .

_______________________________

Príklad  2.2.4.7  Aký výkon sa prenáša tangenciálnou silou veľkosti  F t  =  1000 N  na hriadeľ motora  s polomerom R = 0,25 m , pri   frekvencii hriadeľa  3000 /min  ?

Riešenie :   Použijeme vzorec  (2.2.4.9) :   P  =  M w =  (F t  R) 2p f  =  (1000 N . 0,25 m) . 2p . 50 s-1  =  78 540 N.m/s   =  78,54 kW .

_______________________________

 

Kontrolné otázky

 

1.      Definujte pojem elementárna  práca a matematicky ju sformulujte.

2.      Napíšte jednotku práce v sústave SI.

3.      Aké účinky sily poznáme?

4.      Vysvetlite kedy je vykonaná práca maximálna a kedy minimálna?

5.      Ak smer sily a dráhy nie je rovnaký, ktorá zložka sily koná prácu?

6.      Otec i malý syn ťahajú rovnakou silou, po rovnakej dráhe každý svoje rovnaké sánky. Vykonajú obaja  rovnakú prácu? Svoju odpoveď matematicky zdôvodnite.

7.      Definujte  stredný a okamžitý výkon a určite jeho jednotku pomocou  základných jednotiek sústavy SI.

8.      Kedy bude mať teleso pri dopade na zem väčšiu rýchlosť: ak padá z výšky h voľným pádom, alebo keď sa pohybuje bez trenia po naklonenej rovine z rovnakej výšky?

9.      Tlstý chlapec a chudý chlapec sa šmýkajú bez trenia po rovnakej šmýkačke.  Ktorý z nich dosiahne väčšiu rýchlosť pri dopade? (Trenie zanedbáme.)

10.  Rozhodnite, či pri pohybe skúmaného hmotného bodu (telesa)  po naklonenej rovine do výšky h treba taká istá sila ako pri zdvíhaní toho istého telesa do tej istej výšky. Svoje tvrdenie matematicky zdôvodnite.

11.  Ak vektor sily je konštantný, t.j. F = konst.,  ukážte, že práca nezávisí na tvare dráhy.

12.  Vyjadrite  jednotku práce v základných jednotkách SI sústavy.

13.  Vyjadrite  jednotku práce „Ws“ v základných jednotkách SI sústavy.

14.  Definujte účinnosť stroja.