2.2.2 Pohyb v neinerciálnej sústave

Vzorec (2.1.11.4) v paragrafe 2.1.11 vyjadruje súvislosť medzi zrýchleniami častice pozorovanými v dvoch vzťažných sústavách- inerciálnej a neinerciálnej :

a = a_o + a ' + ( a ´ r ' ) + 2(w ´ v' ) + [w ´ (w ´ r ' )] .

Ak by obe sústavy boli inerciálne, museli by sa navzájom pohybovať konštantnou rýchlosťou, čiže a_o = 0, a = 0, w = 0 . Potom a = a ' , takže zrýchlenie častice v oboch sústavách je rovnaké. (Vo všetkých inerciálnych sústavách nameriame častici rovnaké zrýchlenie). Ak však medzi zrýchleniami pozorujeme rozdiel w = a - a ' , jedna zo sústav je neinerciálna. Vynásobením posledného vzťahu hmotnosťou častice m dostaneme vzťah :

ma ' = ma - m w.

Súčin ma , teda súčin hmotnosti častice a zrýchlenia v inerciálnej sústave, podľa druhého Newtonovho zákona sa rovná sile pôsobiacej na časticu. Táto sila môže mať pôvod iba v jednej zo štyroch fyzikálnych interakcií - gravitačnej, elektromagnetickej, jadrovej silnej, alebo jadrovej slabej. Hovoríme jej skutočná sila. Preto označíme ma = F_fyz . V neinerciálnej sústave potom platí

ma ' = F_fyz + F_zotrv , (2.2.2.1)

pričom výraz - m w sme označili ako F_zotrv , nazývame ho zotrvačná sila a môže pozostávať z viacerých členov :

- m w = - m a_o - m (a ´ r ' ) - m 2(w ´ v' ) - m [w ´ (w ´ r ' )] , (2.2.2.2)

ktoré možno vyjadriť vektorovým súčtom

F´ = F_fyz + F₀ + F_c + F_od + F_{E .} (2.2.2.3)

Význam jednotlivých členov v rovnici (2.2.2.2) je:

· F_fyz je vonkajšia sila pôsobiaca na hmotný bod, majúca pôvod vo vzájomnom pôsobení materiálnych objektov na hmotný bod.

· F₀ = - m a₀ je tzv. postupná zotrvačná sila, vznikajúca v dôsledku zrýchleného pohybu začiatku sústavy S. Pozorovateľovi vo vnútri neinerciálnej sústavy sa javí, že táto sila sa snaží zrýchľovať tento hmotný bod vzhľadom k tejto sústave.

· F_C = - 2 m(w ´ v´) je tzv. Coriolisova sila, ktorá pôsobí na telesá pohybujúce sa v neinerciálnej sústave rýchlosťou v ´ rôznobežnou s osou otáčania. Jej veľkosť závisí od orientácie vektorov w a v ´ .

· F_od = - m w ´ (w ´ r´) je tzv. zotrvačná odstredivá sila. Táto sila má pôvod v rotačnom pohybe sústavy. Často sa stretávame s jej názvom ako radiálna príťažlivá sila.

· F_E = - (a x r¢ ) je tzv. Eulerova sila, ktorá je od nuly rôzny vtedy, keď uhlová rýchlosť otáčania nie je konštantná, ale sa mení s časom.

Všetky štyri zotrvačné sily F₀ , F_c , F_od a F_E sa javia pozorovateľovi v pohybujúcej sa neinerciálnej sústave ako sily poľa, pretože nie sú spôsobené dotykom iných telies. Ich zmysel si ozrejmíme na situáciách, s ktorými sa stretávame v bežnom živote:

Uvedieme tri konkrétne príklady.

1. Pri rozbiehaní dopravného prostriedku zrýchlením a_o cestujúci pociťuje, že do chrbta ho tlačí operadlo, pričom operadlo je počas rozbiehania mierne ohnuté. Za mieru sily pôsobiacej na cestujúceho môžeme považovať deformáciu operadla. Pozorovateľ tejto udalosti nachádzajúci sa v inerciálnej sústave (viazanej na autobusovú zastávku) vidí, že cestujúci sa pohybuje zrýchleným pohybom, čo si vysvetlí silou pôsobiacou na cestujúceho, pochádzajúcou z ohnutia operadla (keď si pravdaže odmyslíme autobus). Pozorovateľ viazaný na autobus, teda neinerciálnu sústavu, vidí, že cestujúci aj sedadlo sú v pokoji, jeho zrýchlenie je nulové, ale vidí, že operadlo je deformované. Preto usúdi, že na cestujúceho pôsobí sila, ktorá sa prenáša na operadlo, ale nepozná jej príčinu. Zodpovedá členu - m a_o rovnice (2.2.2.2). Rovnako veľké, spätné pôsobenie operadla na cestujúceho, udržiava ho v neinerciálnej sústave v pokoji. V inerciálnej sústave skutočná sila, ktorej pôvod je v deformácii operadla, vyvolá zrýchlenie cestujúceho, v neinerciálnej je kompenzovaná zotrvačnou silou. Pritom zotrvačná sila nemá pôvod v niektorej z vyššie uvedených fyzikálnych interakcií.

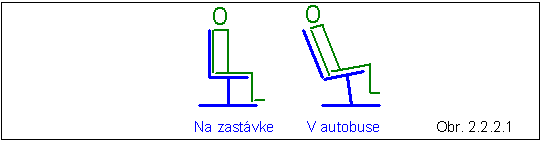
Keby na zastávke bolo podobné sedadlo s cestujúcim, nebol by dôvod na ohnutie operadla, lebo je vzhľadom na inerciálnu sústavu v pokoji. Ale pozorovateľ z rozbiehajúceho sa vozidla vidí, že vzhľadom na jeho sústavu sa čakajúci cestujúci spolu so sedadlom pohybuje zrýchleným pohybom. Ani on nepozoruje, že by operadlo sedadla bolo deformované. Pozorovateľ z neinerciálnej sústavy musí zrýchlený pohyb čakajúceho cestujúceho a jeho stoličky vysvetliť pôsobením zotrvačných síl, pričom nepozoruje reakciu na tieto sily.

Zotrvačné sily, ktorým hovoríme aj fiktívne sily, nemajú reakciu.

2. Na rotujúcom disku je o jeho os pružinou pripevnený kváder, ktorý rotuje spolu s diskom, pričom sa môže po jeho povrchu hladko kĺzať. Čím väčšia je uhlová rýchlosť w otáčania disku, tým je kváder od osi ďalej. Pozorovateľ stojaci vedľa disku (v inerciálnej sústave) pozoruje predĺženie pružiny, čo je v súlade so skutočnosťou, že ak sa má kváder pohybovať po kružnici, musí naň pôsobiť dostredivá sila, realizovaná natiahnutím pružiny. Pre "neinerciálneho" pozorovateľa viazaného na otáčajúci disk je kváder v pokoji, a deformáciu pružiny pripíše pôsobeniu zotrvačnej sily na kváder, ktorú v tomto prípade nazývame odstredivá sila.

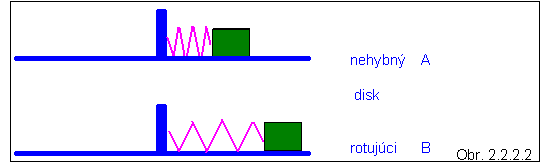
Táto sila zodpovedá členu - m [w ´ (w ´ r ' )] rovnice (2.2.2.2). Podobne ako v prvom príklade, aj teraz môžeme uvažovať s dvomi diskami - rotujúci disk B, predstavuje neinerciálnu sústavu, nehybný A, inerciálnu sústavu. Pozorovateľ viazaný na disk B konštatuje, že jeho disk je v pokoji (podobne ako my, viazaní na našu Zem), a že sa otáča disk A (opačným smerom ako rotujúci disk). Napriek tomu však vidí, že predĺžená je pružina na jeho disku. Preto musí toto predĺženie vysvetliť fiktívnou odstredivou silou. Keď sa pozrie na disk A (nad ním), vidí že sa otáča, ale pružina nie je predĺžená. Z tohto skúsený a vzdelaný pozorovateľ môže urobiť iba jeden záver - že v skutočnosti sa otáča jeho sústava B.

Zotrvačnú odstredivú silu pozorujeme aj vo vzťažnej sústave viazanej na našu Zem.

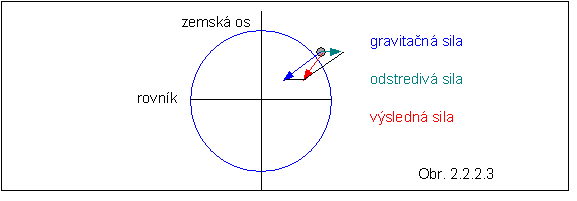
Na obrázku je zachytená situácia na rovnobežke zodpovedajúcej približne polohe našej krajiny. Veľkosť odstredivej sily tu predstavuje len 0.23 % veľkosti gravitačnej sily, čo však pri precíznych gravimetrických meraniach predstavuje nezanedbateľnú zložku nameranej hodnoty. Ako vidno z obrázku, výsledná sila je menšia ako gravitačná.

3. Na disku rotujúcom uhlovou rýchlosťou w je vyčnievajúce rebierko siahajúce od

stredu disku až po jeho okraj. Pozdĺž rebierka sa od stredu disku kotúľa guľka konštantnou rýchlosťou v' vzhľadom na disk.

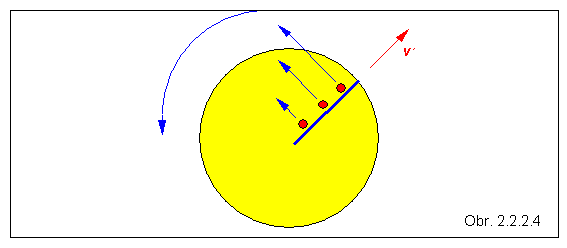
Vzhľadom na disk ide o pohyb priamočiary rovnomerný. Pre pozorovateľa mimo disku sa guľka pohybuje po špirále. Keď je guľka ďalej od stredu disku, nachádza sa na kružnici s väčším polomerom, takže má aj väčšiu obvodovú rýchlosť. Preto má v inerciálnej sústave tangenciálne zrýchlenie, ktoré je vyvolané silou 2m(w ´ v' ) sprostredkovanou rebierkom na disku. Sila má smer dotyčnice tej kružnice, na ktorej sa guľka práve nachádza. Guľka spätne pôsobí na rebierko silou reakcie. Pre pozorovateľa spojeného s diskom guľka nemá v jeho sústave zrýchlenie. Tento pozorovateľ však zaregistruje, že guľka na rebierko pôsobí silou -2m(w ´ v' ), čo je v jeho sústave zotrvačná Coriolisova sila. Aj túto silu možno pozorovať na našej Zemi. Na obrázku je znázornená Zem s rovníkom a vybraným poludníkom. Namiesto guľky si predstavme tečúcu rieku od severu na juh pozdĺž poludníka rýchlosťou v ' .

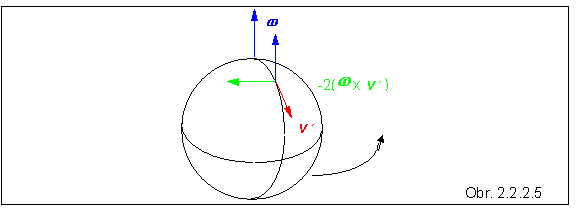
Voda v rieke tečie smerom k rovníku, teda od rovnobežiek s menším polomerom k rovnobežkám s väčším polomerom. Musí byť urýchľovaná v tangenciálnom smere - kolmo na smer svojej rýchlosti. Preto na ňu pôsobí pravý breh rieky, ktorý sa vymieľa rýchlejšie ako ľavý. Sledujúc jav zo vzťažnej sústavy viazanej na Zem, voda rieky pôsobí zotrvačnou silou na pravý breh, v smere zrýchlenia na obrázku vyznačeného zelenou farbou. Zo vzorca vyplýva, že na južnej pologuli rieky viac vymieľajú ľavý breh.

____________________________________

Príklad 2.2.2.1: Dievča s hmotnosťou m stojí na váhach, ktoré sú umiestnené v kabíne výťahu. Rozhodnite, či váha ukážu rovnakú výchylku, ak výťah a) je v kľude, b) rozbieha sa so zrýchlením a smerom nahor c) pohybuje sa so spomalením a smerom nahor, d) pohybuje sa so zrýchlením a smerom nadol, e) so spomalením a smerom nadol. Kedy bude dievča relatívne najspokojnešie so svojou hmotnosťou, ak dbá o svoju štíhlu líniu?

Riešenie:

a) Výťah v pokoji predstavuje inerciálny systém, v ktorom jedinou pôsobiacou silou je tiažová sila . Ak si zvolíme súradnicovú sústavu s osou z orientovanou smerom nadol, pôsobiaca tiaž v tejto sústave je určená G = (0,0,G) . Váhy v pokoji ukážu výchylku, odpovedajúcu tiaži dievčaťa G = mg.

b) Ak sa výťah pohybuje so zrýchlením a , jedná sa o neinerciálny vzťažný systém. Ak v ňom chceme uplatniť Newtonovu pohybovú rovnicu musíme k skutočnej tiažovej sile pripočítať sily zotrvačné. Počas pohybu výťahu so zrýchlením a vzniká dodatočná príťažlivá sila smerom opačným ako zrýchlenie, ktoré ju vyvolalo. Pohybová rovnica vo vektorovom tvare pre neinerciálny systém bude ma = G + F₀ Sila_. zotrvačnosti (dodatočná príťažlivá sila) a zemská príťažlivosť majú smer v jednej priamke. V prípade pohybu výťahu so zrýchlením a smerom nahor, bude zotrvačná sila smerom nadol F₀ = (0,0, a ). Vektorová pohybová rovnica prejde na skalárny tvar m a´ = mg + ma = m(g + a) .Váha ukáže väčšiu výchylku, zväčšenú práve o súčin ma.

c) V prípade pohybu so spomalením a smerom nahor, vektor zrýchlenia neinerciálnej sústavy má smer nadol, takže F₀ = (0,0, - ma ), a pohybová rovnica prejde na tvar m a = mg - m a = m( g - a) .Váha ukáže menšiu výchylku práve o súčin ma vzhľadom na výchylku váh v stave, keď výťah je v kľude.

d) V prípade keď výťah sa pohybuje so zrýchlením a smerom nadol, dodatočná príťažlivá sila zotrvačnosti

má smer opačný t.j. F₀ = (0,0, - m a) a pohybová rovnica bude m a = m a - m a = m( g - a). Váha ukáže

opäť menšiu výchylku práve o súčin m a..

d) V prípade pohybu výťahu so spomalením a smerom nadol, vektor zrýchlenia neinerciálnej sústavy má smer nahor, takže dodatočná príťažlivá sila zotrvačnosti je F₀ = (0,0, m a). Pohybová rovnica má tvar m a = mg + ma = m( g + a) ..Váha ukáže väčšiu výchylku odpovedajúcu práve súčinu m a.. Dievča, ktoré dbá o svoju štíhlu líniu, bude „ relatívne“ najspokojnejšie so svojou hmotnosťou m, ak sa bude vážiť buď v brzdiacom výťahu smerom nahor resp. v rozbiehajúcom sa výťahu smerom nadol. V obidvoch prípadoch váhy ukážu menšiu hodnotu, ktorá od skutočnej tiaže mg sa zmenší o dodatočnú tiaž m a. V týchto prípadoch všetky telesá, ktoré sú vo výťahu, akoby boli ľahšie. Čím väčšie je zrýchlenie výťahu, tým väčšia je strata tiaži.

__________________________________

Príklad 2.2.2.2 Fyzikálne vysvetlite pozorované zmeny pohybového stavu chlapca stojaceho v autobuse, ktorý sa rozbieha so zrýchlením resp., ktorý brzdí. Svoje úvahy graficky znázornite.

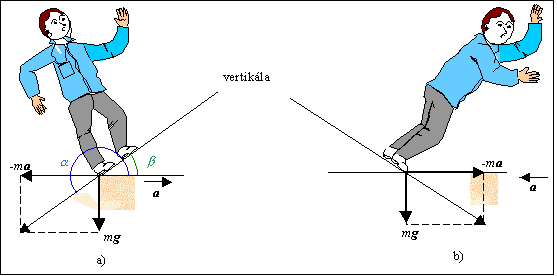
Riešenie: Zrýchlene pohybujúci sa autobus je neinerciálny vzťažný systém. Ak chceme riešiť pohybovú rovnicu musíme ku skutočnej tiažovej sile zvážiť i sily zotrvačné. Jedinou zotrvačnou silou je, opäť ako v prípade výťahu, postupná zotrvačná sila, ktorá má však smer kolmý na zemskú príťažlivosť. To vyvoláva zvláštne pocity u každého cestujúceho. Ak autobus sa rozbieha so zrýchlením a (obr. a), vzniká dodatočná sila, ktorá má opačný smer ako zrýchlený pohyb autobusu. Zložíme túto silu s príťažlivou silou Zeme. Na chlapca, ktorý je v autobuse, bude pôsobiť sila, ktorá so smerom pohybu zviera tupý uhol (a ) . Keď chlapec stojí tvárou v smere pohybu, cíti, že sa autobus pohol. Aby nespadol, musí sa postaviť „vertikálne“. Okamžitá vertikála bude šikmá. Chlapcova vertikála zviera ostrý uhol (b) so smerom pohybu. Ak chlapec bude stáť a nebude sa niečoho držať, určite spadne dozadu. Ak autobus brzdí (obr. b), chlapcova vertikála sa nakláňa dozadu. Chlapcovi v okamžiku začiatku brzdenia sa zdá, že ho niekto strčil do chrbta (vertikálu má za chrbtom). V takejto polohe však nezostáva nadlho. Autobus zastavuje, spomalenie sa stráca a „vertikála“ prechádza do pôvodného stavu. Treba opäť meniť polohu tela. Chlapec sa narovná. Má pocit akoby ho niekto strčil do hrude.

Príklad 2.2.2.3: Rozhodnite, či tiaž telesa na póle a na rovníku je rovnaká. Svoje tvrdenie fyzikálne zdôvodnite. Určite o koľko je ľahšie kilogramové závažie na rovníku ako na póle za predpokladu, že Zem má presne tvar gule o polomere R.

Riešenie: Telesá nachádzajúce sa na rôznych miestach zemského povrchu sa nachádzajú v rôznych vzdialenostiach od osi Zeme, čo závisí od jeho zemepisnej šírky. Pri prechode od pólu k rovníku sa táto vzdialenosť zväčšuje. Odstredivá sila je určená

a_od = - w ´ (w ´ r´) .

Ak si vyjadríme uhlovú rýchlosť otáčania Zeme w pomocou počtu otáčok za jednotku času f, pre veľkosť odstredivého zrýchlenia platí vzťah

a_od = 4 p² f² r´.

Teleso na póle je na osi otáčania, takže r´ = 0 a odstredivé zrýchlenie je rovné nule. Na póle zotrvačná odstredivá sila nepôsobí. Tiaž telesa na póle je určená len silou mg. Odstredivá zotrvačná sila sa pri prechode od pólu k rovníku zväčšuje, pretože sa zväčšuje vzdialenosť telesa od osi rotácie. Na rovníku je odstredivá sila maximálna. Odstredivá sila má smer pozdĺž polohového vektora r´ . Označme si G_r tiaž, ktorú nameriame na rovníku.

G_r = mg_r = m (g - a_od) = m (g - 4 p² f² R).

Zmena tiaže na rovníku bude pre teleso o hmotnosti m

D G = G - G_r = m 4 p² f² R.

Po číselnom vyjadrení dostaneme pre zmenu tiaže kilogramového závažia D G = 0,033778 N

Pozn. V skutočnosti stráca kilogramové závažie ešte viac, pretože Zem je elipsoid (sploštená guľa). Vzdialenosť od pólu do stredu Zeme je menšia ako polomer Zeme na rovníku, priemerne o 1/300 jeho veľkosti.

Kontrolné otázky

1. Vysvetlite pojem sily fiktívne resp. zotrvačné a uveďte ich príklad.

2. Zapíšte rovnicou Coriolisovú silu a vysvetlite jej význam.

3. Kedy vzniká Coriolisová sila? Uveďte konkrétne príklady a  niektoré dôsledky jej pôsobenia.

4. Napíšte matematicky zotrvačnú odstredivú silu. V ktorých systémoch sa s ňou stretávame?

5. Pri pohybe výťahu máme niekedy zvláštne pocity v žalúdku. Viete vysvetliť ich príčinu?

6. Prečo strácame rovnováhu, ak stojíme v rozbiehajúcom sa, alebo brzdiacom autobuse?

7. Akým smerom sa budeme pohybovať, v prípade, že sa nedržíme pri jazde autobusom a autobus prudko začne brzdiť?

8. Ak rieka tečie v smere zemského poludníka, vymývajú sa obidva brehy rovnako? Svoju odpoveď fyzikálne zdôvodnite.

9. Ktorý breh riek, tečúcich v smere poludníkov, sa vymýva viac na severnej pologuli a ktorý na južnej pologuli? Zvážte prípad dolného toku rieky Ural , Mississippi, Niger resp. stredný tok Nílu.

10. Ovplyvňuje smer vetrov Coriolisova sila?

11. Stretávajú sa železničiari s ťažkosťami v dôsledku pôsobenia Coriolisovej sily?

12. Aká sila sa vyskytuje pri rotačnom pohybe zotrvačníkov, rotorov, elektromotorov a turbín?

13. Aké sily pôsobia na osoby i telesá vo vozidlách, konajúcich krivočiary pohyb?

14. Aká sila zmenšuje príťažlivú gravitačnú silu?

15. Je možné vymyslieť taký systém, aby sa človek na otáčajúcom sa systéme vedel udržať aj v miestach vzdialených od osi rotácie? Ak áno, ako sa volá?

16. Ako vysvetlíte vírivý pohyb vody pri jej vypúšťaní z umývadla?

17. Vyteká voda z umývadla rovnako na severnej a južnej pologuli? Svoju odpoveď zdôvodnite.