2.1.4 Pohyb po priamke

Pri pohybe po priamke rozlišujeme pohyby s konštantnou rýchlosťou (vektor rýchlosti nemení veľkosť, ani smer), pohyby s konštantným zrýchlením (nemení sa veľkosť ani smer vektora zrýchlenia) a všeobecné pohyby. Tretí prípad nebudeme rozoberať. V prvom, aj v druhom prípade bude cieľom získať vzťahy vyjadrujúce polohu pohybujúcej sa častice, teda jej karteziánske súradnice, ako funkciu času. V druhom prípade pôjde aj o vyjadrenie závislosti rýchlosti od času.

a) Pri pohybe konštantnou rýchlosťou sa vektor rýchlosti v nemení, jeho derivácia podľa času sa rovná nule, nulové je teda zrýchlenie : a = 0 . Takémuto pohybu sa hovorí pohyb rovnomerný. Ak sa nemení vektor rýchlosti v, nemenia sa ani jeho súradnice v _x , v _y a v _z . Pre každú súradnicu rýchlosti platí vzťah typu v _y = Dy / Dt , takže možno napísať vzťahy Dx = v _x Dt , Dy = v _y Dt , Dz = v _z Dt . Vyjadrujú zmenu súradníc x, y, z pri uplynutí časového intervalu Dt . Predpokladajme, že v časovom okamihu t₁ má častica súradnicu x₁ a v okamihu t₂ súradnicu x₂. Časový interval (t₂ - t₁) rozdeľme na mnoho malých intervalov Dt _i (i = 1, 2, ..., n), takže môžeme napísať

(Dx)_i = v _x (Dt)_i . (2.1.4.1)

Sčítaním všetkých prírastkov súradnice v časovom intervale t₂ - t₁ dostaneme jej celkovú zmenu :

(2.1.4.2)

Preto polohu častice v okamihu t₂ vyjadríme vzorcom

x₂ = x₁ + v_x (t₂ - t₁). (2.1.4.3)

Je zvykom označovať súradnicu na začiatku pohybu ako x_o , nie ako x₁ a príslušný čas (časový okamih) nie ako t₁ , ale ako t_o s tým, že sa zvyčajne považuje za nulový, teda t_o = 0. Vzorec (2.1.4.3) zmení potom svoju podobu :

x₂ = x_o + v_x t₂ ,

pričom platí pre ľubovoľný časový okamih t₂ . Preto sa index vynecháva, takže konečná podoba tohto vzorca má tvar

x = x_o + v_x t. (2.1.4.4)

Grafickým znázornením závislosti veľkosti rýchlosti v = v_x (t) od času pri rovnomernom pohybe v smere osi x, je vždy priamka, rovnobežná s časovou osou t ( obr. 2.1.4.1). Smernica tejto priamky resp. tg a, (a je uhol  priamky s osou nezávisle premennej, ktorým je čas t) je nulová, nakoľko a = o resp. 180 ⁰.

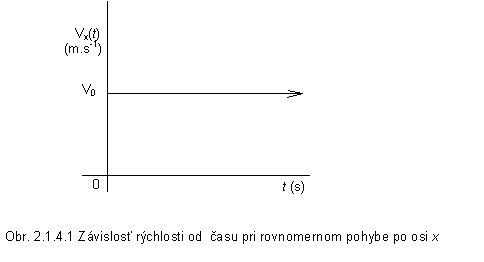
Rovnaké úvahy platia pre obe ďalšie súradnice :

y = y_o + v_y t,

z = z_o +v_z t.

Tieto rovnice vyjadrujú polohu častice pri rovnomernom pohybe po priamke v ľubovoľnom časovom okamihu t. Tieto tri skalárne rovnice postupne vynásobíme príslušnými jednotkovými vektormi i, j, k a sčítame ich ľavé a pravé strany :

(x i + y j + z k) = (x_o i + y_o j + z_o k) + (v_x i +v_y j + v_z k) t,

čo možno prepísať do vektorového tvaru

r = r_o + v t . (2.1.4.5)

V rovnici (2.1.4.2) namiesto sumácie možno integrovať, keď delenie časového intervalu (t₂ - t₁) budeme zjemňovať, takže počet malých časových intervalov (Dt)_i bude rásť nad všetky medze :

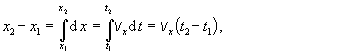(2.1.4.6)

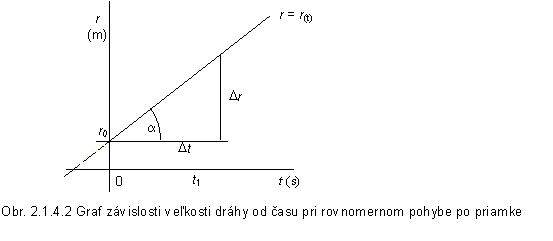
čo nakoniec vedie k rovnakému výsledku, ako je uvedený vo vzorci (2.1.4.4). Grafickým znázornením závislosti veľkosti dráhy x = x( t) od času pri rovnomernom pohybe, určenom vzťahom (2.1.4.6) je priamka ( obr. 2.1.4.2). Smernica tejto priamky resp. tg , kde je uhol  priamky s osou nezávisle premennej, ktorým je čas t, udáva veľkosť rýchlosti skúmaného hmotného bodu.

Vo fyzikálnej literatúre je však zvykom podobne ako pri derivácii, integrovať vektorovú funkciu, takže namiesto troch skalárnych rovníc typu (2.1.4.6) sa píše jedna vektorová rovnica :

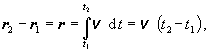(2.1.4.7)

takže po zmene symboliky, spomenutej pred vzorcom (2.1.4.4), dostaneme rovnaký výsledok ako (2.1.4.5) .

Poznámka: Vektory r , r_o a v , vystupujúce vo vzorci (2.1.4.5), nemusia byť rovnobežné, teda nemusia ležať na jednej priamke. Závisí to od voľby vzťažného bodu, teda začiatku súradnicovej sústavy. Ak leží na priamke, všetky uvedené vektory sú s priamkou rovnobežné. Na obr. 2.1.4.3 začiatok súradnicovej sústavy leží mimo priamky.

____________________

Príklad 2.1.4.1. Pozdĺž osi x sa pohybuje častica konštantnou rýchlosťou 5 m.s^-1 smerom k začiatku súradnicovej sústavy, pričom v čase t_o = 0 mala súradnicu x_o = 3 m . Napíšte skalárnu rovnicu pre jej pohyb a vypočítajte: a) kedy príde do začiatku sústavy , b) akú dlhú dráhu prešla.

Riešenie: a) Polohu častice pri pohybe rovnomernom vyjadruje rovnica (2.1.4.5) : r = r_o + v t . Podľa zadania vektory r_o a v  majú opačný smer. Túto rovnicu môžeme napísať aj v tvare

(x i + y j + z k) = (x_o i + y_o j + z_o k) + v t ,

pričom si uvedomujeme, že vektor v  má opačný smer ako jednotkový vektor i . Súradnice y, z, y_o a z_o sú pritom nulové, lebo ide o pohyb po osi x . Keď rovnicu vynásobíme skalárne jednotkovým vektorom i , dostaneme :

x = x_o + (v × i) t = x_o + (v cosp )t = x_o - vt .

Tu si treba uvedomiť, že veličina v  = 5 m/s je veľkosť (absolútna hodnota) vektora rýchlosti, ktorá nemôže byť záporná. Rovnicu (2.1.4.5) možno napísať aj v úplnom zložkovom tvare

(x i + y j + z k) = (x_o i + y_o j + z_o k) + (v _x i + v _y j + v _z k) t ,

takže po jej skalárnom vynásobení jednotkovým vektorom i dostaneme

x = x_o + v _x t .

V tomto prípade však súradnica v _x = - 5 m/s musí byť záporná, aby rovnica správne opisovala pohyb podľa zadania. Z oboch foriem zápisu súradnice x ako funkcie času dostaneme správny výsledok. Okamih t₁ príchodu častice do začiatku súradnicovej sústavy získame z podmienky, že súradnica x sa vtedy rovná nule :

0 = x_o - v . t₁ Þ t₁ = x_o / v = (3/5) s .

b) Vzdialenosť (veľkosť dráhy) s, ktorú častica prešla, vypočítame ako absolútnu hodnotu rozdielu jej súradníc na konci a na začiatku pohybu s = ½x₁ - x_o½ = 3 m .

___________________________________

Poznámka Výsledok z časti b) príkladu 2.1.4.1 poukazuje na rozdiel medzi polohou častice a veľkosťou (dĺžkou) dráhy, ktorú častica prešla. Vzťahy (2.1.4.4) a (2.1.4.5) vyjadrujú polohu častice, nie veľkosť prejdenej dráhy.

b) Pri pohybe s konštantným zrýchlením sa nemení vektor zrýchlenia a , preto jeho derivácia podľa času je nulová. Takémuto pohybu sa hovorí pohyb rovnomerne zrýchlený. Na základe definície ( 2.1.3.1) môžeme napísať dv = a dt a tento vzťah integrovať :

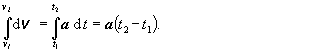(2.1.4.8)

Podobne ako pri rýchlosti, po zmene indexov dostávame rovnicu :

v = v _o + a t. (2.1.4.9)

Táto rovnica vyjadruje závislosť vektora rýchlosti častice od času pri pohybe konštantným zrýchlením. Graf závislosti rýchlosti od času pri rovnomerne zrýchlenom pohybe v smere osi x ukazuje obr. 2.1.4.4.

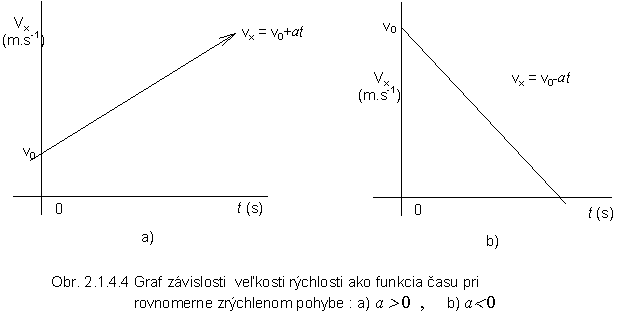
Skutočnosť, že vektor zrýchlenia je konštantný, sa prejavila pri integrovaní v rovnici ( 2.1.4.8) , kde bolo možné vektor zrýchlenia vyňať pred integrál.

Vzťah (2.1.4.9) vyjadruje rýchlosť, pričom polohový vektor častice získame jeho ďalšou integráciou. Uplatníme pritom definíciu vektora rýchlosti v = dr / dt , na základe ktorej napíšeme dr = Cdt , a tento vzťah integrujeme :

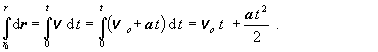(2.1.4.10)

Integrál na ľavej strane rovnice sa rovná r - r_o , takže pre polohový vektor platí

r = r_o + v_ot + a t² /2 . (2.1.4.11)

Poznámky: Je to vektorový vzťah, a vektory v ňom vystupujúce nemusia byť rovnobežné, hoci ide o pohyb po priamke. Treba ďalej zdôrazniť, že v prípade pohybu, pri ktorom sa zrýchlenie s časom mení, tento vzorec neplatí (napr. zrýchlenie auta pri rozbiehaní, štart rakety, ...) . Pozri príklad 2.1.4.3 .

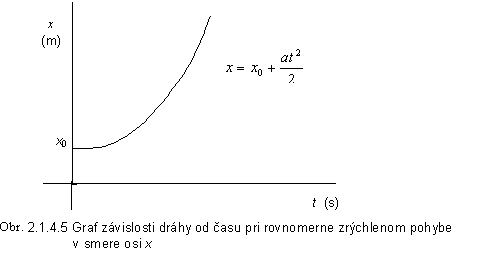
Grafická závislosť dráhy pri rovnomerne zrýchlenom pohybe v smere osi x s nulovou počiatočnou rýchlosťou v₀ znázorňuje graf na obr. 2.1.4.5, ktorý z matematického hľadiska znamená pohyb po parabole.

_________________________

Príklad 2.1.4.2 Stojíme na balkóne vo výške h nad úrovňou terénu. Akou rýchlosťou v_o musíme kameň vyhodiť zvislo nahor, aby na zem dopadol o n sekúnd ?

Riešenie: Na prvý pohľad by sme mali tento prípad riešiť v dvoch etapách - najprv vyriešiť ako vysoko vyletí a koľko mu to bude trvať, potom v druhej etape riešiť prípad ako voľný pád z vypočítanej výšky. Príklad však možno vyriešiť naraz, použitím vzťahu (2.1.4.11) . Ide o pohyb vo zvislom smere, s ktorým stotožníme súradnicovú os y . Rozpíšeme rovnicu (2.1 .4.11) do zložkového tvaru

(x i + y j + z k) = (x_o i + y_o j + z_o k) + (v_ox i + v_oy j + v_oz k) t +

+ (1/2) (a_x i + a_y j + a_z k) t ² ,

vynásobíme jednotkovým vektorom j orientovaným pozdĺž osi y zvislo nahor , takže dostaneme :

y = y_o + v_oy t + (1/2) a_y t ² .

Ak sme kameň vyhodili v okamihu t = 0 , platí y_o = h , v_oy = v_o a veľmi dôležité je uvedomiť si, že a_y = -g , kde g je veľkosť zrýchlenia voľného pádu. Záporné znamienko v tomto prípade znamená, že vektor zrýchlenia voľného pádu má opačný smer ako jednotkový vektor j . Tak dostaneme rovnicu

y = h + v_o t - (1/2) g t ² ,

z ktorej bezprostredne vypočítame rýchlosť v_o z podmienky, že súradnica y pri dopade sa rovná nule :

0 = h + v_o t₁ - (1/2) g t₁² .

V tejto rovnici sú okrem rýchlosti v_o všetky veličiny známe, vrátane okamihu dopadu kameňa t₁ = n sekúnd takže

_____________________________________

Pohyb, pri ktorom je zrýchlenie konštantné, je v prírode i technike viacmenej výnimkou. Zrýchlenie býva komplikovanou funkciou času, takže rýchlosť, alebo polohu častice v danom okamihu už nemožno počítať na základe jednoduchých vzorcov. Pokiaľ je možné závislosť zrýchlenia vyjadriť analytickou funkciou, rýchlosť, i polohu častice možno vypočítať, ako ukazuje nasledujúci príklad.

_________________________________

Príklad 2.1.4.3 Zrýchlenie častice, ktorá sa pohybuje po osi x je dané vzťahom a_x = k₁ - k₂ v_x , kde v_x je súradnica rýchlosti častice a k₁ , k₂ sú kladné konštanty. (Je to reálny prípad, lebo s rastúcou rýchlosťou zrýchlenia ubúda - ako pri jazde autom). Nájdite závislosť zrýchlenia, rýchlosti a polohy častice ako funkcie času, keď v čase t = 0 bola častica v pokoji a nachádzala sa v mieste so súradnicou x = x_o .

Riešenie: Podľa definície platí medzi súradnicami rýchlosti a zrýchlenia vzťah a_x = dv_x / dt , takže môžeme napísať rovnicu :

Po integrácii dostaneme

ln (1 - (k₂ /k₁ ) v_x ) = - k₂ t , resp.

v_x = (1 - exp(-k₂t))×(k₁ /k₂) ,

čo je závislosť rýchlosti od času. Vidno, že pre t ® ¥ rýchlosť dosahuje asymptotickú hodnotu k₁ /k₂ . Deriváciou rýchlosti dostaneme závislosť zrýchlenia od času : a_x = dv_x /dt = k₁ exp(-k₂ t), z ktorého vyplýva, že zrýchlenie sa s rastúcim časom asymptoticky blíži k nule. Obe závislosti - pre rýchlosť aj pre zrýchlenie sú realistické. Pre súradnicu rýchlosti platí definičný vzťah v_x = dx /dt , čo využijeme na výpočet polohy častice :

,

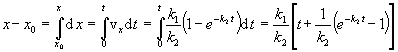z čoho dostaneme výsledok

.

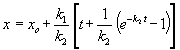Tento výsledok hovorí, že po dostatočne dlhom čase, keď sa rýchlosť už prakticky ustáli, súradnica sa s časom mení lineárne.

_________________________________

Príklad 2.1.4.4 Raketa sa z pokoja začala pohybovať tak, že jej zrýchlenie pri priamočiarom pohybe rovnomerne rastie s časom. Za prvých 5 s pohybu jej zrýchlenie vzrástlo na hodnotu a₁ = 5 m.s^-2. Za predpokladu, že vplyv prostredia na pohyb rakety zanedbáte určite:

a) funkčnú závislosť zrýchlenia rakety od času pri tomto priamočiarom pohybe a smer, v ktorom pohyb prebieha;

b) funkčnú závislosť jej rýchlosti od času pri tomto pohybe;

c) funkčnú závislosť prebehnutej dráhy od času pri tomto priamočiarom pohybe;

d) akú rýchlosť dosiahla za pol minúty svojho pohybu;

e) akú dráhu za tento čas raketa prebehla.

Riešenie: Zo zadania príkladu si vypíšeme veličiny a ich hodnoty, ktoré príklad udáva :

v₀ = v(0) = 0 m.s^-1

t₁ = 5 s

a₁ = 5 m.s^-2

t₂ = 0,5 min = 30 s

a) Určíme funkčnú závislosť zrýchlenia rakety od času pri tomto priamočiarom pohybe.

Prvá veta príkladu hovorí, že strela sa dáva do pohybu takým spôsobom, že jej zrýchlenie pri priamočiarom pohybe rovnomerne rastie s časom. Graficky túto skutočnosť môžeme znázorniť priamkou a matematicky formulovať rovnicou priamky, ktorá je v súradnicovom systéme xy vyjadrená rovnicou y = kx+q. V nami skúmanom prípade nezávisle premennou je čas t a závisle premennou zrýchlenie a. Preto pri transformácii súradníc x® t a y ® a , zvážení, že v okamihu t₀ = 0  raketu umiestnime do začiatku súradnicového systému, časová závislosť zrýchlenia bude daná vzťahom

a = a(t) = a(t) i = kti

Konštantu priamej úmernosti k, resp. smernicu tejto priamky, určíme zo zadaných hodnôt t₁ a zrýchlenia a₁(t₁)

a(t₁) = kt₁ ® k = a(t₁) /t_1. Po dosadení číselných hodnôt dostávame k =1 m.s ^–3.

b) Určime funkčnú závislosť rýchlosti od času pri tomto pohybe:

Keďže sa jedná o pohyb po priamke a začiatok nami zvoleného súradnicového systému leží na tejto priamke, počas celého pohybu bude ležať i vektor rýchlosti v i polohový vektor strely r v smere vektora zrýchlenia a, t.j. v smere určeným jednotkovým vektorom i _. Veľkosť rýchlosti určíme

,

.

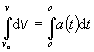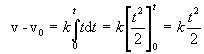Počiatočná rýchlosť v₀ strely je nulová, takže pre hľadanú funkčnú závislosť veľkosti rýchlosti od času dostávame vzťah v(t) = k t² /2.

c) Určime časovú závislosť polohy z definície rýchlosti

.

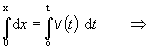
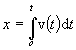Pre veľkosť prebehnutej dráhy (dĺžku) dostávame

.

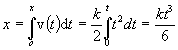d) Určime, akú rýchlosť dosiahla strela za pol minúty svojho pohybu:

Z vypočítanej závislosti rýchlosti od času v(t) =k t²/2 po dosadení uvedených číselných hodnôt dostaneme

v(t₂) = k t₂²/2 = 450 m/s

e) Určime, akú dráhu za tento čas strela prešla:

Z vypočítanej závislosti polohy od času x (t) = kt³/6 , po dosadení uvedených číselných hodnôt, dostaneme pre dĺžku ubehnutej dráhy ½x-x₀½= 4 500 m.

__________________________________________________

Príklad 2.1.4.5 Určite okamžité rýchlosti objektu v bodoch A ,V a M, ak časová závislosť pohybu v smere osi x je určená grafom na obrázku.

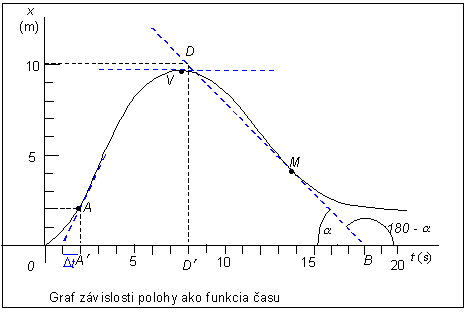
Riešenie: Keďže nemáme zadanú exaktnú rovnicu závislosti x ako funkciu času t, nemôžeme dať precíznu odpoveď, pretože nepoznáme (dx / dt )_A resp. v bodoch V a M. Odpovedať na otázku nám pomôže nákres dotyčnice ku grafu funkcie v danom bode. Smernica dotyčnice v tomto bode určuje okamžitú rýchlosť objektu v skúmanom bode grafu.

_.

Po číselnom dosadení hodnôt odčítaných z grafu dostaneme v _A = 2 ms^-1. Bod V je maximom funkcie x = x(t). Dotyčnica v tomto bode je rovnobežná s časovou osou, t.j. smernica resp. derivácia funkcie v bode V sa rovná nule . Objekt sa v bode V zastaví.

Obdobne určíme okamžitú rýchlosť v bode M z trojuholníka B D D¢.

.

Záporné znamienko hovorí, že objekt sa pohybuje v zápornom smere osi x .

__________________________________

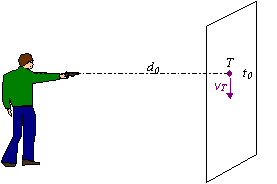
Príklad 2.1.4.6 Na strelnici v lunaparku chce strelec zasiahnuť nábojom vystreleným z pušky pohyblivý terč T. Predpokladajme, že náboj sa pohybuje rovnomerným priamočiarym pohybom s  rýchlosťou v_n = 50 m.s^-1. Terč v okamihu výstrelu sa nachádza vo vertikálnej rovine v bode T vo vzdialenosti d₀ = 3 m od strelca a pohybuje sa kolmo na túto spojnicu rovnomerným priamočiarym pohybom rýchlosťou v_T = 20 m.s^-1. Zistite, či strelec zasiahol terč, ak mieril pod uhlom 30 ⁰ od  horizontálnej roviny ( viď obrázok).

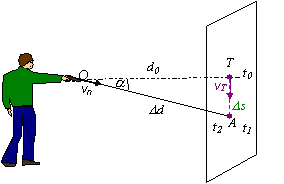
Riešenie: Aby strelec trafil terč, musí sa terč i strela v určitom časovom okamihu t nachádzať na rovnakom mieste, ktoré označíme A. Nech sa terč z bodu T do bodu A dostane za časový interval D t₁ = t₁ – t₀ (t₀ = 0 ) a za tento interval prebehne dĺžku dráhy Ds, určenej rovnicou

. (a)

Z obrázku pre miesto zásahu platí

_. (b)

Dobu letu terču určíme, ak dosadíme rovnicu (b) do (a)

Označme t₂ dobu letu náboja z bodu O do bodu A.  Za túto dobu náboj preletí dĺžku dráhy Dd, pre ktorú platí

.

Na základe Pythagorovej vety a po dosadení za Dd, určíme časový interval t₂ potrebný na doletenie náboja do bodu A.

.

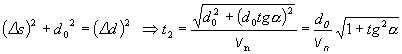Ak náboj i terč doletia do bodu A za rovnaký časový interval, strelec trafí terč. Po dosadení číselných hodnôt dostávame pre

,

_.

Získané číselné hodnoty sú rôzne, takže strelec nezasiahol pohyblivý terč.

___________________________________

Kontrolné otázky

1. Z hľadiska akých dvoch fyzikálnych veličín možno klasifikovať pohyb? Definujte tieto veličiny a urobte klasifikáciu pohybov.

2. Vyjadrite časovú závislosť dráhy pre pohyb priamočiary rovnomerne zrýchlený so zrýchlením a, ktorého začiatočná rýchlosť bola nenulová. Zvážte možné prípady.

3. Nakreslite grafickú závislosť rýchlosti hmotného bodu ako funkciu času, ak sa hmotný bod pohybuje priamočiaro v smere osi x : a) rovnomerne , b) rovnomerne zrýchlene.

4. Nakreslite grafickú závislosť zrýchlenia hmotného bodu ako funkciu času, ak sa hmotný bod pohybuje priamočiaro v smere osi y : a) rovnomerne , b) rovnomerne zrýchlene.

5. Nakreslite grafickú závislosť polohy hmotného bodu ako funkciu času, ak sa hmotný bod pohybuje priamočiaro v smere osi x : a) rovnomerne , b) rovnomerne zrýchlene.

6. Napíšte rovnicu trajektórie častice, ktorú spustíme v gravitačnom poli Zeme a) s nulovou počiatočnou rýchlosťou, b) s nenulovou počiatočnou rýchlosťou z výšky y₀ nad Zemou.

7. Aký pohyb koná teleso vrhnuté zvisle nahor s nenulovou počiatočnou rýchlosťou?

8. Aký pohyb koná častica, ktorá v ľubovolných, ale rovnakých časových intervaloch, prejde rovnaké dráhy?