2.1.2 Rýchlosť

Pod rýchlosťou bežne rozumieme dráhu ubehnutú za jednotku času. Presnejšia definícia hovorí, že ide o podiel ubehnutej dráhy a príslušného časového intervalu : Ds /Dt . Preto sa rýchlosť meria v jednotkách m/s, alebo km/h . Podielom v_p = Ds /Dt určujeme priemernú rýchlosť (napríklad vlak z Trnavy do Žiliny, keď do vzorca dosadzujeme vzdialenosť miest a cestovnú dobu, počas ktorej vlak sa pohyboval rôznou rýchlosťou). V rôznych technických a fyzikálnych aplikáciách je však potrebné poznať rýchlosť v danom okamihu. Okrem toho takouto definíciou by sme nezohľadnili vektorovú povahu rýchlosti. Preto sa rýchlosť zavádza ako derivácia polohového vektora podľa času, čiže ako limita podielu :

(2.1.2.1)

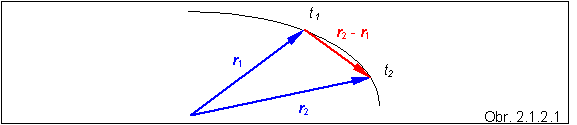
V čitateli zlomku je rozdiel polohových vektorov vyjadrujúcich polohu pohybujúcej sa častice v okamihoch t₁ a t₂ (obr. 2.1.2.1). Rozdiel vektorov r₂ – r₁ určuje smer vektora rýchlosti. V limite, keď sa okamihy t₁ a t₂ vzájomne približujú, budú sa k sebe približovať koncové body vektorov r₂ a r₁ , a vektor r₂ – r₁ sa bude približovať k dotyčnici čiary, po ktorej sa častica pohybuje. Tento rozdiel podľa definície ešte násobíme skalárom 1/(t₂ - t₁), ktorý už nezmení smer vektora r₂ – r₁ , len jeho veľkosť. Preto definícia podľa vzorca (2.1.2.1) určuje veľkosť, tak smer vektora rýchlosti.

Polohový vektor má tri zložky, r(t) = x(t) i + y(t) j + y(t) j , takže jeho deriváciu možno vyjadriť ako súčet derivácií jeho zložiek :

(2.1.2.2)

S vektormi i , j , k pri derivovaní počítame ako s konštantami, lebo v našej súradnicovej sústave sa nemenia. Z posledného vzorca vidno, že

(2.1.2.3)

Pre veľkosť vektora rýchlosti platí vzťah :

(2.1.2.4)

Treba si ešte pripomenúť, že vektor rýchlosti možno vyjadriť aj ako skalárny násobok jednotkového vektora t , teda ako v = vt .

Kontrolné otázky

1. Definujte priemernú rýchlosť.

2. Definujte okamžitú rýchlosť hmotného bodu.

3. Vyjadrite vektor rýchlosti v zložkovom tvare.

4. Vyjadrite vektor rýchlosti v ako súčet priemetov vektora v do jednotlivých osí karteziánskej súradnicovej sústavy.

5. Napíšte vzťah pre veľkosť vektora rýchlosti.

6. Aký smer má vektor rýchlosti?