2.1.10 Zložený pohyb - rýchlosť

V niektorých situáciách je vhodné opisovať pohyb častice (telesa) sprostredkovane, pomocou inej súradnicovej sústavy, vzhľadom na ktorú sa častica pohybuje jednoduchším spôsobom. Napríklad pohyb súčiastky po otáčajúcom sa ramene robota, alebo obiehanie družice okolo Mesiaca, ak ho chceme vyjadriť vzhľadom na sústavu viazanú na Zem. Cieľom bude vyjadriť polohu, rýchlosť a zrýchlenie častice v takomto zložitejšom prípade.

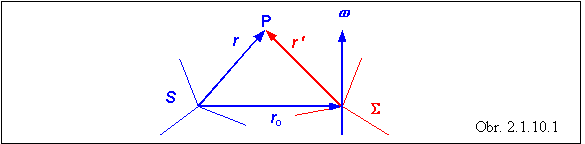
Budeme opisovať pohyb častice ( nachádza sa v bode P) vzhľadom na inerciálnu súradnicovú sústavu S a súčasne vzhľadom na neinerciálnu sústavu S podľa obrázku 2.1.10.1 .

Poznámka: S definíciou pojmov inerciálna a neinerciálna sústava sa oboznámime v druhej podkapitole. Neinerciálna sústava je taká sústava , ktorá nekoná rovnomerný priamočiary pohyb.

Polohový vektor bodu P vzhľadom na sústavu S je označený písmenom r , vzhľadom na sústavu S písmenom r ¢ , polohový vektor začiatku sústavy S vzhľadom na sústavu S je označený písmenom r_o . Sústava S sa otáča uhlovou rýchlosťou w vzhľadom na sústavu S , takže je neinerciálna. Medzi polohovými vektormi bodu P platí vzťah

r = r_o + r ¢, (2.1.10.1)

Pritom vektory r a r_o vyjadrujeme pomocou jednotkových vektorov i , j , k  sústavy S , zatiaľ čo vektor r ¢ pomocou jednotkových vektorov i ¢ , j ¢ , k ¢ sústavy S . Preto ich vyjadrenie pomocou súradníc má takýto tvar :

r = xi + yj + zk ,

r_o = x_o i + y_o j + z_ok , (2.1.10.2)

r¢ = x¢ i ¢ + y ¢ j ¢ + z ¢ k ¢.

Rýchlosť častice vzhľadom na sústavu S získame deriváciou vzťahu (2.1.10.1) podľa času. Derivujeme pravú i ľavú stranu rovnice, obe strany z pohľadu sústavy S . Deriváciou ľavej strany dostaneme rýchlosť v , ktorou sa častica pohybuje vzhľadom na sústavu S . Na pravej strane derivujeme dva členy. Deriváciou polohového vektora r_o získame rýchlosť v _o začiatku súradnicovej sústavy S , ktorou sa pohybuje vzhľadom na sústavu S . Pri derivácii vektora r ¢ najprv zvážime, ako ho treba derivovať z hľadiska sústavy S :

(dr ¢/dt)_S = d (x¢ i ¢ + y¢ j ¢ + z¢ k¢) / dt = (dx¢ /dt)i¢+ (dy¢ /dt)j¢ + (d¢z /dt)k¢ = v _x¢i ¢ + v _y' j ¢ +v _z¢k¢.

Výsledok označíme

(dr ¢/dt)_S = v ¢ . (2.1.10.3)

Derivácia polohového vektora r¢, vykonaná vzhľadom na sústavu S , je komplikovanejšia. Sústava S sa vzhľadom na sústavu S otáča, a spolu s ňou i jednotkové vektory i ¢ , j ¢ , k ¢ , čo treba pri derivácii polohového vektora r ¢ zohľadniť. Výrazy typu x¢ i ¢ musíme preto derivovať ako súčin, lebo vzhľadom na sústavu S sa s časom menia oba jeho členy. Súradnica x¢ pri pohybe častice mení svoju veľkosť, a jednotkový vektor i ¢ sa otáča uhlovou rýchlosťou w , takže

di ¢ /dt = w ´ i ¢ .

Preto :

(dr ¢/dt)_S = d (x¢ i¢ + y¢ j' + z' k' ) / dt =

= [(dx' /dt)i' + x' (di' /dt)] + [(dy' /dt)j' + y' (dj' /dt)] + [(dz' /dt)k' + z' (dk' /dt)] =

= [(dx' /dt)i' + (dy' /dt)j' + (dz' /dt)k' ] + [x' (di' /dt) + y' (dj' /dt) + z' (dk' /dt)] =

= [ v _x' i' + v _y' j' + v _z' k' ] + [x' (w ´ i' ) + y' (w ´ j' ) + z' (w ´ k' )] =

= v ' + w ´ (x' i' + y' j' + z' k' ) = v ' + (w ´ r ' ). (2.1.10.4)

Deriváciou rovnice 2.1.10.1 tak dostaneme výsledok

v = v_o + v ' + (w ´ r ' ) . (2.1.10.5)

Podľa tejto rovnice rýchlosť v častice vzhľadom na inerciálnu sústavu možno vypočítať ako súčet troch rýchlostí - rýchlosti začiatku vzťažnej sústavy S vzhľadom na sústavu S , rýchlosti v' častice vzhľadom na sústavu S a tretej rýchlosti, zohľadňujúcej otáčanie sústavy S uhlovou rýchlosťou w .

Druhým významným výsledkom vyplývajúcim zo vzorcov (2.1.10.3) a (2.1.10.4) je vzťah medzi deriváciami vektora r ¢ z hľadiska sústavy S a z hľadiska sústavy S . Porovnaním vzorcov dostaneme :

(dr '/dt)_S = (dr '/dt)_S + (w ´ r ¢) , (2.1.10.6)

čomu sa hovorí vzťah mezi absolútnou a relatívnou deriváciou. Tento vzťah sa týka každého vektora (nie iba polohového), vyjadreného v neinerciálnej otáčajúcej sa sústave S , ak ho derivujeme vzhľadom na inerciálnu sústavu S .

___________________________

Príklad 2.1.10.1 Vyjadrite rýchlosť cestujúceho v električke vzhľadom na koľajnice, keď električka sa pohybuje po priamej trati rýchlosťou v _o a cestujúci v električke kráča smerom k zadnej časti električky rýchlosťou v ' .

Riešenie Sústavu S viažeme na koľajnice, sústavu S na električku. Električka sa neotáča, takže w = 0 . Zo zadania vyplýva, že vektor v ' má opačný smer ako vektor v _o , takže rovnica (2.1.10.5) v skalárnom tvare poskytuje vzťah v = v_o - v ' . Preto rýchlosť cestujúceho vzhľadom na koľajnice je menšia než rýchlosť električky.

___________________________

Poznámka Na predošlom príklade sme si overili, že vzorec (2.1.10.5) poskytuje očakávaný výsledok, že teda opisuje aj jednoduché prípady. Pri používaní tohto vzorca treba vždy starostlivo zvážiť vzájomný smer vektorov, ktoré v ňom vystupujú.

________________________________________

Príklad 2.1.10.2 Vedľa kolotoča otáčajúceho sa konštantnou uhlovou rýchlosťou w nehybne stojí divák. Vypočítajte rýchlosť stojaceho diváka vzhľadom na otáčajúci sa kolotoč.

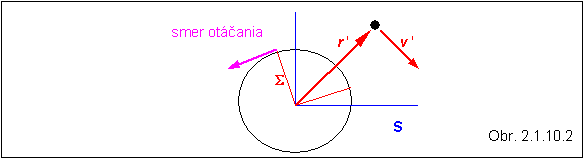
Riešenie: Sústavu S viažeme na otáčajúci sa kolotoč, sústavu S na okolie. Stotožníme začiatky súradnicových sústav, takže r_o = 0 (t.j. r = r ' ) a v _o = 0 . Podľa zadania aj v = 0, takže vzorec ( 2.1.10.5) sa zjednoduší :

0 = v ' + ( w ´ r ' ) ,

alebo

v ' = - (w ´ r ' ) .

Divák sa vzhľadom na kolotoč pohybuje po kružnici. Pri smere otáčania , ako je znázornený na obrázku, vektor uhlovej rýchlosti w smeruje z obrazovky monitora ( resp. z roviny papiera) k nám. Preto vektor v ' má smer, ako je vyznačený na obrázku. Ak sa kolotoč otáča "doľava", divák sa vzhľadom na otáčajúci kolotoč pohybuje po kružnici, pričom sa otáča "doprava" .

_______________________________

Príklad 2.1.10.3 Určite smer a veľkosť rýchlosti súčiastky vzhľadom na podstavec robota, ktorého vodorovné rameno sa otáča uhlovou rýchlosťou w = 0,5 rad/s, pričom súčiastka sa pohybuje pozdĺž ramena rýchlosťou v ' = 10 cm/s smerom od stredu otáčania ramena k jeho okraju.

Riešenie: Pohyb súčiastky pozostáva z dvoch jednoduchých pohybov - z pohybu pozdĺž ramena, čo je pohyb po priamke konštantnou rýchlosťou a z otáčania okolo osi robota konštantnou uhlovou rýchlosťou. Preto inerciálnu sústavu S viažeme na halu, v ktorej sa nachádza robot, pričom začiatok sústavy zvolíme v bode, ktorý je priesečníkom osi robota s rovinou, v ktorej sa otáča rameno. Sústavu S viažme na otáčajúce sa telo robota tak, že začiatky oboch sústav stotožníme. To znamená, že neinerciálna sústava S sa vzhľadom na sústavu S otáča uhlovou rýchlosťou w .

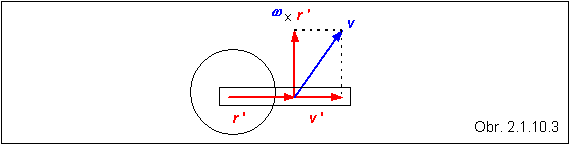
Na výpočet rýchlosti súčiastky v vzhľadom na halu použijeme vzorec (2.1.10.5) :

v = v _o + v ' + (w ´ r ' ) ,

v ktorom rýchlosť v _o = 0 , lebo začiatky sústav sú totožné, teda vzhľadom na seba sa nepohybujú. Rýchlosť v' smeruje pozdĺž ramena, má teda v každom okamihu jeho smer , jej veľkosť je určená v zadaní príkladu. Vektor (w ´ r ' ) má smer kolmý na rameno robota (ako vyplýva z definície vektorového súčinu) a veľkosť w r ' , kde r ' je vzdialenosť súčiastky od stredu otáčania v danom okamihu. Táto vzdialenosť sa pri pohybe súčiastky zväčšuje a keďže ide o pohyb rovnomerný, možno napísať

r ' = v' t + r_o' ,

kde r_o' vyjadruje polohu súčiastky v okamihu t = 0 . Vektor rýchlosti v vzhľadom na sústavu S je zobrazený na obrázku, otáča sa spolu s ramenom robota, mení teda svoj smer . Mení aj svoju veľkosť, ktorú vypočítame podľa Pythagorovej vety :

(2.1.10.7)

Do tohto výsledného vzorca môžeme dosadiť číselné hodnoty a zvoliť si časový okamih, v ktorom chceme rýchlosť vypočítať.

________________________________

Príklad 2.1.10.4 Bod sa pohybuje v inerciálnej sústave S po priamke konštantnou rýchlosťou v . Posúďte pohyb tohto bodu zo sústavy S , ktorá sa vzhľadom na sústavu S otáča uhlovou rýchlosťou w , ale nevzďaľuje sa od nej. Vektor v nech je pre jednoduchosť kolmý na vektor w .

Riešenie : Stotožníme začiatky sústav, takže r_o = 0 , v _o = 0 . Bod sa v sústave S pohybuje konštantnou rýchlosťou, takže r = r₁ + v t . Rýchlosť bodu vzhľadom na S vypočítame pomocou rovnice (2.1.10.5) :

v ’ = v - (w ´ r ) = v - [w ´ (r₁ + v t )],

v ktorej sme využili okolnosť, že r = r ' a vzťah platný pre rovnomerný pohyb r = r₁ + v t . Z tohto výsledku vyplýva, že smer vektora v¢ sa s časom mení, lebo člen (w ´ r ) , špeciálne jeho časť w ´ v t , ktorá je na vektor v kolmá, sa s pribúdajúcim časom zväčšuje.

____________________________________________

Kontrolné otázky

1. Z akých pohybov sa skladá zložený pohyb?

2. Koná dažďová kvapka zložený pohyb ak: a) nefúka vietor, b) ak fúka silný bočný vietor?

3. Kedy hovoríme o derivácii fyzikálnej veličiny absolútnej?

4. Kedy hovoríme o derivácii fyzikálnej veličiny relatívnej?

5. Napíšte súvis medzi absolútnou a relatívnou deriváciou zvolenej fyzikálnej veličiny.

6. Sú jednotkové vektory karteziánskej súradnicovej sústavy vždy konštantné?

7. Z akého dôvodu musíme rozlišovať deriváciu absolútnu a relatívnu?

8. Napíšte vzťah pre deriváciu jednotkového vektora, ktorého veľkosť je konštantná, ale smer sa mení.

9. Vyjadrite rýchlosť hmotného bodu A vzhľadom na absolútnu sústavu. Vysvetlite význam jednotlivých veličín i členov.

10. Vyjadrite rýchlosť hmotného bodu A vzhľadom na relatívnu sústavu. Vysvetlite význam jednotlivých veličín i členov.