1.4.1 Integrácia
podľa času
Najjednoduchším prípadom integrácie vektorovej funkcie je integrál typu
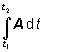 (1.4.1.1)
(1.4.1.1)
v ktorom t je skalárna premenná, pričom vektorová funkcia A závisí od tejto premennej. Keď vektorovú funkciu A(t) rozpíšeme v zložkovom tvare, A = Axi + Ayj + Azk , integrál (1.4.1.1) môžeme rozpísať na tri integrály skalárnych funkcií :
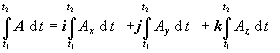
![]() (1.4.1.2)
(1.4.1.2)
Výsledkom je vektorová funkcia, závisiaca od premennej t . Príkladom je impulz sily, definovaný ako integrál sily podľa času :
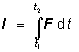 .
.
______________________________________
Príklad 1.4.1.1
Zrýchlenie častice je zadané vzťahom
a = 2t2 i
- 4t j , pričom v čase t
1 mala častica rýchlosť v 1 = 3 j
. Vypočítajte rýchlosť v2
častice v čase t 2 > t 1 keď vieme, že medzi zrýchlením a rýchlosťou
platí vzťah
![]()
![]()
Rýchlosť
meriame v jednotkách m/s, zrýchlenie
v m/s2 .
Riešenie
:
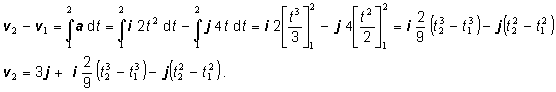
_________________________________________
Kontrolné
otázky
1.
Výsledkom
integrácie vektorovej funkcie podľa času je - vektorová, alebo skalárna
funkcia?
2.
Ak integrujeme
vektorovú funkciu podľa času - môže mať výsledná funkcia iný počet zložiek ako
pôvodná ?
3.
Uveďte
príklad integrácie vektorovej funkcie podľa času !
4.
Pri
integrácii vektorovej funkcie podľa času - majú pôvodná a výsledná funkcia
rovnaký fyzikálny rozmer ?